< Curent alternativ

11 Factorul de putere

11.1 Puterea în circuitele de curent alternativ rezistive şi reactive

Să considerăm un circuit monofazat de curent alternativ, compus dintr-o sursă de tensiune de 120 V, la frecvenţa de 60 Hz, şi o sarcină rezistivă:

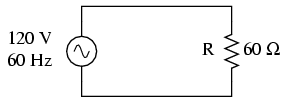
Curentul efectiv prin sarcină va fi de 2 A, iar puterea disipată de 240 W. Deoarece sarcina este pur rezistivă (fără reactanţă), curentul este în fază cu tensiune, iar calculele sunt asemănătoare unui circuit de curent continuu. Formele de undă ale tensiunii, curentului şi puterii, arată asfel:

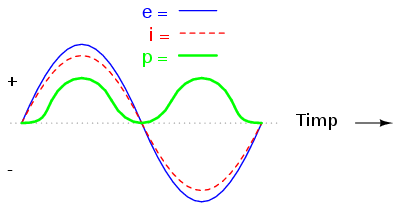
Puterea este tot timpul pozitivă în acest caz. Acest lucru înseamnă că puterea este tot timpul disipată de sarcina rezistivă şi nu este reintrodusă în circuit, aşa cum este cazul sarcinilor reactive.

De asemenea, frecvenţa formei de undă a puterii este dublul frecvenţei tensiunii şi curentului. Această diferenţa de frecvenţă face imposibilă exprimarea puterii în circuitele de curent alternativ folosind aceeiaşi notaţie complexă, rectangulară sau polară, folosită în cazul tensiunii, curentului şi a impedanţei, deoarece această formă de exprimare matematică presupune o frecvenţă constantă pentru toate formele de undă implicate.

Cea mai bună metodă de calcul a puterii în circuitele de curent alternativ se realizează folosind notaţia scalară, iar relaţiile de fază sunt evidenţiate cu ajutorul trigonometriei.

Ca şi comparaţie, să considerăm un circuit simplu cu o sarcină reactivă:

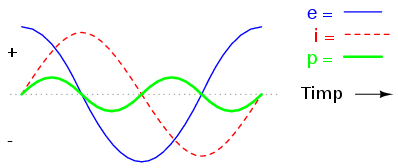
În acest caz, puterea variază alternativ între partea pozitivă şi cea negativă. Acest lucru înseamnă că puterea este alternativ absorbită şi eliberată din şi în circuit. Dacă am considera sursa ca fiind un generator mecanic, practic, energia consumată pentru acţionarea arborelui ar fi zero, deoarece sarcina nu consumă deloc putere.

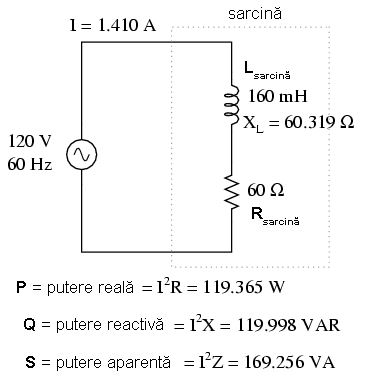
Să considerăm acum un circuit cu sarcină rezistiv-inductivă:

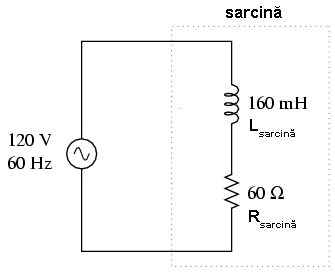
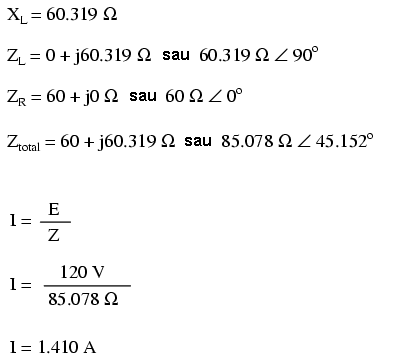
Aceasta este valoarea efectivă a curentului (1.41 A) pe care ar arăta-o un ampermetru conectat în serie cu rezistorul şi bobina. Graficul formelor de undă arată în acest caz asfel:

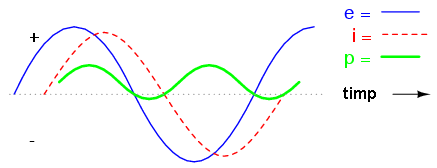
Şi în acest caz, puterea alternează între partea negativă şi cea pozitivă, dar valoarea puterii „pozitive” este mai mare decât cea negativă. Cu alte cuvinte, combinaţie serie rezistor-bobină, va consuma mai multă putere decât va introduce înapoi în circuit.

11.2 Puterea reală, reactivă şi aparentă

Se ştie că elementele reactive precum bobinele şi condensatoarele nu disipă putere, dar existenţa căderii de tensiune şi curentului la bornele lor, dă impresia că acestea ar disipa putere. Această „putere nevăzută” poartă numele de putere reactivă, iar unitatea sa de măsură este Volt-Amper-Reactiv, VAR, şi nu Watt-ul. Simbolul matematic pentru puterea reactivă este „Q”. Puterea reală disipată, sau consumată, dintr-un circuit, poartă numele de putere reală, unitatea sa de măsură este Watt-ul, iar simbolul matematic este „P”. Combinaţie dintre cele două puteri, cea reactivă şi cea reală, poartă numele de putere aparentă. Unitatea de măsură a puterii aparente este Volt-Amper, iar simbolul matematic este „S”.

Ca şi regulă, puterea reală este o caracteristică a elementelor disipative, de obicei rezistori, puterea reactivă caracterizează reactanţa (X) circuitului, iar puterea aparentă depinde de impedanţa (Z) totală a circuitului. Datorită faptului că folosim valori scalare pentru reprezentarea puterilor, toate valorile complexe ale tensiunilor, curenţilor şi impedanţelor trebuie să fie reprezentate sub formă polară şi nu sub formă reală sau rectangulară.

Relaţiile dintre cele trei tipuri de putere şi rezistenţă, reactanţă şi impedanţa (folosind valori scalare), sunt următoarele:

Există două ecuaţii pentru calcularea puterilor reale şi reactive, dar există trei ecuaţii pentru calcularea puterii aparente, P=IE fiind folosită doar în acest scop. Să luăm următoarele circuit pur rezistiv ca şi prim exemplu:

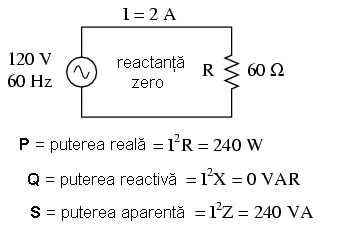
Pentru un circuit pur inductiv (pur reactiv):

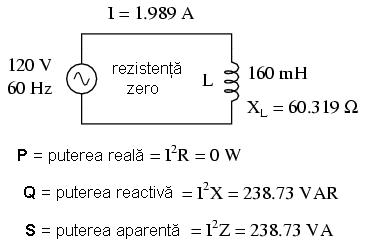
Pentru un circuit rezistiv-inductiv:

Triunghiul puterii

Relaţia dintre cele trei tipuri de putere, reală, reactivă şi aparentă, poate fi exprimată sub formă trigonometrică. Această exprimare este cunoscută sub numele de triunghiul puterii.

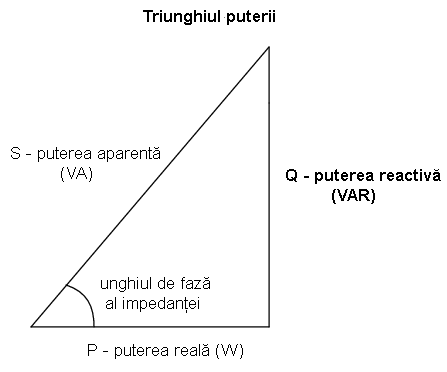
Folosind teorema lui Pitagora, putem afla lungimea oricărei laturi a triunghiului dreptunghic, latură ce reprezintă de fapt puterea respectivă, dacă ştim „lungimile” celorlalte două laturi, sau o lungime şi unghiul de fază din circuit

11.3 Calcularea şi corectarea factorului de putere

Unghiul acestui „triunghi al puterilor” reprezintă raportul dintre valoarea puterii disipate (sau consumate) şi cantitatea de putere absorbită/returnată. De asemenea, reprezintă şi unghiul de fază al impedanţei circuitului, sub formă polară. Acest raport dintre puterea reală şi puterea aparentă poartă numele de factor de putere al circuitului. De asemenea, din geometria triunghiului, putem deduce că factorul de putere este egal şi cu cosinusul unghiului de fază. Folosind valorile din circuitul precedent:

Fiind calculat ca un raport, factorul de putere nu are unitate de măsură.

Pentru circuitele pur rezistive, factorul de putere este 1 (perfect), deoarece puterea reactivă este egală cu zero. În acest caz, triunghiul puterilor este o linie orizontală, deoarece latura opusă (puterea reactivă) va avea lungimea zero.

Pentru circuitele pur inductive, factorul de putere este zero, datorită faptului că puterea reală este zero. În acest caz, triunghiul puterilor este o linie verticală, deoarece latura adiacentă (puterea reală) va avea lungimea zero. Acelaşi lucru este valabil şi pentru circuitele pur capacitive, doar că sensul liniei verticale va fi în jos, nu în sus, cum este cazul circuitelor pur inductive.

Factorul de putere este un element foarte important în proiectarea circuitelor electrice de curent alternativ, deoarece un factor de putere mai mic decât 1 înseamnă că circuitul respectiv, sau mai bine spus, conductorii circuitului în cauză, trebuie să conducă mai mult curent decât ar fi necesar dacă reactanţa circuitului ar fi zero, caz în care, cu un curent mai mic, puterea reală distribuită pe sarcină ar fi aceeiaşi. Un curent mai mare înseamnă secţiuni ale conductorilor mai mari, ceea ce afectează direct costurile realizării instalaţiei electrice. Dacă circuitul considerat mai sus, ar fi fost pur rezistiv, am fi putut transporta o putere de 169.256 W spre sarcină, cu aceeiaşi valoare a curentului de 1.410 A, şi nu doar 119.365 W, valoare ce este disipată în acest moment pe sarcină. Factorul de putere scăzut se traduce printr-un sistem de distribuţie ineficient.

Factorul de putere poate fi însă corectat, paradoxal, prin adăugarea în circuit a unei sarcini suplimentare care să „consume” o cantitate egală de putere reactivă, dar de sens contrar, pentru anularea efectelor reactanţei inductive a sarcinii. Reactanţele inductive pot fi anulate şi cu ajutorul reactanţelor capacitive, şi anume, prin adăugarea unui condensator în paralel cu sarcina (în circuitul precedent). Efectul celor două reactanţe opuse, conectate în paralel, este să aducă impedanţa totală a circuitului la o valoare egală cu cea a rezistenţei totale. Rezultatul reducerea unghiului impedanţei la zero, sau o valoarea cât mai apropiată de zero.

Ştim că puterea reactivă, necorectată, este de 119.998 VAR (inductiv), prin urmare, trebuie să calculăm mărimea corectă a condensatorului, mărime necesară pentru a produce o cantitate egală de putere reactivă (capacitivă). Condensatorul va fi conectat în parelel cu sursa, prun urmare, vom folosi următoarea formulă:

Folosim un condensator cu o capacitate de 22 µF:

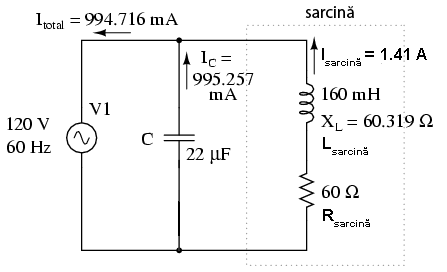
Factorul de putere al circuitului a crescut substanţial, fiind foarte aproape de valoarea 1. Curentul principal a scăzut de la 1.41 A la 994.7 mA, iar puterea disipată pe rezistorul de sarcină a rămas neschimbată, 119.365 W.

Din moment ce impedanţa finală este un număr pozitiv, putem spune că, per total, inductivitatea circuitului este mai mare decât capacitatea sa. Dacă corectarea factorului de putere ar fi fost perfectă, unghiul impedanţei ar fi fost zero, sau pur rezistiv. Dacă în schimb, am fi adăugat un condensator prea mare în paralel, am fi obţinut un unghi al impedanţei negativ, indicând faptul că inductivitatea circuitului este mai mică decât capacitatea sa. Cu un factor de putere de 0.9999, defazajul dintre curent şi tensiune este foarte aproape de 0^o.

Dim moment ce curentul şi tensiunea sunt aproximativ în fază, produsul celor două va da o putere pozitivă pe aproximativ întreaga perioadă. Cu un factor de putere mult sub 1, produsul celor două ar fi fost negativ, fapt ce duce la reintroducerea puterii negative în circuit, înapoi spre generator. Această putere nu poate fi „vândută”, dar circulaţia sa de la sursă la sarcină şi invers, duce la pierderi de putere în lungul liniilor de transport datorită rezistenţei acestora. Conectarea condensatorului în paralel cu sarcina, rezolvă această problemă.

De notat faptul că reducerea pierderilor prin liniile de transport al curentului electric, se aplică doar de la generator la punctul de corecţie a factorului de putere (datorită condensatorului). Cu alte cuvinte, există în continuare circulaţie electrică între condensator şi sarcina (rezistiv-)inductivă. Acest lucru nu este în general o problemă însă, deoarece aplicarea corecţiei factorului de putere se realizează în vecinătatea sarcinii în cauză.

De asemenea, o capacitatea prea mare într-un circuit de curent alternativ va duce la un factor de putere scăzut, la fel ca în cazul unei inductanţe prea mari. Trebuie să fim prin urmare foarte atenţi când realizăm corectarea factorului de putere, pentru a nu supra-corecta circuitul.

11.4 Corectarea practică a factorului de putere

Atunci când avem nevoie de corectarea practică a factorului de putere într-un sistem de putere în curent alternativ, probabil că nu vom fi atât de norocoşi încât să cunoaştem inductanţa exactă a sarcinii. Putem folosi un aparat de măsură special, denumit cosfimetru pentru calcularea factorului de putere. Puterea aparentă o putem calcula folosind un voltmetru şi un ampermetru. În cel mai rău caz însă, am putea fi nevoiţi să folosim un osciloscop pentru calcularea diferenţei de fază, în grade, între formele de undă alte tensiunii şi ale curentului; factorul de putere va fi cosinusul acelui unghi.

Dacă avem acces la un wattmetru pentru măsurarea puterii reale, putem compara valoarea citită cu valoarea puterii aparente deduse din produsul tensiunii totale cu a curentului total.