< Curent alternativ
8 Filtre
8.1 Ce este un filtru
În unele cazuri este necesară folosirea unor circuite capabile să filtreze selectiv o anumită frecvenţă, sau un domeniu de frecvenţe, dintr-un circuit ce conţine o combinaţie de frecvenţe (cap. prec.). Un circuit construit special pentru realizarea acestei selecţii a frecvenţelor poartă numele de circuit de filtrare, sau mai simplu, filtru. O aplicaţie populară pentru circuitele de filtrare este în cazul sistemelor audio, unde este necesar ca anumite domenii de frecvenţe să fie amplificate sau înlăturate pentru obţinerea unui sunet de cea mai înaltă calitate şi eficienţă. Un exemplu este folosirea egalizatorului, ce permite selectarea de către utilizator a domeniilor frecvenţelor şi amplitudinile acestora în funcţie de preferinţele acestuia sau de acustica încăperii. Crossover-ele sunt folosite de asemenea pentru blocarea „accesului” anumitor frecvenţe la difuzoare. Un tweeter (difuzor de frecvenţă înaltă) este ineficient atunci când este folosit la reproducerea semnalelor de frecvenţe joase, asfel că este nevoie de conectarea unui crossover între tweeter şi terminalele de ieşire a sistemului audio pentru blocarea semnalelor de frecvenţă joasă; singurele semnale care trec de acest punct sunt doar semnalele de frecvenţă înaltă. Acest lucru duce la creşterea eficienţei sistelor audio, şi prin urmare la o performanţă crescută. Atât egalizatorul cât şi crossover-ul sunt exemple de filtre, concepute special pentru filtrarea anumitor frecvenţe nedorite.
O altă aplicaţie practică a circuitelor de filtrare constă în prelucrarea tensiunilor ne-sinusoidale în circuitele de putere. Unele componente electronice sunt sensibile în prezentă armonicilor surselor de alimentare, prin urmare, este nevoie de prelucrarea acestor forme de undă pentru funcţionarea normală a dispozitivelor electronice. Dacă o tensiune sinusoidală distorsionată se comportă precum o serie de armonici însumate cu frecvenţa fundamentalei, atunci ar trebui să fie posibilă construirea unui circuit de filtrare care să permită doar trecerea fundamentalei, blocând toate celelalte armonici.
În cele ce urmează, vom studia câteva circuite de filtrare elementare, folosind reprezentarea prin diagrame Bode (variaţia amplitudinii faţă de frecvenţă) pentru diferitele filtre considerate. Totuşi, aceste circuite pot fi analizate luând fiecare frecvenţă împarte şi aplicând teorema superpoziţiei, precum în cazul precedent.
8.2 Filtrul trece-jos
Prin definiţie, filtrul trece-jos permite trecerea (impedanţă mică) semnalelor de frecvenţă joasă şi blochează trecerea (impedanţă mare) celor de frecvenţă înaltă.
Filtrul trece-jos inductiv
Există două tipuri de circuite capabile să îndeplinească aceste condiţii, şi multe versiuni din fiecare: filtrul trece-jos inductiv şi filtrul trece-jos capacitiv:
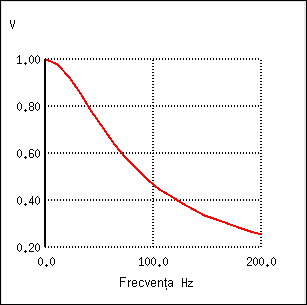
În această configuraţie, impedanţa bobinei creşte odată cu creşterea frecvenţei, iar această impedanţă în serie cu rezistenţa de sarcină (bec, motor electric, ventilator, etc.) face ca semnalele de frecvenţă înaltă să nu ajungă la aceasta (blocarea/filtrarea lor). Grafic, comportamentul filtrului, atunci când este supus unei forme de undă multi-frecvenţă, arată asfel:
Filtrul trece-jos capacitiv
Să considerăm şi filtrul trece-jos capacitiv:
Impedanţa condensatorului scade odată cu scăderea frecvenţei. Acestă impedanţă mică, conectată în paralel cu rezistenţa de sarcină, duce la scurt-circuitarea celei din urmă la semnalele de frecvenţă înaltă, iar mare parte din căderea de tensiune se va regăsi pentru rezistorul serie R1.
Comparaţie între filtrele trece-jos inductive şi capacitive
Filtrul trece-jos inductiv este cât se poate de simplu, constând doar dintr-un singur comonent, bobina. Versiunea capacitivă a aceluiaşi filtru nu este nici ea mai complicată, constând dintr-un rezisotr şi un condensator. Totuşi, filtrele capacitive, chiar dacă sunt puţin mai complexe, sunt cele mai folosite dintre cele două, deoarece condensatoarele sunt în general elemente reactive mai „pure” decât bobinele, prin urmare, comportamentul acestora este mult mai previzibil. Prin pur se înţelege faptul că rezistenţa condensatoarelor este mult mai mică decât cea a bobinelor, fiind asfel aproape 100% reactive. Bobinele, pe de altă parte, prezintă efecte disipative importante (rezistive), atât în lungimea firelor utilizate cât şi prin pierderile magnetice din miezul magnetic. Condensatoarele sunt mult mai puţin supuse efectelor de „cuplaj” cu alte componente şi sunt mult mai ieftine decât bobinele.
Totuşi, filtrul trece-jos inductiv este adeseori preferat în cazul redresării tensiunii de curent alternativ în curent continuu pentru eliminarea vârfurilor create în această situaţie, rezultând o componentă continuă pură. Principalul motiv al alegerii constă în necesitatea unei rezistenţe mici a filtrului pentru ieşirea unei asfel de surse de alimentare. Un filtru capacitiv necesită introducerea unei rezistenţe suplimentare în serie cu sursa, pe când unul inductiv nu. Dacă în circuitul de curent continuu considerat, adăugarea unei rezistenţe suplimentare nu este de dorit, atunci filtrul trece-jos inductiv este cea mai bună alegere pentru filtrarea formei de undă. Pe de altă parte, dacă priorităţile principale sunt un volum şi o greutate scăzută, atunci filtrul capacitiv este cea mai bună alegere.
Frecvenţa de tăiere
Toate filtrele trece-jos au o anumită proprietate, şi anume, frecvenţa de tăiere, şi reprezintă frecvenţa peste care tensiunea de ieşire a circuitului scade sub 70.7% din valoarea tensiunii de intrare. Această valoare de 70.7% nu este arbitrară, chiar dacă pare aşa la prima vedere.
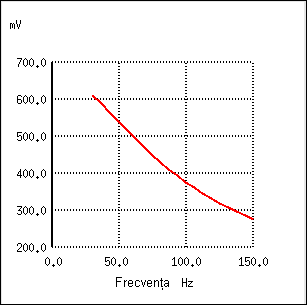
Într-un circuit simplu trece-jos capacitiv sau inductiv, frecvenţa de tăiere reprezintă frecvenţa la care reactanţă capacitivă (în ohmi) este egală cu rezistenţă (în ohmi). Într-un circuit trece-jos capacitiv simplu (un rezistor, un condensator), frecvenţa de tăiere este dată de următoarea formulă:
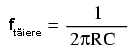
Realizând calculele, ajungem la valoarea frecvenţei de tăiere, 45.473 Hz. Întrucât formula de mai sus nu ia în considerare şi rezistenţa de sarcină din circuit, refacem graficul de mai sus, eliminând sarcina din circuit:
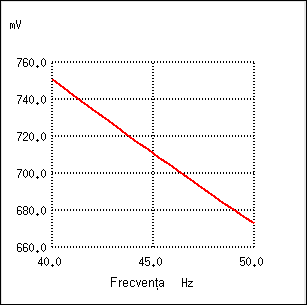
Este important de ţinut minte că răspunsul filtrului depinde de valorile componentelor acestuia precum şi de impedanţa sarcinii. Dacă ecuaţia frecvenţei de tăiere nu ia în considerare şi această impedanţă, sarcina nu este luată în considerare, iar valorile reale ale frecvenţei de tăiere vor fi diferite de valoarea calculată.
Folosirea filtrului trece-jos capacitiv pentru eliminarea zgomotului
O aplicaţie frecvenţă a filtrului trece-jos capacitiv este în cadrul circuitelor ce prezintă componente sau secţiuni susceptibile zgomotului electric. Un exemplu este suprapunerea zgomotului de curent alternativ peste liniile electrice de curent continuu folosite pentru alimentearea circuitelor sensibile prin capacitatea şi inductanţa mutuală parazită (Cp şi Mp:
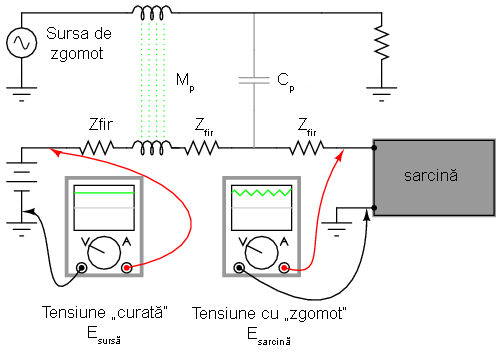
Aparatul de măsură din stânga măsoară o tensiune de alimentare în curent cotinuu „curată”. După realizarea cuplajului cu circuitul de curent alternativ, prin inductanţa mutuală şi capacitatea parazită, tensiunea măsurată la bornele sarcinii prezintă un amestec de curent continuu şi curent alternativ, componenta alternativă fiind cea nedorită. În mod normale ne-am aştepta ca Esarcină să fie identică cu Esursă datorită datorită faptului că nu există întreruperi ale conductorilor de la sursă la sarcină, iar cele două seturi de câte două puncte ar trebui să fie comune din punct de vedere electric. Totuşi, amplitudinea zgomotului poate varia în diferite puncte ale sistemului de curent continuu.
Scopul nostru este de a preveni asfel de zgomote în circuitul de curent continuu, iar pentru aceasta este suficientă conectarea unui filtru trece-jos la ieşirea circuitului, înainte de sarcină, pentru blocarea oricăror semnale de cuplaj nedorite. Sub forma cea mai simplă, acest filtru nu este nimic mai mult decât un condensator conectat direct la bornele sarcinii, acesta prezentând o impedanţă foarte mică faţă de orice zgomot de curent alternativ. Un asfel de condensator poartă numele de condensator de decuplare.
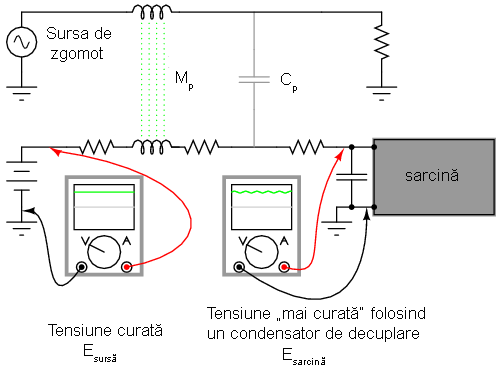
Capacitatea unui condensator de decuplare este în mod normal în jurul valorii de 0.1 µF, sau peste, fiind capacitatea minimă necesară pentru producerea unei impedanţe suficient de mari pentru scurt-circuitarea oricărui zgomot.
8.3 Filtrul trece-sus
Filtrul trece-sus este exact opusul filtrului trece-jos, după cum sugerează şi numele: permite trecerea semnalelor de frecvenţă înaltă şi blochează trecerea semnalelor de frecvenţă joasă. Modul de conectare al elementelor reactive în circuit este exact opus faţă de filtrele trece-jos.
Filtrul trece-sus capacitiv
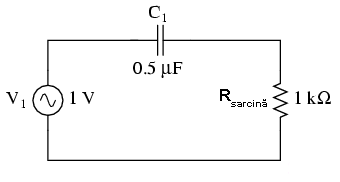
Impedanţa condensatorului din circuitul de mai sus creşte odată cu descreşterea frecvenţei. Această impedanţă în serie cu sarcina tinde să blocheaze semnalele de frecvenţă joasă ce ar putea ajunge pe sarcină.
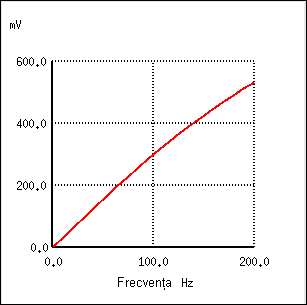
După cum se poate vedea în diagrama Bode, răspunsul filtrului capacitiv trece-sus creşte cu creşterea frecvenţei.
Filtrul trece-sus inductiv
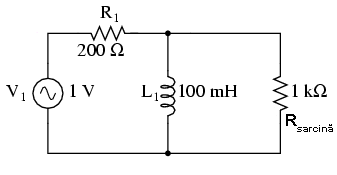
Impedanţa bobine scade odată cu scăderea frecvenţei. Aceasta impedanţă mică conectată în paralel cu sarcina, tinde să scurt-circuiteze semnalele de frecvenţă joasă, asfel că acestea nu mai ajung la sarcină. Prin urmare, mare parte a căderii de tensiune se va regăsi pe rezistorul R1.
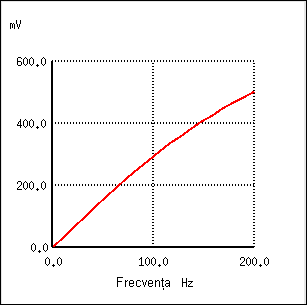
După cum se poate vedea în diagrama Bode, răspunsul filtrului inductiv trece-sus creşte cu creşterea frecvenţei.
Comparaţie între filtrele trece-sus inductive şi capacitive
De data aceasta, schema filtrului capacitiv trece-sus este mai simplă decât cea inductivă, necesitând doar un singur component în plus, un condensator. Din nou, puritatea reactivă a condensatoarelor faţă de bobine face ca filtrele capacitive să fie cel mai des folosite.
Frecvenţa de taiere
La fel ca în cazul filtrelor trece-jos, şi filtrele trece-sus au o frecvenţă de tăiere specifică. Peste valoarea aceste frecvenţă, tensiunea de ieşire este mai mare de 70.7% din valoarea tensiunii de intrare. Formula de calcul a frecvenţei de tăiere este aceeiaşi ca şi în cazul filtrelor trece-jos:
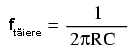
Rezistenţa din formulă, în cazul circuitului capacitiv trece-sus, este chiar rezistenţa de sarcină:
Filtrarea unui sistem audio
Să considerăm un sistem audio, ca şi exemplu. Un condensator conectat în serie cu tweeter-ul (înaltele) are rolul de filtru trece-sus, impunând circuitului de ieşire o impedanţă mare frecvenţelor joase (bas), prevenind asfel risipa de putere pe un difuzor ce este ineficient în reproducerea acestor sunete. Asemnănător, bobina conectată în serie cu woofer-ul (bas) are rolul de filtru trece-jos, permiţând doar trecerea acelor sunete pe care difuzorul le şi poate reproduce cu succes. În acest circuit simplu, difuzorul pentru frecvenţele medii este supus întregului spectru de frecvenţe produs de aparatul stereo. Câteodată se folosesc sisteme de filtrare mult mai elaborate, dar ideea generală este aceasta. În acest exemplu este prezentat doar un singur canal (stânga sau dreapta). Un sistem real ar conţine 6 difuzoare: 2 joase, 2 medii şi 2 înalte.
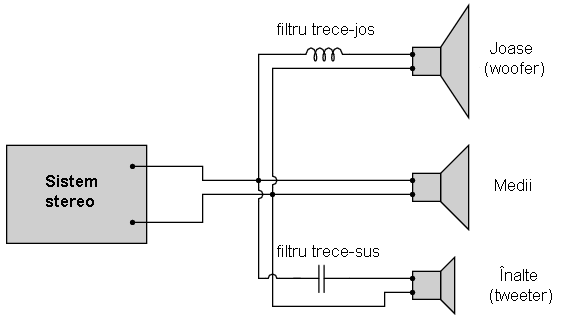
Pentru a mări şi mai mult performanţele acestui sistem, am putea construi un circuit de filtrare capabil să permită trecerea frecvenţelor ce se află între joase şi înalte spre difuzorul de medii, asfel încât să nu existe putere disipată (de frecvenţă înaltă sau joasă) pe un difuzor ce reproduce acest tip de sunete ineficient. Ceea ce vrem de fapt să realizăm, este un filtru trece bandă.
8.4 Filtrul trece-bandă
Există aplicaţii în care este nevoie de filtrarea unei anumite benzi de frecvenţe din totalul frecvenţelor prezente în semnal. Circuitele de filtrarea realizate pentru îndeplinirea acestui obiectiv pot dintr-un filtru trece-jos şi unul trece-sus, conectate împreună. Rezultatul este un filtru denumit trece-bandă. Diagrama prin care pot fi combinate cele două tipuri de filtre, arată în felul următor:
trece-jos şi trece-sus pentru formarea filtrului trece-bandă

Rezultatul acestei combinaţii serie dintre cele două filtre este un circuit ce va permite trecerea acelor frecvenţe ce se regăsesc între cele două limite, nici mai mari, nici mai mici.
Filtrul trece-bandă capacitiv
Folosind componente reale, circuitul electric al filtrului trece-bandă asfel conceput, arată asfel:
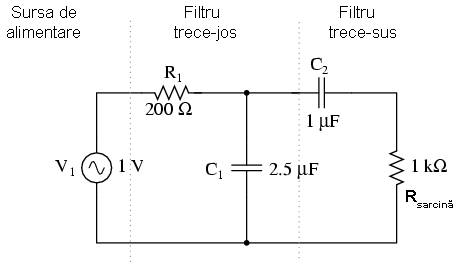
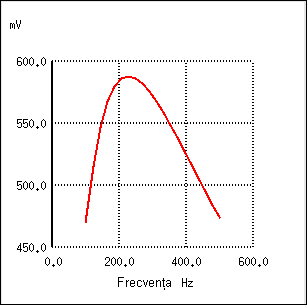
Să vedem şi răspunsul în frecvenţă (diagrama Bode) a filtrului capacitiv trece-bandă:
Filtrul trece-bandă inductiv
Filtrele trece-bandă pot fi construite folosind elemente inductive, dar, după cum am mai menţionat, filtrele capacitive sunt preferate în locul celor inductive datorită „purităţii” reactive a condensatoarelor. Circuitul electric al filtrului inductiv arată asfel:
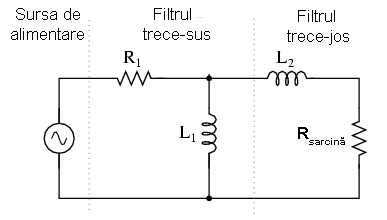
Faptul că filtrul trece-sus se află poziţionat înainte filtrului trece-jos, nu are nicio importanţă din punct de vedere al funcţionalităţii filtrului.
Limitele unui asfel de filtru
Deşi idea combinării celor două filtre, trece-jos şi trece-sus, într-unul singur, pentru a realiza un filtru trece-bandă, este bună, aceasta posedă şi unele dezavantaje. Deoarece acest tip de filtru funcţionează utlizând proprietatea fiecărui filtru în parte de a bloca frecvenţele nedorite, construirea unui asfel de filtru, asfel încât să nu blochează în anumită măsură şi frecvenţele din banda dorită, este de obicei dificilă. Atât filtrul trece-jos cât şi filtrul trece-sus vor bloca toate semnalele într-o anumită măsură, iar efectul lor combinat se traduce printr-o amplitudine redusă a semnalului chiar şi în domeniul frecvenţelor dorite (de trecere). Putem obseerva acest lucru din diagrama de mai sus, unde tensiunea sarcinii nu depăşeste valoarea de 0.6 V, deşi tensiunea sursei este de 1 V. Această atenuare a semnalului de ieşire devine şi mai pronunţată în cazul în care filtrul are un scop mult mai restrictiv (pantă mai mare a undei, banda de trecere a frecvenţelor mai îngustă).
8.5 Filtrul stop-bandă
Filtrul stop-bandă permite trecerea tuturor frecvenţelor ce se află peste sau sub un anumit domeniu/bandă de frecvenţe determinat de elementele sale coponente. Şi acest tip de filtru poate fi realizat prin conectarea unui filtru trece-jos cu un filtru trece-sus, doar că de data aceasta conectarea se realizează în paralel, nu în serie cum era cazul filtrului trece-bandă. Mai jos este prezentată diagrama bloc a filtrului:
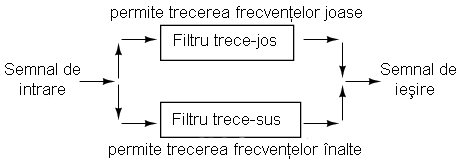
Filtrul stop-bandă capacitiv
Folosind componente reale, circuitul stop-bandă capacitiv arată în felul următor:
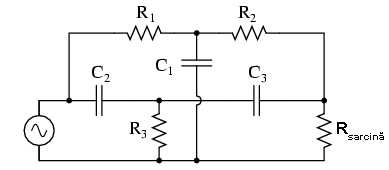
Filtrul trece-jos este compus din R1, R2 şi C1 în configuraţie „T”, iar filtrul trece-sus este compus din C2, C3 şi R3 de asemenea în configuraţie „T”. Împreună, cele două filtre formează filtrul stop-bandă cunoscut sub numele de „dublu T”; răspunsul acestui filtru este foarte precis atunci când sunt respectate următoarele proporţii în alegerea elementelor constituente:
R1 = R2 = 2(R3)
C2 = C3 = (0.5)C1
Utilizând aceste raţii, frecvenţa maximă de trecere poate fi calculată asfel:
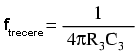
Putem vedea şi răspunsul în frecvenţă foarte bun al acestui filtru, folosind proprţiile de mai sus, în diagrama (Bode) de mai jos:
8.6 Filtre rezonante
Filtrele considerate până în acest moment au fost compuse exclusiv din condensatoare sau bobine, dar nu ambele tipuri de componente în acelaşi timp. Ştim că circuitele ce folosesc combinaţii de L şi C tind să rezoneze, iar această proprietate poate fi exploatată în construcţia filtrelor trece-bandă şi stop-bandă.
Circuitele LC serie prezintă o impedanţă minimă la rezonanţă, iar circuitele LC paralel impedanţă maximă la frecvenţa de rezonanţă. Există prin urmare două strategii de bază pentru construcţie filtrelor trece- respectiv stop-bandă.
Filtrul trece-bandă rezonant
Pentru acest tip de filtru, există două strategii: circuit LC serie sau LC paralel.
Filtrul trece-bandă în configuraţie LC serie
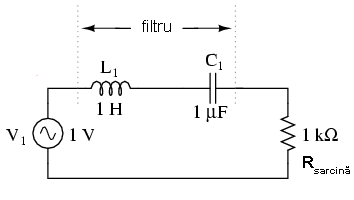
Circuitul LC serie permite trecerea semnalului la frecvenţa de rezonanţa (impedanţă mică - scurt-circuit), şi blochează toate celelalte frecvenţe (impedanţă mare - circuit deschis), asfel că acestea nu ajung la sarcină, după cum se poate vedea în diagramă.
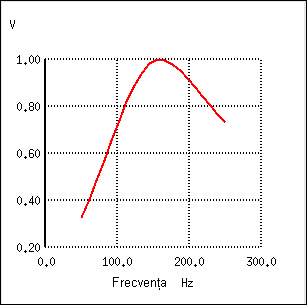
Putem observa că în cazul acestui tip de filtru, nu există practic nicio atenuare a semnalului în banda de trecere, asfel că tensiunea de ieşire pe rezistenţa de sarcină este aceeiaşi cu tensiunea de alimentare a sursei; acesta nu este şi cazul filtrelor construite exclusiv din condensatoare sau bobine. De asemenea, din moment ce principiul de funcţionare al filtrului se bazează pe principiul rezonanţei LC serie, frecvenţa de rezonanţă nefiind prin urmare afectată de valoarea rezistenţei prezentă în circuit, valoarea rezistenţei de sarcină nu va influenţa în niciun fel frecvenţa de trecere. Totuşi, diferite valori ale rezistenţei de sarcină vor duce la modificarea pantei diagramei Bode („selectivitatea” filtrului).
Filtrul trece-bandă în configuraţie LC paralel
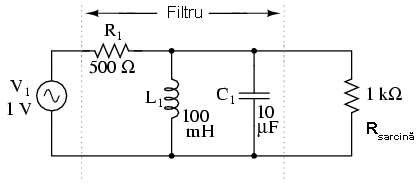
Circuitul LC paralel permite trecerea semnalului la frecvenţa de rezonanţa (impedanţă mare - circuit deschis) spre sarcină, şi blochează toate celelalte frecvenţe (impedanţă mică - scurt-sicircuit), căderea de tensiune regăsindu-se în marea ei parte pe R1, asfel că acestea nu ajung la sarcină, după cum se poate vedea în diagramă.
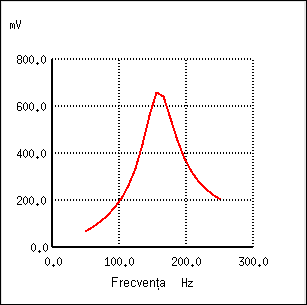
Acest tip de filtru rezonant, asemenea filtrelor trece-sus şi trece-jos, nu va putea transmite întreaga tensiune de la sursă spre sarcină datorită rezistorului conectat în serie ce va prelua tot timpul o parte din căderea de tensiune totală existentă în circuit.
Putem menţiona că acest tip de filtru trece-bandă rezonant este folosit pe scară largă în radiourile analogice, pentru selectarea unei anumite frecvenţe din cele recepţionate de antenă. Practic, se foloseşte un disc selector pentru alegerea postului de radio, disc ce modifică capacitatea unui condensator variabil dintr-un circuit LC paralel.
Filtrul stop-bandă rezonant
Din nou, avem două strategii la dispoziţie, circuitul LC serie sau LC paralel.
Filtrul stop-bandă rezonant în configuraţie LC serie
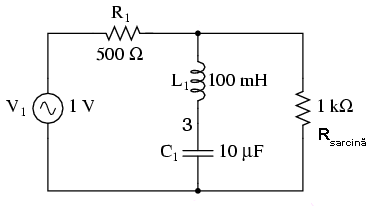
Folosit în această combinaţie, filtrul LC prezintă o impedanţă foarte scăzută faţă de semnal, la frecvenţa de rezonaţă, întreaga cădere de tensiune regăsindu-se pe rezistorul R1, iar semnalul nu este asfel „văzut” de sarcină.
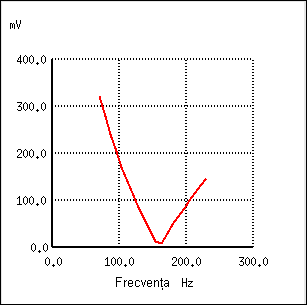
Filtrul stop-bandă rezonant în configuraţie LC paralel

Coponentele LC conectate în paralel prezintă o impedanţă mare la frecvenţa de rezonanţă, blocând asfel semnalele de la sursa spre sarcină, la frecvenţa respectivă, şi permite trecerea tuturor celorlalte semnale (alte frecvenţe decăt cea de rezonanţă) de la sursă spre sarcină.
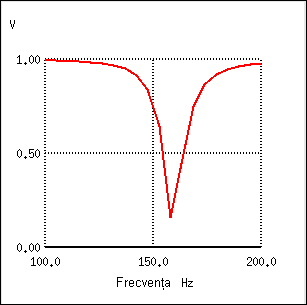
Din nou se poate observa faptul că absenţa unui rezistor serie duce la o atenuare minimă a semnalelor dorite. Amplitudinea semnalului la frecvenţa de trecere, pe de altă parte, este foarte mică. Cu alte cuvinte, acesta este un filtru foarte „selectiv”.
În toate aceste circuite de filtrare rezonante, selectivitatea depinde în mare măsură de „puritatea” bobinelor şi a condensatoarelor utilizate. În cazul în care există o rezistenţă parazită, aceasta va afecta abilitatea filtrului de discriminare precisă a frecvenţelor, şi este posibilă introducerea efectelor antirezonante ce afectează frecvenţele de trecere.
Filtre trece-jos şi trece-sus rezonante
După ce am analizat filtrele standard RC şi LC trece-jos şi trece-sus, ne-am putea imagina că se poate realiza o proiectare mai eficientă a acestor tipuri de filtre combinând efectele condensatoarelor şi a bobinelor în acelaşi circuit.
Filtru trece-jos capacitiv-inductiv
Bobinele ar trebui să blocheze trecerea frecvenţelor înalte, iar condensatorul ar trebui să blocheze şi el trecerea aceloraşi frecvenţe, efectele lor combinate permiţând doar trecerea semnalelor de frecvenţă joasă de la sursă spre sarcină.
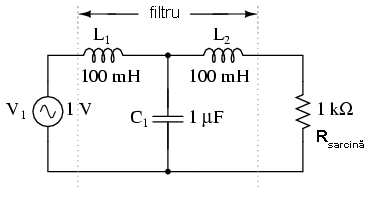
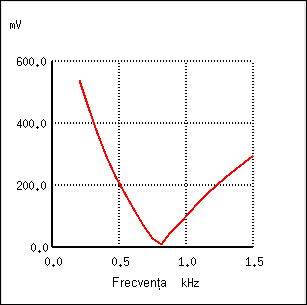
La prima vedere, aceasta pare o strategie bună, şi elimină rezistorul serie. Totuşi, trebuie realizat faptul că orice combinaţie condensator-bobină poate duce la efecte rezonante la o anumită frecvenţă, iar acesta nu este un lucru de dorit. Să urmărim răspunsul în frecvenţă a filtrului de mai sus, pe rezistenţa de sarcină (Rsarcină):
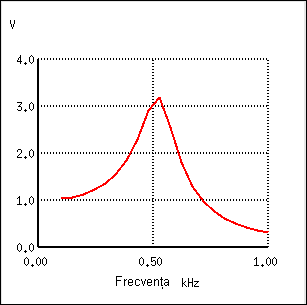
Ceea ce a fost gândit ca un filtru trece-jos s-a dovedit a fi un filtru trece bandă cu o frecvenţă de trecere în jurul valorii de 526 Hz, frecvenţa de rezonantă a condensatorului şi a bobinei în acest caz.
Problema este că impedanţa de intrare şi impedanţa de ieşire a filtrului LC trebuie să fie egală. Cu alte cuvinte, impedanţa sursei de alimentare trebuie să fie egală cu impedanţa de intrare a filtrului, iar impedanţa de ieşire a filtrului trebuie să fie egală cu impedanţa sarcinii (Rsarcină) pentru ca răspunsul filtrului să fie cel aşteptat. Impedanţa de intrare şi de ieşire a filtrului este radăcina pătrată a raportului dintre L şi C:
Z = (L/C)1/2)
Folosind valorile componentelor de pe circuit, putem afla impedanţa filtrului şi impedanţele sursei şi a sarcinii necesare.
Pentru L = 100 mH, C= 1µF
Z = (L/C)1/2=((100 mH)/(1 µF))1/2 = 316 Ω
Asfel, în circuitul de mai sus putem adăuga rezistorul Rg de 316 Ω în serie cu sursa de tensiune şi modificăm Rsarcină de la 1.000 Ω la 316 Ω. Dacă ar fi fost necesară alimentarea unei sarcini de 1.000 Ω, am fi putut modifica raportul L/C pentru a păstra egalitatea faţă de sarcină.
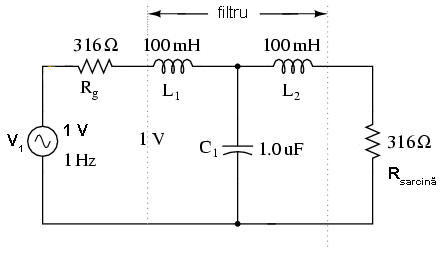
Răspunsul în frecvenţă al filtrului arată de data aceasta mult mai bine: