< Curent alternativ

7 Frecvente combinate

7.1 Introducere

Circuitele studiate până în acest moment au fost alimentate integral într-o singură frecvenţă sinusoidală. În multe aplicaţii însă, frecvenţa unică este mai degraba excepţia decât regula. De multe ori întâlnim circuite unde frecvenţa tensiunii de alimentare este compusă din mai multe frecvenţe individuale luate împreună. Pe lângă asta, formele de undă ale tensiunii pot avea şi alte forme, nu doar sinusoidale, caz în care ele intră in categoria formelor de undă ne-sinusoidale.

Întâlnim de asemenea cazuri în care semnalul de curent continuu este combinat cu cel de curent alternativ: forma de undă este suprapusă peste un semnal de curent continuu. Rezultatul unei asfel de combinaţii este un semnal variabil în intensitate (amplitudine) dar nu şi în polaritate, sau polaritatea sa variază asimetric. Indiferent de caz, atunci când avem mai multe frecvenţe în acelaşi circuit, analiza acestuia este mult mai complexă decât ceea ce am văzut până acum.

Cuplajele inductive şi capacitive accidentale

Unele situaţii de semnale de curent sau tensiune cu frecvenţe multiple sunt create accidental, fiind rezultatul conexiunilor accidentale dintre circuite, denumite cuplaje, cauzate de capacităţile sau inductanţele parazite dintre conductorii acelor circuite. Un exemplu clasic de cuplaj este întâlnit des în industrie, unde o reţea de curent continuu este plasată în apropierea unei reţele de curent alternativ. Prezenţă tensiunilor înalte şi a curenţilor alternativi pot duce la modificarea comportamentului reţelei de curent cotinuu. Capacitatea parazită formată între izolaţiile celor două reţele poate induce tensiune (faţă de împământare) de la cea de curent alternativ la cea de curent continuu, iar inductanţele parazite formate între cele două lungimi ale conductorilor pot duce la situaţia în care curenţii primei reţele să inducă tensiune pe cale electromagnetică în conductorii celei de a doua reţele. Rezultatul este o combinaţie de semnale de curent continuu şi alternativ. Următoarea schemă prezintă modul în care sursa de zgomot de curent alternativ se poate cupla la circuitul de curent alternativ prin inductanţa (M_p) şi capacitatea parazită (C_p):

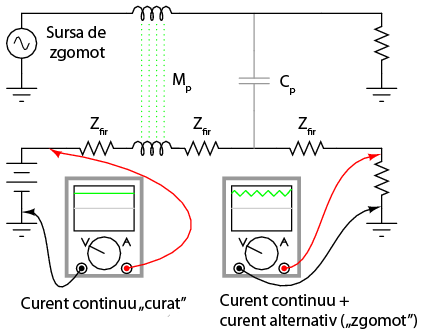
Folosirea cablurilor răsucite şi ecranate

Atunci când tensiunile alternative parazite se mixează cu semnalele de curent continuu, rezultatele sunt de obicei nedorite. Din acest motiv, reţeaua de alimentare cu energie electrică (curent alternativ, puteri mari) trebuie să fie neapărat separată de reţelele de semnal (curent continuu, puteri mici), iar semnalele transmise prin intermediul cablurilor răsucite (twisted) formate din doi conductori, şi nu doar printr-un singur fir şi conexiunea acestuia la împământare:

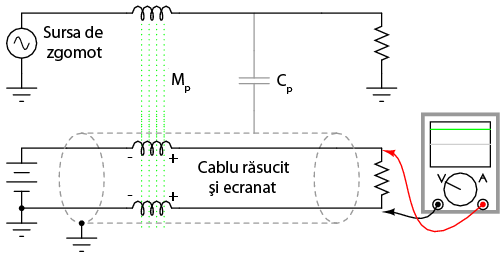
Ecranajul cablului - o folie metalică înfăşurată în jurul celor doi conductori izolaţi - este conectat la împământare, şi izolează ambii conductori faţă de cuplajul electrostatic (capacitiv), blocând orice câmp electric exterior. Răsucirea celor doi conductori, unul lângă celălalt, anulează orice cuplaj electromagnetic (inductanţă mutuală), întrucât orice tensiune parazită indusă va fi aproximativ egală în amplitudine dar defazată cu 180^o (opoziţie de fază) în ambii conductori, cele două semnale anulându-se practic între ele, rezultând o diferenţă de potenţial aproape nulă.

Cuplajul poate să apară şi între două seturi de conductori de curent alternativ, caz în care ambele semnale vor purta o combinaţie de frecvenţe:

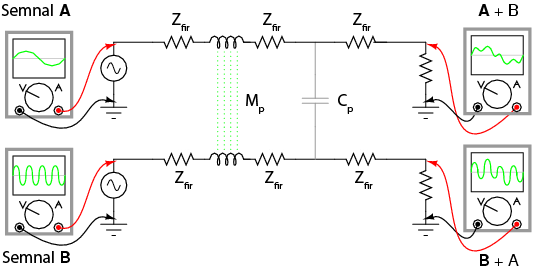
Alte moduri de generare a frecvenţelor multiple

Cuplajul este doar unul dintre exemplele de combinare a frecvenţelor, fiind accidental şi de nedorit. În alte cazuri însă, semnalele cu frecvenţe multiple sunt rezultatul proiectării voite a circuitului sau reprezintă o calitate intrinsecă a semnalului analizat. Cel mai uşor mod de producere a semnalelor cu frecvenţe multipe este conectarea surselor de tensiune de frecvenţe diferite în serie:

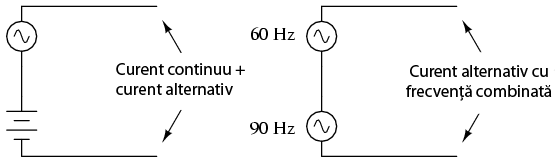
În unele cazuri, frecvenţa mixată a semnalului este produsă de o singură sursă de tensiune. Un exemplu este microfonul, un traductor ce transformă presiunea aerului datorată frecvenţelor audio într-o tensiune a cărei formă de undă corespunde acestor frecvenţe ne-sinusoidale. Foarte puţine sunete naturale sunt formate dintr-o vibraţie sinusoidală pură, ci, majoritatea sunt compuse dintr-o serie de vibraţii la frecvenţe şi amplitudini diferite combinate într-un singur semnal final.

Sunetele muzicale

Acordurile muzicale sunt produse printr-un amestec de frecvenţe cu frecvenţă de bază, fiecare dintre acestea fiind un multiplu al frecvenţei fundamentale. Chiar şi o simplă notă de pian este compusă dintr-o frecvenţă predominantă amestecată cu alte frecvenţe (armonici, fiecare dintre acestea fiind un multiplu al primei (fundamentala). Pentru ilustrare, putem considera următorul tabel, în care frecvenţa fundamentală este de 1.000 Hz (cifră luată la întâmplare):

Frecvenţa (Hz)	Termen
1000	armonica 1, sau fundamentala
2000	armonica a 2-a
3000	armonica a 3-a
4000	armonica a 4-a
5000	armonica a 5-a
6000	armonica a 6-a
7000	armonica a 7-a

Unele instrumente muzicale nu pot produce anumite tipuri de frecvenţe armonice. De exemplu, un „instrument” realizat dintr-un tub deschis la un capăţ şi închis la celălalt (precum o sticlă) nu va putea produce armonice pare. Un asfel de instrument, construit asfel încât să producă o frecvenţă fundamentală de 1.000 Hz, va produce şi armonici de 3.000, 5.000, 7.000, etc. Hz, dar nu va putea produce 2.000, 4.000, 6.000, etc. Hz.

O formă de undă pur sinusoidală (frecvenţă unică, „curată”), neavând nicio armonică, sună „sec” urechii umane. Majoritatea instrumentelor muzicale nu sunt capabile să producă sunete atât de „simple”.

7.2 Forme de undă dreptunghiulare

Este cunoscut faptul că orice semnal periodic (ce se repetă în timp) ne-sinusoidal poate fi reprezentat ca şi combinaţie de semnale continue, sinusoidale şi/sau cosinusoidale (semnal sinusoidal defazat cu 90 de grade) de frecvenţe şi amplitudini variate. Acest lucru este perfect valabil indiferent cât de „ciudat” sau „contorsionat” ar părea semnalul analizat. Atâta timp cât este periodic, se poate reduce la tipul de combinaţii prezentate mai sus. Într-un caz particular, formele de undă dreptunghiulare sunt echivalente din punct de vedere matematic cu suma unui semnal sinusoidal fundamental, de o anumită frecvenţă, plus o serie infinită de multiplii impari ai frecvenţei fundamentale cu amplitudini descrescătoare.

Acest adevăr, perfect demonstrabil, al formelor de undă pare greu de crezut. Totuşi, dacă o formă de undă dreptunghiulară este de fapt o serie infinită de armonici sinusoidal adunate împreună, ar trebui să putem demonstra acest lucru însumând câteva armonici sinusoidale şi obţinuând o aproximare a semnalului dreptunghiular. Vom încerca să facem acest lucru în continuare.

Circuitul considerat constă în cinci surse de tensiune, de amplitidini şi frecvenţe diferite, conectate în serie. Armonicele considerate sunt: cea fundamentală (prima) la o frecvenţă de 50 Hz, armonica a 3-a (3*50 = 150 Hz), a 5-a, a 7-a şi a 9-a (9*50 = 450 Hz). Amplitudinile semnalelor nu sunt nici ele aleatoare, ci, constau din fracţia 4/π înmulţită cu fracţiile 1 (4/π*1 = 4/π V), 1/3, 1/5, 1/7 şi 1/9 (4/π*1/9 =4/9π V) , în funţie de armonica corespunzătoare.

Primul grafic reprezintă tocmai frecvenţa fundamentală, la 50 Hz şi amplitudine de 4/π, adică aproximativ 1.27 V:

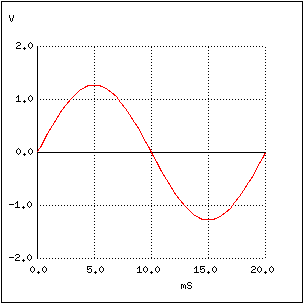
În următorul grafic, vom vedea ce se întâmplă cu acest semnal sinusoidal pur atunci când îl combinăm cu armonica a 3-a (150 Hz). Din acest moment, nu mai seamană cu un semnal sinusoidal pur (semnalul combinat este cel cu roşu):

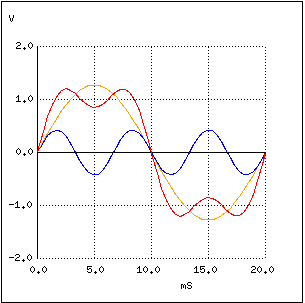
Panta formei de undă la intersecţia cu axa orizontală a timpului este mult mai mare acum, semn că forma de undă iniţială se apropie de cea dreptunghiulară. Să adăugăm în continuare şi armonica a 5-a pe grafic:

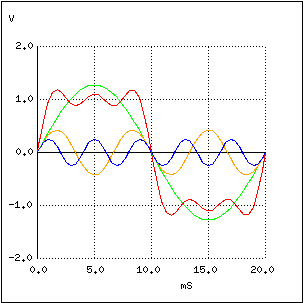
Armonica a 5-a (250 Hz) este reprezentată pe graficul de mai sus cu albastru, iar efectele combinate a celor două armonici cu fundamentale sunt reprezentate cu roşu.

Putem observa cum vârful formei de undă s-a aplatizat faţă de situaţia iniţială, iar panta a crescut şi mai mult faţă de cazul precedent. Adăugăm pe rând şi armonicele a 7-a, respectiv a 9-a:

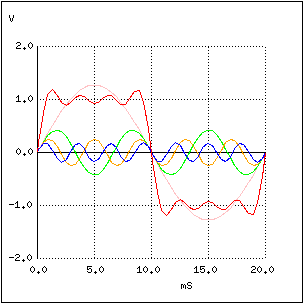
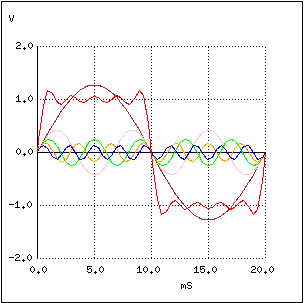
Rezultatul însumării celor 5 armonici, cu amplitidinile de rigoare, reprezintă o aproximare destul de bună a unui semnal dreptunghiular. Scopul acestui exemplu a fost ilustrarea modului de construire a unui semnal dreptunghiular folosind semnale sinusoidale multiple la frecvenţe diferite pentru a demonstra faptul că un semnal pur dreptunghiular este într-adevăr echivalent cu o serie de semnale sinusoidale. Atunci când aplică un semnal dreptunghular într-un circuit ce conţine elemente reactive (condensatoare şi/sau bobine), acele componente se comportă ca şi cum am fi aplicat mai multe tensiune de frecvenţe diferite în acelaşi timp, ceea ce de fapt am şi făcut.

Faptul că semnalele ne-sinusoidale perioadice sunt echivalente cu o serie de semnale de curent cotinuu, sinusoidale şi/sau cosinusoidale este o consecinţă intrinsecă a modului de „funcţionare” al semnalelor: o proprietate fundamentală a tuturor formelor de undă, indiferent că sunt electrice sau mecanice. Procesul matematic de reducere a acestor forme de undă ne-sinusoildale ca sumă a componentelor sale la frecvenţe şi amplitudini diferite, poartă numele de analiză Fourier, fiind un proces destul de complicat. Analziza Fourier este în schimb uşor de făcut folosind un calculator şi un algoritm numit transformata Fourier, ceea ce vom încerca să facem în continuare.

Să luăm din nou exemplul semnalului dreptunghiular, simetric, cu amplitudinea de 1 V:

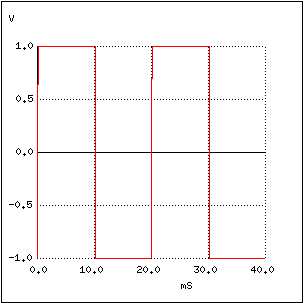
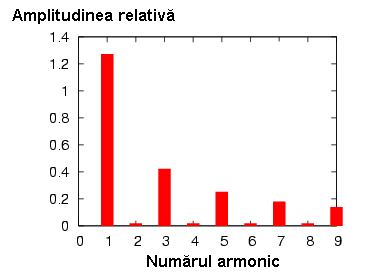
În graficul de mai sus, formele de undă sunt împărţite în funcţie de frecvenţele lor sinusoidale, până la armonica a 9-a. Amplitudinile armonicilor pare sunt aproximativ zero, iar a celor impare descresc de la 1 la 9 (prima este cea mai mare, ultima cea mai mică).

Un dispozitiv construit special pentru afişarea - nu şi controlul - amplitudinii fiecărei frecvenţe a unui semnal format din mai multe frecvenţe, se numeşte analizor spectral, iar procesul de analiză a unui semnal în acest mod, poartă numele de analiză spectrală

Deşi poate părea ciudat, orice formă de undă periodică ne-sinusoidală este de fapt echivalentă cu suma unei serii de unde sinusoidale de frecvenţe şi amplitudini diferite. Formele dreptunghiulare sunt doar un singur caz, dar nu unicul.

7.3 Analiza spectrală

Analiza Fourier computerizată, în special sub forma algoritmului FFT (Fast Fourier Transform), este un instrument excelent pentru înţelegerea formelor de undă şi a componentelor spectrale ale acestora.

Pentru început, luăm o formă de undă sinusoidală (aproape perfectă) la frecvenţa de 523.25 Hz, semnal produs cu ajutorul unei claviaturi electronice. Graficul formei de undă este de mai jos este luat de pe afişajul unui osciloscop şi prezintă amplitudinea tensiunii (axa verticală) cu timpul (axa orizontală):

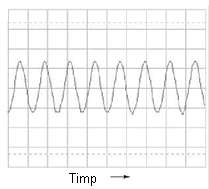
Dacă observăm cu atenţie unde sinusoidală putem vedea că există anumite imperfecţii ale formei acestia. Din păcate, acesta este rezultatul echipamentului folosit pentru analiza undei. Asfel de caracteristici datorate echipamentelor de testare sunt cunoscute sub denumirea tehnică de artefacte: fenomene a cărei existenţă se datorează aparatelor de măsură folosite pentru derularea experimentului.

Dacă urmărim această tensiune alternativă pe un analizor spectral, rezultatul este puţin diferit, dar semnalul analizat este exact acelaşi:

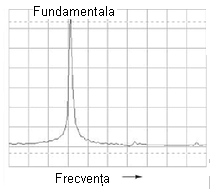
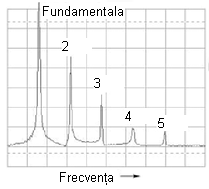
După cum se poate vedea, orizontala este marcată şi reprezintă „Frecvenţa”, adică domeniul măsurătorii. Vârful curbei reprezintă frecvenţa dominantă, considerată mai sus (523.25 Hz), iar înălţimea acestuia este amplitudinea semnalului pentrua această frecvenţă.

Dacă vom combina mai multe note muzicale pe aceeiaşi claviatură electronică şi măsurăm rezultatul, din nou cu un osciloscop, putem vedea foarte uşor faptul că semnalul creşte în complexitate. Semnalul final este de fapt o combinaţie de semnale sinusoidale de frecvenţe şi amplitudini diferite:

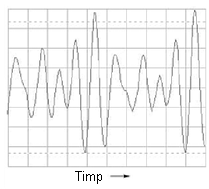
Analiza spectrală este mult mai uşor de analizat, întrucât fiecărei note (sinusoidale) îi corespune pe grafic un vârf, în funcţie de frecvenţa sa:

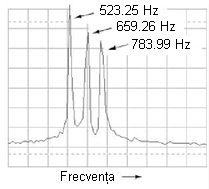
Să luăm în continuare alte forme de undă muzicale, şi să le analizăm grafic:

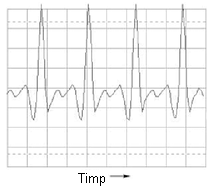
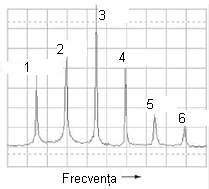
Primul vârf îl reprezintă fundamentala, iar celelalte vârfuri (2-6) sunt armonicele formei de undă ne-sinusoidale considerate mai sus.

Un alt exemplu:

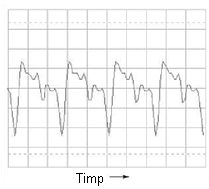
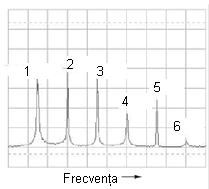
Să luăm din nou o formă de undă dreptunghiulară:

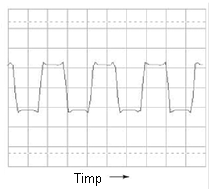
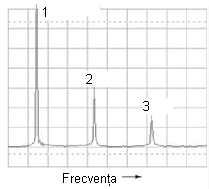
Conform analizei spectrale, această formă de undă nu conţine armonici pare, doar impare. Cu toate că afişajul osciloscopului nu permite vizualizarea frecvenţelor peste armonica a 6-a, armonicile impare continuă la infinit, cu o amplitudine din ce în ce mai mică.

Să considerăm şi un semnal triunghiular:

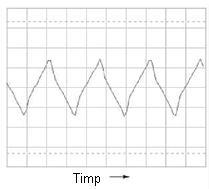
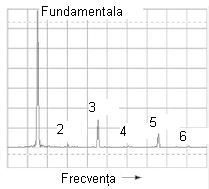
În acest caz, nu există practic armonici pare: singurele armonici sunt cele pare. Deşi putem vedea vârfuri mici pentru armonicele 2, 4 şi 6, acestea se datorează imperfecţiunilor formei de undă triunghiulare. O formă de undă triunghiulară perfectă, nu produce armonici pare, la fel ca în cazul formei de undă dreptunghiulare. Este evident însă că cele spectrul celor două nu este identic: amplitudinile armonicelor respective nu sunt identice.

Să analizăm şi semnalul dinte de fierăstrău:

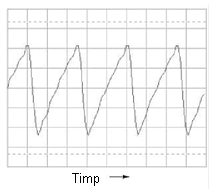
Diferenţa dintre armonicile pare şi impare

Distincţia dintre o formă de undă ce conţine armonici pare şi o formă de undă ce nu conţine aceste armonici se poate observa grafic, înaintea realizării analizei spectrale. Diferenţa constă în simetria faţă de axa orizontală a undei. O formă de undă simetrică faţă de axa orizontală nu va prezenta armonici pare:

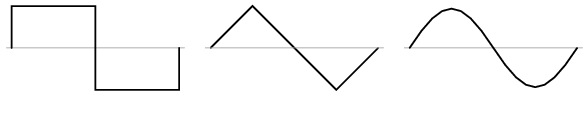
Formele de undă de mai sus, fiind toate simetrice faţă de orizontală, conţin doar armonici impare (forma de undă pur sinusoidală conţine doar armonica de gradul întâi, fundamentala).

Cele care nu sunt simetrice faţă de orzontală, conţin însă şi armonici pare:

Trebuie înţeles faptul că simetria se referă exclusiv la axa orizontală a undei, şi nu neapărat la axa orizontală a timpului. Să luăm de exemplu aceleaşi forme de undă, dar însumate cu o componentă de curent continuu, asfel încât graficul lor este deplasat în sus, sau în jos, faţă de axa timpului (în cazul precedent, componenta de curent continuu era zero, asfel încât cele două axe orizontale conincideau). Analiza armonică a acestor forme de undă nu va fi diferită faţă de cele de mai sus, singura diferenţă fiind componenta de curent continuu, care însă nu afectează în niciun fel conţinutul armonicilor (frecvenţa ei este zero):

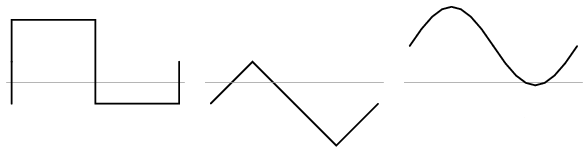
Acelaşi lucru este valabil şi pentru formele de undă nesimetrice faţă de orizontală, conţinutul armonic al acestor forme de undă nu va fi afectat de introducerea componentei de curent continuu:

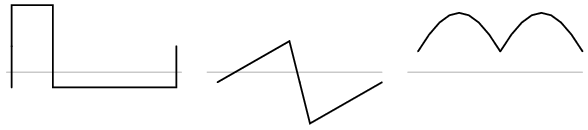
7.4 Efecte asupra circuitelor

Principiul conform căruia formele de undă periodice ne-sinusoidale sunt compuse dintr-o serie de unde sinusoidale de frecvenţe şi amplitudini diferite, este o proprietate generală a formelor de undă şi are o importanţă practică în studiul circuitelor de curent alternativ. Acest lucru înseamnă că de fiecare dată când întâlnim o formă de undă ne-sinusoidală, comportamentul circuitului va fi acelaşi ca şi în cazul în care am introduce deodată, în circuit, tensiuni de frecvenţe diferite.

Când un circuit de curent alternativ este alimentat de la o sursă de tensiune ce conţine o combinaţie de forme de undă de frecvenţe diferite, componentele acelui circuit vor răspunde diferit fiecărei frecvenţe în parte. Orice component reactiv din circuit, precum condensatorul şi bobina, va avea simultan o impedanţa unică şi diferită faţă de fiecare frecvenţă prezentă în circuit. Din fericire, analiza unui asfel de circuit este destul de uşor de realizat apelând la teorema superpoziţiei, considerând sursa de alimentare cu frecvenţe multiple ca un set de surse cu frecvenţe unice conectate în serie; analiza circuitului se face considerând fiecare „sursă” în pare, însumând la final rezultatele pentru a determina efectul total asupra circuitului:

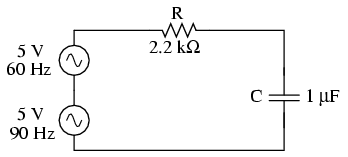
Primul pas constă în analiza circuitului alimentat doar cu sursa de tensiune de 60 Hz:

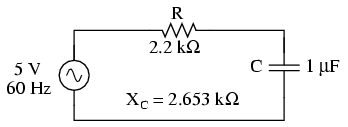
Apoi analizăm circuitul considerând doar efectele sursei de tensiune de 90 Hz:

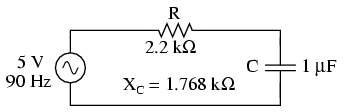
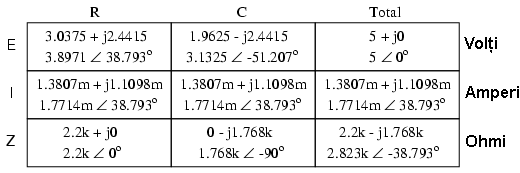
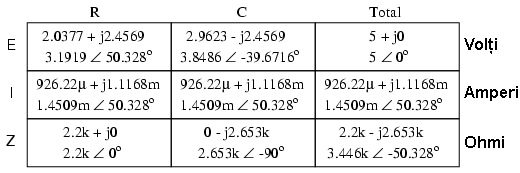
Folosind teorema superpoziţiei (suma efectelor celor două surse de tensiune) pentru căderile de tensiune pe rezistor (R) şi condensator (C), obţinem:

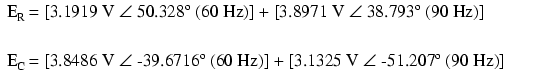
Pentru că cele două tensiuni se află la frecvenţe diferite, nu putem obţine un rezultat final cu o singură valoare a tensiunii, precum putem aduna două tensiuni de amplitudini şi faze diferite dar de aceeiaşi frecvenţă. Cu ajutorul numerelor complexe, putem reprezenta amplitudinea şi faza formelor de undă, dar nu şi frecvenţa.

Ceea ce putem concluziona după aplicarea teoremei superpoziţiei, este că, pe condensator, căderea de tensiune va fi mai mare pentru componenta de 60 Hz faţă de componenta de 90 Hz. În cazul bobinei, este exact invers. Acest lucru este important de realizat, având în vedere faptul că tensiunile celor două surse de alimentare sunt, de fapt, egale. Este important de luat în considerare acest răspuns nesimetric al componentelor circuitului (cap. următor?!). p>