< Curent alternativ
13 Linii electrice lungi
13.1 Circuitele electrice şi viteza luminii
Să presupunem că avem un circuit electric simplu, format dintr-o baterie, o lampă şi un întrerupător. La închiderea întrerupătorului, lampa se aprinde instant. La deschiderea întrerupătorului, lampe se stinge instant.

De fapt, aprinderea lămpii durează o mică fracţiune de secundă până se încălzeşte şi emite lumină, timp necesar pentru ca valoarea curentului să devină suficient de mare. Prin urmare, efectul nu este instantaneu. Pentru aplicaţiile practice însă, putem considera că efectul este imediat, atunci când lampa şi întrerupătorul se află în vecinătate, întrucât „deplasarea” electronilor în conductori are loc cu o viteză foarte mare, şi anume, viteza luminii (aproximativ 300.000 de kilometri pe secundă). Ce s-ar întâmpla însă dacă conductorii electrici ai unui circuit ar avea o lungime de 300.000 de kilometri? Din moment ce ştim că efectele electricităţii a o viteză finită (deşi foarte mare), un set de conductori foarte lungi ar introduce o întârziere de timp în circuit, asfel că acţionarea întrerupătorului şi aprinderea/stingerea lămpii nu ar mai fi instantanee:
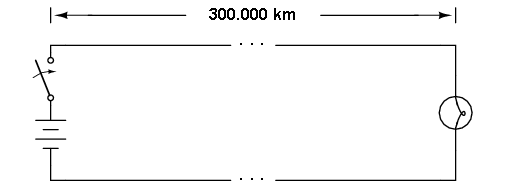
Presupunând că filamentul lămpii nu necesită încălzire, iar rezistenţa în lungul celor 600.000 de km de fire (dus-întors) este zero, lampa se va aprinde în aproximativ o secundă de la închiderea întrerupătorului. La închiderea întrerupătorului, lampa va continua să primească putere pentru încă o secundă, apoi se va stinge.
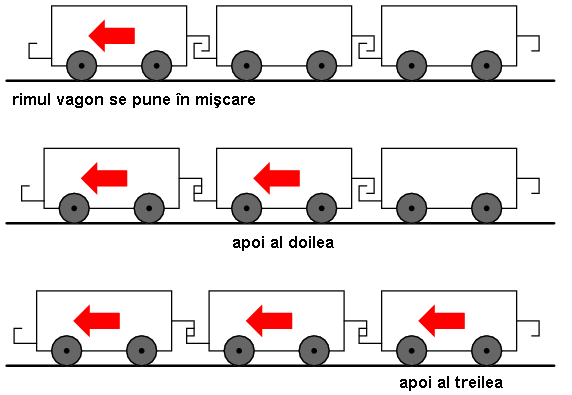
Ne putem imagina comportamentul electronilor printr-un conductor ca fiind echivalent cu vagoanele unui tren, legate între ele, dar prezentând o anumită „cursă” (distanţa parcusă de un vagon faţă de celălat, asfel încăt elementele de legătură să fie perfect întinse; doar după parcurgerea acestei distanţă, vagonul al doilea poate fi tras de primul vagon). Asfel, când trenul se pune în mişcare, nu toate vagoanele vor porni deodată, ci locomotiva trage primul vagon, după eliberarea cursei, primul vagon trage al doilea vagon după eliberarea cursei, etc. Asfel, mişcarea este transferată de la vagon la vagon la viteza maximă permisă de cursă, dar la o viteză mult mai mare decât viteza individuală a vagoanelor:
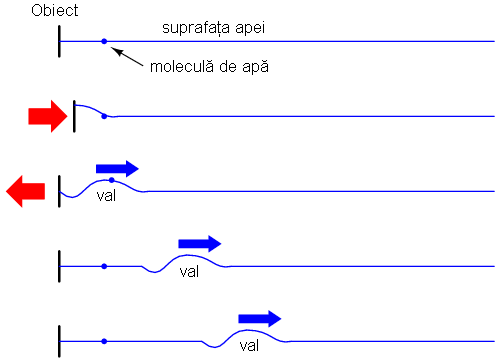
O altă analogie estea cea a valurilor în apă. Să presupunem că punem în mişcare un obiect plan pe suprafaţa apei, asfel încât acesta produce o serie de valuri în urma sa. Apa se va „deplasa” datorită faptului că moleculele sale se ciocnesc una de cealaltă, transferând energia de mişcare de-a lungul suprafeţei apei cu o viteza mai mare decât viteza individuală a moleculelor:
În aceeiaşi ordine de idei, „unda de curent” se deplasează cu viteza luminii, deşi electronii individuali nu au o viteză într-atât de mare. Într-un circuit foarte lung, această diferenţă de viteză, această „cuplare” a electronilor (exemplul trenului), devine vizibilă sub forma unei întârzieri între acţiunea întrerupătorului şi efectul asupra lămpii.
13.2 Impedanţa caracteristică
Să presupunem totuşi, că am avea un set de conductori de lungime infinită, fără nicio lampă conectată la capăt. Ce s-ar întâmpla la închiderea întrerupătorului. Din moment ce nu avem nicio sarcină conectată la bornele sale, acest circuit este de fapt deschis. Nu va exista deloc curent prin acest circuit?
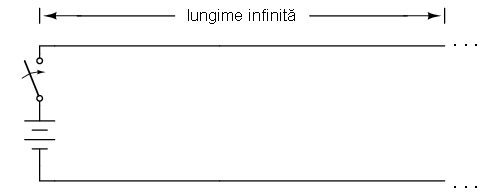
Chiar dacă am putea elimina rezistenţa firelor prin folosirea superconductoarelor în acest „experiment”, nu am putea elimina însă capacitatea formată în lungimile conductorilor. Orice pereche de conductori separaţi între ei printr-un mediu izolant, prezintă o anumită capacitate electrică parazită între ei.
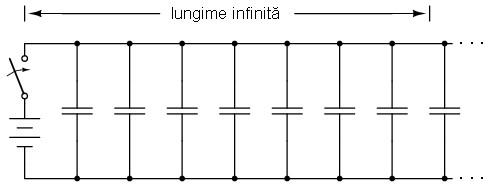
Aplicarea unei diferenţe de potenţial între doi conductori, duce la formarea unui câmp electric între acei doi conductori. Acest câmp electric va stoca energie, iar aceasta va duce la o opoziţie faţă de variaţia tensiunii, efect descris de ecuaţia i = C(de/dt), şi anume, curentul va fi proporţional cu rata de variaţia a tensiunii cu timpul. Asfel, la închiderea întrerupătorului, capacitatea dintre cei doi conductori va reacţiona împotriva creşterii bruşte (variaţie) a tensiunii, ceea ce va duce la apariţie unui curent prin circuit (de la sursă). Conform ecuaţiei, o variaţie instantă a tensiunii aplicate (produsă de închiderea perfectă a întrerupătorului) ar da naştere unui curent de încărcare infinit.
Cu toate acestea, curentul prin cei doi conductori paralelil nu va fi infinit, deoarece există o anumită impedanţă serie în lungul conductorilor, datorită inductanţei acestora. Apariţia unui curent, prin orice conductor, dă naştere unui câmp magnetic proporţional cu valoarea acestuia. Acest câmp magnetic va stoca energie, iar acest fapt va duce la o opoziţie faţă de variaţia curentului. Fiecare conductor va prezenta un câmp magnetic datorat trecerii curentului, iar căderea de tensiune ce ia naştere se calculează cu ecuaţia e = L(di/dt). Această cădere de tensiune limitează rata de variaţie a tensiunii în lungul capacitătilor distribuite, prevenind creşterea curentului spre infinit.
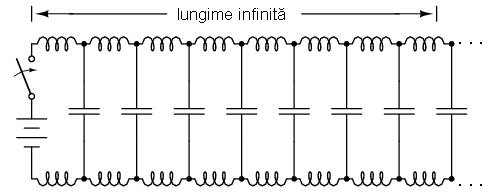
baterie şi întrerupător şi conductori de lungime infinită; închiderea
întrerupătorului şi apariţia câpurilor electrice şi magnetice
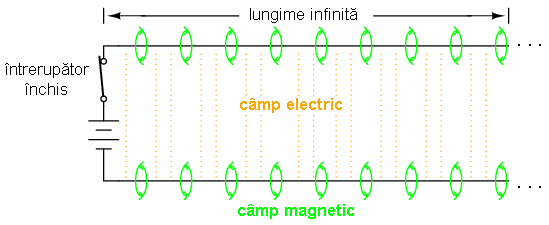
Deoarece transferul de mişcare al electronilor celor doi conductori de la unul la celălalt se realizează la viteza luminii, „frontul de undă” al variaţiei tensiunii şi curentului se va propaga în lungimea conductorilor cu aproximativ aceeiaşi viteză, ducând la încărcarea progresivă la valoarea maximă de tensiune şi curent a capacităţilor şi inductanţelor distribuite, asfel:
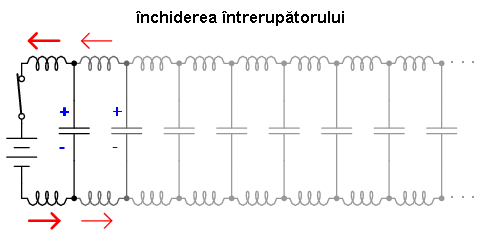
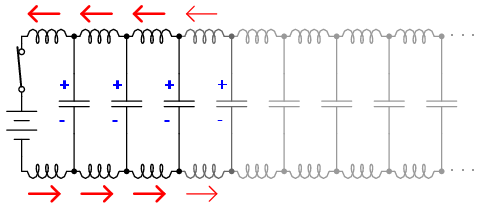
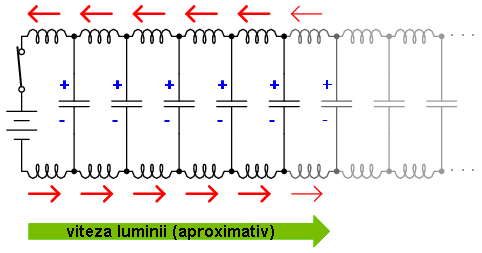
Rezultatul final al acestor interacţiuni este un curent constant, de amplitudine limitată, prin sursa de tensiune (baterie). Din moment ce lungimea conductoarelor este infinită, capacităţile lor distribuite nu se vor putea încărca niciodată la tensiunea sursei, iar inductanţele distribuite nu vor permite niciodată un curent de încărcare nelimitat. Cu alte cuvinte, această pereche de conductori va „trage” curent de la sursă atâta timp cât întrerupătorul este închis, comportându-se precum o sarcină constantă. În acest caz, firele electrice nu mai sunt simple conductoare de curent electric, ci constituie ele însele un component al circuitului, cu caracteristici unice care trebuiesc luate în considerare. Spunem în acest caz, că cele două perechi de conductoare sunt linii de transmisie.
Pentru o sarcină constantă, răspunsul liniilor de transmisie, la aplicarea unei tensiuni, este rezistiv şi nu reactiv, deşi sunt compuse în mare parte din inductanţe şi capacităţi (presupunând rezistenţa conductorilor ca fiind zero). Merită menţionat acest lucru, deoarece, din punctul de vedere al bateriei, nu există nicio diferenţă între un rezistor ce disipă tot timpul energie şi un set de linii electrice infinite ce abosrbă energie tot timpul. Impedanţă (rezistenţa) acestei linii, măsurată în Ohmi, poartă numele de impedanţă caracteristică, şi este o cantitate ce depinde exclusiv de geometria celor doi conductori. Pentru un set de conductori paraleli, cu aer pe post de dielectric, impedanţa caracteristică poate fi calculată asfel:
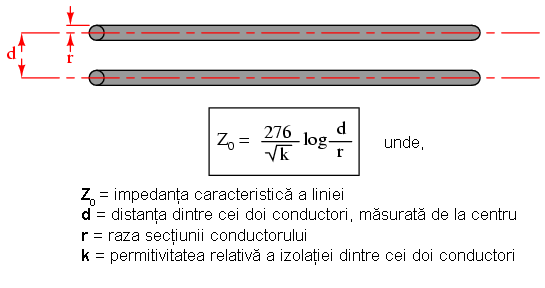
Dacă linia de transmisie este un cablu coaxial, impedanţa caracteristică se calculează asfel:
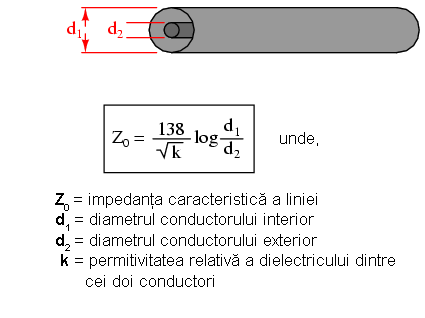
În ambele ecuaţii se folosesc aceleaşi unităţi de măsură. Dacă dielectricul dintre cei doi conductori nu este aer (sau vid), atât impedanţa caracteristică cât şi viteza de propagare a undelor vor avea de suferit. Raportul dintre viteza reală de propagare a undelor într-o linie de transmisie şi viteza luminii, poartă numele de factorului de viteză al acelei linii.
Factorul de viteză depinde doar de permitivitatea relativă a materialului izolator (dielectric), cunoscută şi sub numele de constanta dielectrică, şi definita ca raportul dintre permitivitatea electrică a materialului respectiv şi permitivitatea electrică a vidului. Factorul de viteză a oricărui tip de cablu (coaxial sau alt tip), poate fi calculat cu următoarea formulă:

Impedanţa caracteristică mai este cunoscută şi sub numele de impedanţă naturală, şi se referă la rezistenţa echivalentă a liniei de transmisie dacă lungimea acesteia ar fi infinită, datorită capacităţilor şi inductanţelor distribuite.
Se poate vedea din ecuaţiile de mai sus, că impedanţa caracteristică (Z0) a liniilor de transmisie creşte odată cu creşterea distanţei dintre conductori. Dacă distanţa dintre cei doi conductori creştere, capacitatea distribuită scade, datorită distanţei mai mare dintre armături, iar inductanţa distribuită creşte, datorită efectelor de anulare a câmpurilor magnetice opuse mult mai mici. O capacitate paralel mult mai mică, şi o inductanţă serie mult mai mare, duce la un curent mult mai mic prin linie pentru aceeiaşi valoare a tensiunii aplicate, ceea ce prin definiţie înseamnă o impedanţă mai mare. Invers, dacă distanţa dintre cei doi conductori scade, capacitatea paralel creşte, iar inductanţa serie scade. Rezultatul este un curent mai mare prin conductori pentru aceeiaşi valoare a tensiunii, ceea ce înseamnă de fapt o impedanţă mai mică.
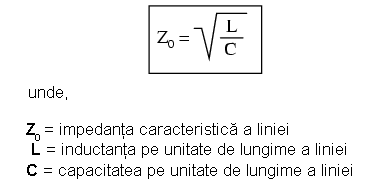
Ignorând orice efecte disipative a conductorilor, impedanţa caracteristică a liniilor electrice lungi este egală cu rădăcina pătrată a raportului dintre inductanţa liniei pe unitate de lungime şi capacitatea liniei pe unitate de lungime:
13.3 Linii electrice finite
O linie de transmisie inifită, precum cea considerată în secţiunea precedentă, este imposibil de realizat din punct de vedere fizic, prin urmare, comportamentul lor nu va fi exact acelaşi precum o linie infinită.
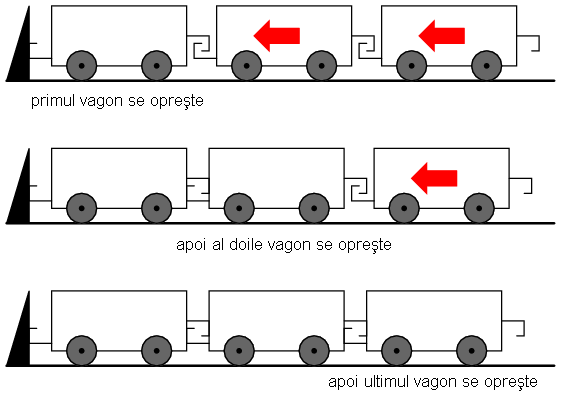
Totuşi, cunoaşterea/calcularea impedanţei caracteristice a liniilor de transmisie este importantă şi atunci când avem de a face cu lungimi finite. Dacă celălalt capăt al unei linii de transmisie finite este deschis, unda de curent ce se propagă în lungimea conductorului trebuie să se oprească la un moment dat, din moment ce electronii nu se pot deplasa într-un circuit deschis. Această întrerupere abruptă a curentului la sfârşitul liniei produce o „îngrămădire” de electroni de-a lungul liniei de transmisie, pentru că aceştia nu au unde să se deplaseze. Dacă ne imaginăm un tren lung în mişcare, cu o anumită cursă între vagoane, iar primul vagon (sau locomotiva) se opreşte brusc într-un parapet fix, acesta se va opri; urmarea este că toate celelalte vagoane din urma lui se vor opri rând pe rând, după ce fiecare parcurge „cursa” sa. Trenul nu se opreşte deodată, ci fiecare vagon pe rând, de la primul, până la ultimul:
Propagarea unui semnal de la sursă până la capătul unei linii de transmisie (spre sarcină), poartă numele de undă incidentă. Propagarea unui semnal de la sarcină (capătul liniei) spre sursă, poartă numele de undă reflectată
Această „îngrămădire” de electroni se propagă înapoi spre baterie, curentul prin baterie încetează, iar linia electrică se comportă precum un circuit deschis. Toate aceste lucruri au loc foarte repede pentru o linie de transmisie de lungime rezonabilă, prin urmare, un ohmetru nu poate măsură această perioadă foarte scurtă de timp în care linia se comportă precum un rezistor. Pentru o linie de aproximativ un kilometru, cu un factor de viteză de 0.66, durata de deplasare a semnalului de la un capăt la celălalt este de aproximativ şase microsecunde (3*10-6). Prin urmare, semnalul reflactat ajuge înapoi la sursă în aproximativ 12µs, după care, linia de transmisie se comportă precum un circuit deschis.
Există aparate ce pot măsura acest interval foarte scurt de timp de la sursă la capătul liniei şi înapoi, şi pot fi folosite pentru măsurarea lungimilor cablurilor. Această tehnică poate fi folosită şi pentru determinarea prezenţei şi locaţiei unei întreruperi într-unul sau în ambii conductori ai unei linii de transmisie, deoarece curentul se va „reflecta” din locul întreruperii la fel cu se reflectă şi într-un circuit deschis. Asfel de instrumente poartă numele de reflectometre, iar principiul de funcţionare este identic cu cel al sonarelor: generarea unui puls sonor şi măsurarea timpului necesar pentru întoarcerea ecoului.
Un fenomen similar are loc dacă scurt-circuităm capătul liniei de transmisie: când unda de tensiune ajunge la capătul liniei, acesta este reflectată înapoi spre sursă, deoarece tensiunea nu poate exista între două puncte comune din punct de vedere electric. Când unda reflectată ajunge înapoi la sursă, din punctul de vedere al sursei, întreaga linie de transmisie este scurt-circuitată. Din nou, acest lucru se întâmplă foarte repede.
Putem ilustra acest fenomen de reflexie al liniilor de transmisie cu un experiment simplu.
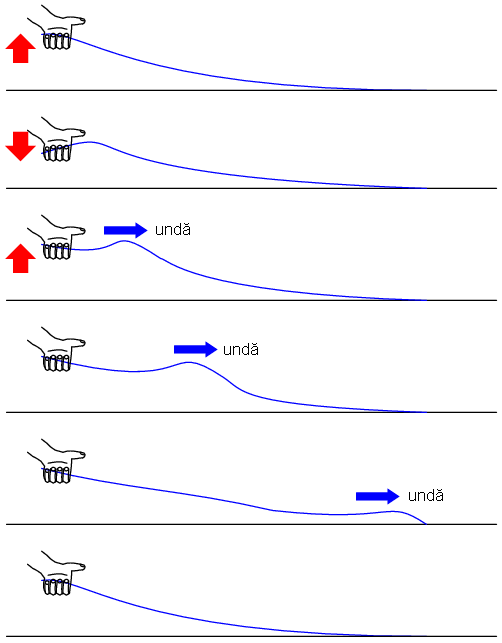
Acest lucru este analog unei linii de transmisie cu pierderi interne: puterea semnalului este din ce în ce mai slabă pe măsură ce se propagă în lungimea liniei şi nu se reflectă niciodată înapoi spre sursă. Totuşi, dacă celălalt capăt al sforii este fixat într-un punct în care amplitudinea semnalului nu este încă zero, în lungul sforii va apărea o a doua undă, reflectată înapoi spre mână.
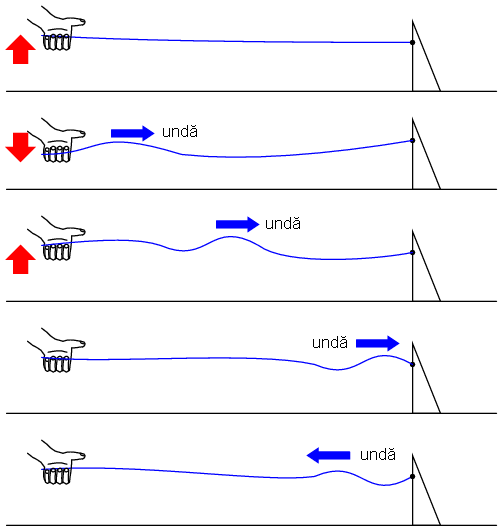
De obicei, rolul unei linii de transmisie este propagarea (transportul) energiei electrice dintr-un punct în altul. Dar chiar dacă semnalele sunt folosite doar pentru transmitere de informaţii, şi nu pentru alimentarea unei sarcini, situaţia ideală ar fi ca între semnalul original să fie transmis de la sursă spre sarcină şi abosorbit complet de aceasta, pentru un raport semnal/zgomot cât mai bun. Prin urmare, „pierderile” din lungul liniilor de transmisie sunt nedorite, la fel ca şi undele reflectate, deoarece energia reflectată reprezintă energie ce nu este transmisă sarcinii.
Eliminarea reflexiei liniilor de transmisie
Reflexiile liniilor de transmisie pot fi eliminate dacă impedanţa sarcinii este egală cu impedanţa liniei. De exemplu, un cablu coaxial de 50 Ω, ce este fie deschis, fie scurt-circuitat, va reflacta întreaga energie incidentă înapoi spre sursă. Dacă vom conecta însă un rezistor de 50 Ω la celălalt capăl al cablului, întreaga energia se va disipa pe acesta şi nu vor exista unde reflectate înapoi spre sursă.
În principiu, un rezistor a cărei impedanţă (rezistenţa) este exact impedanţa naturală (impedanţa caracteristică a liniei), conectat la capătul liniei de transmisie, face ca linia să „pară” infinit de lungă din punctul de vedere al sursei, deoarece un rezistor poate disipa energia pentru o durată infinită, în aceeiaşi măsură în care o linie de tansmisie infinită poate abosrbi energie pentru o durată de timp infinită.
În cazul în care rezistenţa nu este perfect egală cu impedanţa caracteristică a liniei de transmisie, vor apărea unde reflectate înapoi spre sursă, cel puţin parţial.
Se poate întâmpla ca unda reflectată să fie re-reflectată de către sursă, dacă impedanţa internă (impedanţa Thevenin echivalentă) a sursei nu este exact egală cu impedanţa caracteristică a liniei. O undă reflectată pe sursă va fi disipată în întregime, dacă impedanţa sursei este egală cu cea a liniei, dar va fi reflectată înapoi pe linie precum orice altă undă, cel puţin parţial, dacă impedanţa sursei nu este egală cu cea a liniei. Acest tip de reflexii pot fi supărătoare, deoarece aparent, reflexia undei de către sursă duce la impresia că aceasta tocmai a emis un puls nou.
13.4 Linii electrice lungi şi linii electrice scurte
În circuitele de curent continuu şi în cele de curent alternativ de frecvenţă joasă, impedanţa caracteristică a conductorilor paraleli este de obicei ignorată, datorită duratelor de timp relativ scurte a reflexiilor din lungul liniilor, faţă de perioada undelor sau a pulsurilor din circuit. După cum am văzut în secţiunea precedentă, dacă o linie de transmisie este conectată la o sursă de curent continuu, aceasta se va comporta precum un rezistor a cărei valoare este egală cu impedanţă caracteristică a liniei pentru o durată de timp egală cu durata de parcugere a undei până la capătul liniei şi înapoi spre sursă. După acea perioadă (aproximativ 12 µs pentru un cablu coaxial de un kilometru), sursa „vede” doar impedanţa conectată în circuit, oricare ar fi aceasta.
Dacă circuitul în cauză foloseşte putere în curent alternativ, consecinţele unei asemenea întârzieri, introduse de linia de transmisie între vârful tensiunii de curent alternativ generat de tensiune şi momentul în care sarcina „vede” acest vârf, nu sunt de o importanţă crucială. Cu toate că amplitudinile instantanee ale semnalului în lungimea liniei nu sunt egale, datorită propagării acestuia cu viteza luminii, diferenţa de fază a semnalelor dintre începutul şi capătul liniei este neglijabilă, deoarece propagarea acestora în lungul liniilor au loc cu o fracţiune foarte mică din perioada formei de undă alternative. Din considerente practice, putem spune că tensiunea de-a lungul unei linii de transmisie cu două conductoare, de frecvenţă joasă, este egală şi în fază în oricare moment.
Acest tip de line poartă denumirea de linie de transmisie scurtă, deoarece efectele propagării semnalelor sunt mult mai rapide decât perioadele semnalelor transmise. Invers, o linie electrică lungă are un timp de propagare mult mai mare ce poate ajunge să fie multiplu al perioadei semnalului transmis. O linie este considerată „lungă” atunci când semnalul sursei „parcurge” cel puţin un sfert de perioadă (90 de grade) înainte ca semnalul incident să ajungă la capătul liniei. Până în acest moment, toate liniile electrice au fost considerate electric scurte.
Să încercăm o explicaţie. Trebuie să exprimăm distanţa parcursă de o undă de tensiune sau curent, în lungul liniei de transmisie, în funcţie de frecvenţa sursei. Perioada unei forme de undă alternative cu o frecvenţă de 60 Hz este de 16,66 ms. La viteza luminii, un semnal de tensiune sau curent va parcurge o distantă de aproximativ 5 km. Dacă factorul de viteză al liniei de transmisie este sub unu, viteza de propagare va fi mai mică decât viteza luminii, prin urmare şi distanţa parcursă va fi mai mică. Dar chiar şi dacă utilizăm un factor de viteză mai mică, distanţa parcusă în acel interval va fi tot foarte mare. Distanţa calculată pentru o anumită frecvenţa, poartă denumirea de lungime de undă a semnalului.
Formula de calcul a lungimii de undă este următoarea:

Considerând o linie lungă ca având o lungime de cel puţin 1/4 din lungimea de undă, putem vedea de ce toate liniile folosite în circuitele discutate au fost presupuse ca fiind linii electrice scurte. Pentru un circuit la frecvenţa de 60 Hz, liniile de tensiune ar trebui să depăşească 1.200 de kilometri în lungime, înainte ca efectele timpului de propagare a semnalelor să devină importante. Cablurile ce realizează conexiunea dintre difuzoare şi amplificator ar trebui să depăşească lungimea de 7 kilometri pentru ca reflexiile acestuia să afecteze suficient de mult semnalul audio de 10 kHz.
În cazul circuitelor de frecvenţă înaltă însă, lungimea liniei este foarte importantă. Să considerăm ca şi exemplu un semnal radio de 100 MHz, lungimea sa de undă fiind de doar 3 m, chiar şi la viteza de propagare maximă (factor de viteză 1). O linie de transmisie pentru acest semnal este considerată lungă dacă depăşeşte lungimea de 0.75 m! Mai mult, cu un factor de viteză de 0.66, această lungime critică devine 0.5 m!
Când o sursă electrică este conectată la sarcină printr-o linie de transmisie scurtă, impedanţa sarcinii domină circuitul. Cu alte cuvinte, când linia electrică este scurtă, impendaţa caracteristică a liniei are un impact extrem de redus asupra performanţelor circuitului.
La conectarea unei surse la sarcină prin intermediul unei linii de transmisie lungă, impedanţa caracteristică a liniei domină impedanţa sarcinii. Cu alte cuvinte, liniile electrice lungi constituie componenta principală a circuitului.
Cea mai eficientă metodă de minimizare a impactului lungimii liniilor de transmisie asupra circuitului, este egalarea impedanţei caracteristice a liniei cu impedanţa sarcinii. În acest caz, orice sursă de semnale conectată la celălalt capăt al iniei va „vedea” exact aceeiaşi impedanţă, şi va genera acelaşi curent în circuit, indiferent de lungimea liniei. În această condiţie perfectă, lungimea liniei afectează doar durata de timp necesară pentru transmiterii semnalului de la sursă la sarcină. Totuşi, egalarea perfectă a impedanţelor nu este tot timpul practică sau posibilă.
13.5 Unde staţionare şi rezonanţa
De câte ori există o diferenţă între impedanţa caracteristică a liniei şi impedanţa sarcinii, vor apărea şi reflexii ale undelor. Dacă unda incidentă este o formă de undă alternativă, aceste reflexii se vor „amesteca” cu semnalele incidente, iar formele de undă produse poartă numele de forme de undă staţionare.
Următoarea ilustraţie exemplifică modul în care o undă incidentă triunghiulară se transformă într-o reflexie „în oglindă” după ce aceasta ajunge la capătul liniei de transmisie (întrerupte). Linia de transmisă este reprezentată în acest caz doar printr-o singură linie, pentru simplitate. Unda incidentă se deplasează de la stânga la dreapta, iar unda reflectată de la dreapta la stânga:
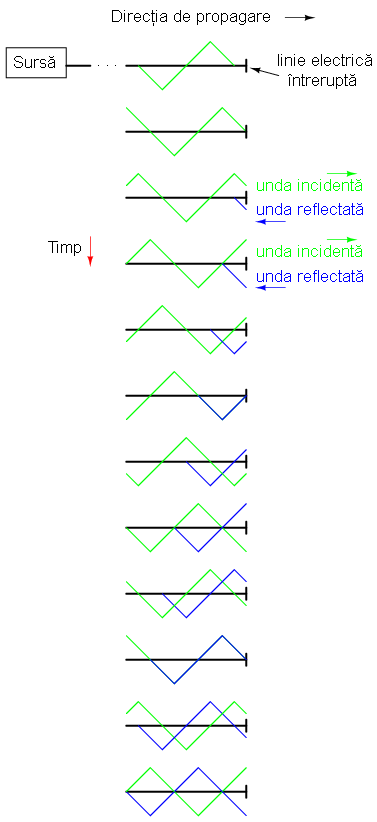
Dacă adăugăm cele două forme de undă, descoperim că în lungul liniei se formează de fapt o a treia formă de undă, staţionară:
linie electrică întreruptă; formarea formei de undă staţionare ca sumă

Cea de a treia undă, cea staţionară, reprezintă de fapt singura tensiune din lungul liniei, fiind suma undelor incidente şi a undelor reflectate. Amplitudinea sa instantanee oscilează, dar unda nu se propagă în lungimea liniei precum celelalte două forme de undă. De observat că punctele de pe linie, ce marchează amplitudinea zero a undei staţionare (locul în care unda incidentă şi cea reflectată se anulează reciproc), au tot timpul aceeiaşi poziţie:
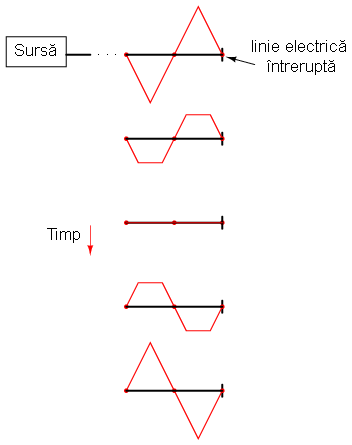
Undele staţionare sunt destul de frecvent întâlnite în lumea înconjurătoare. Să considerăm o coardă, legată la un capăt şi „scuturată” la celălalt:
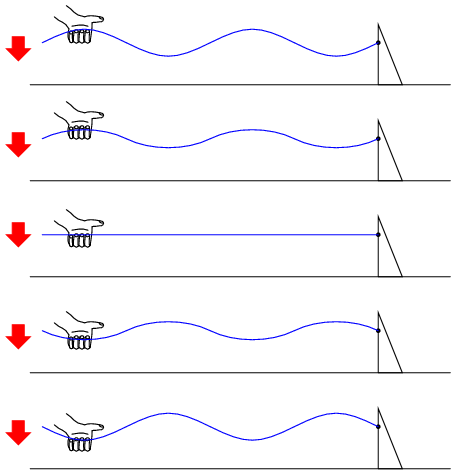
Atât nodurile (punctele unde vibraţia este foarte mică sau inexistentă), cât şi antinodurilor (punctele unde vibraţia este maximă) rămân fixe de-a lungul corzii. Efectul este şi mai pronunţăt când capătul liber este mişcat la frecvenţa corectă. Corzile fixe prezintă acelaşi comportament. Diferenţa majoră este că aceasta vibrează la frecvenţa sa „corectă” pentru maximizarea efectului undelor staţionare: