< Curent alternativ

2 Numerele complexe

2.1 Introducere

Dacă dorim de exemplu să descriem distanţa dintre două oraşe, putem folosi o singură cifră, în kilometri, sau orice altă unitate de măsură pentru distanţa liniară. Totuşi, dacă vrem să descriem şi modul de deplasare dintr-un oraş în altul, avem nevoie de mai multă informaţie pe lângă distanţă propriu-zisă dintre oraşe; trebuie să indicăm şi direcţia de mers în acest caz.

Tipul de informaţie ce exprimă o singură dimensiune, precum distanţa liniară, poartă denumirea de scalar în matematică. Numerele scalare sunt cele folosite pentru desemnarea valori tensiunii unei bateri, de exemplu, a rezistenţei sau a curentului, dacă vorbim de curent continuu.

Totuşi, atunci când începem să analizăm circuitele electrice în curent alternativ, descoperim că valorile tensiunii, curentului şi chiar a rezistenţei (denumită impedanţă în curent alternativ) nu sunt cantităţi uni-dimensionale precum în cazul circuitelor de curent continuu, ci, aceste cantităţi, fiind dinamice (alternează în direcţie şi amplitudine), posedă alte dimensiuni ce trebuiesc luate în considerare. Frecvenţă şi diferenţă de fază sunt două dintre aceste dimensiuni adiţionale.

Pentru a putea analiza cu succes circuitele de curent alternativ, trebuie să abandonăm numerele scalare şi să luăm în considerare cele complexe, capabile să reprezinte atât amplitudine cât şi faze unei unde în acelaşi timp.

Numerele complexe sunt mai uşor de înţeles dacă sunt trecute pe un grafic. Dacă desenăm o linie cu o anumită lungime (amplitudine) şi unghi (direcţie), obţinem o reprezentare grafică a unui număr complex, reprezentare cunoscută în fizica sub numele de vector:

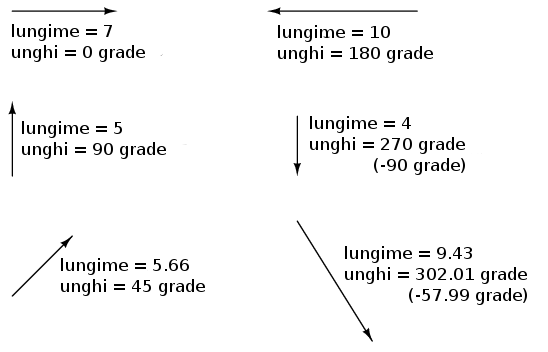
Precum în cazul distenţelor şi direcţiilor de pe o hartă, trebuie să avem un sistem de referinţă pentru ca toate aceste valori să aibă un sens. În acest caz, dreapta înseamnă 0^o, iar unghiurile sunt măsurate în direcţie pozitive în sensul invers acelor de ceasornic:

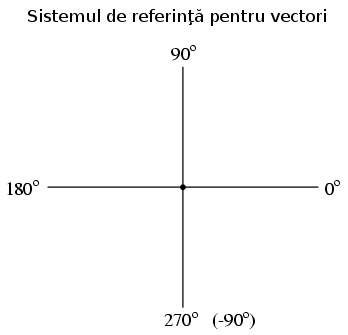
2.2 Vectori şi forme de undă în curent alternativ

Să luăm câteva exemple de reprezentare a formelor de undă în curent alternativ cu ajutorul vectorilor, unde lungimea vectorului reprezintă amplitudinea undei, asfel:

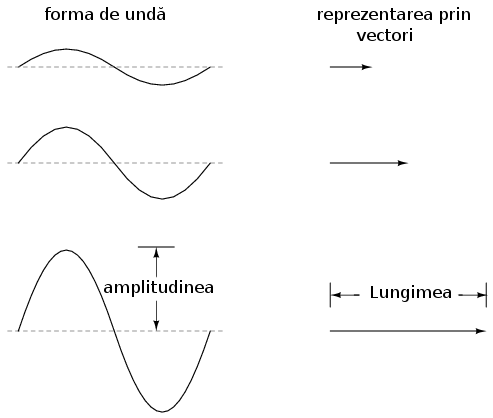
Cu cât amplitudinea formei de undă este mai mare, cu atât lungimea vectorului corespunzător va fi mai mare. Unghiul vectorului, pe de altă parte, reprezintă diferenţa de fază (defazajul) dintre unda considerată si o altă formă de undă de referinţă. De obicei, atunci când exprimăm faza unei forme de undă, punctul de referinţă îl reprezintă forma de undă a sursei de alimentare, considerată a fi O^o. Ţineţi minte că faza este tot timpul o mărime relativă dintre două unde şi nu o proprietate absolută a undelor.

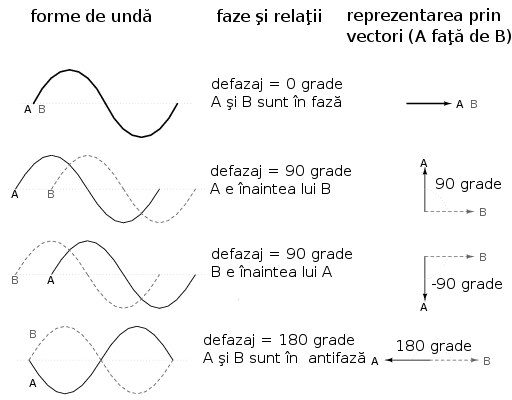
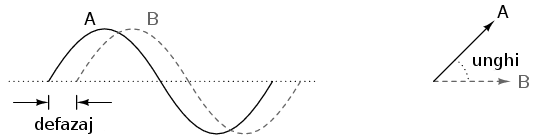
Cu cât defazajul dintre formele de undă considerate este mai mare, cu atât este mai mare unghiuld dintre vectorii corespunzători.

2.3 Adunarea simplă a vectorilor

Operaţiile ce pot fi efectuate asupra vectorilor sunt aceleaşi care sunt posibile asupra oricărei mărimi scalare: adunare, scădere, înmulţire, împărţire. Dintre toate acestea, adunarea este probabil cea mai uşor de înţeles. Dacă adunăm doi vectori ce au acelaşi unghiu, lungimile lor se adună precum o mărime scalară:

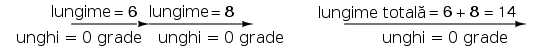
Similar, dacă două sau mai multe surse de curent alternativ cu aceeiaşi fază sunt conectate în serie, tensiunile lor se adună asemenea tensiunilor bateriilor:

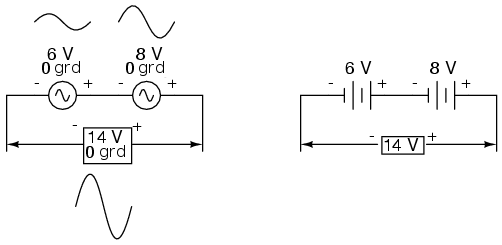
Observaţi notaţia „+” şi „-” la bornele surselor de alimentare în curent alternativ. Chiar dacă noţiunea de polaritate nu este aceeiaşi precum în curent continuu, aceste notaţii sunt esenţiale pentru scoaterea în evidenţă a fazei undei de referinţă (tensiunea).

Dacă adunăm doi vectori, a căror diferenţe de fază este de 180^o, aflaţi prin urmare în opoziţie, lungimile lor se scad, asemenea operaţiei de adunare dintre doi scalari, unul pozitiv şi celălalt negativ:

În mod similar, dacă două surse de curent alternativ aflate în antifază (defazaj de 180^o sunt conectate în serie, tensiunile lor se scad asemenea bateriilor de curent continuu conectate în opoziţie:

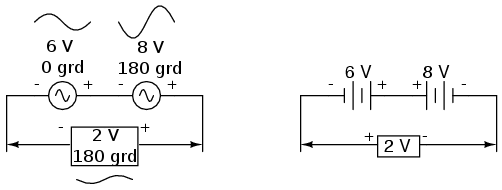
Pentru a determina dacă cele două surse se află în opoziţie una faţă de celalată, este nevoie de o examinare atentă atât a polarităţii (+ sau -) cât şi a fazelor. Polarităţile de mai sus tind să indice faptul că cele două tensiuni sunt aditive (de la stânga spre dreapta: - şi + la sursa de 6 V, - şi + la sursa de 8 V). Chiar dacă aceste notaţii ar indica în mod normal un efect aditiv într-un circuit de curent continuu (cele două tensiuni „lucrează” împreună pentru a produce o tensiune rezultată mai mare), în acest circuit de curent alternativ, cele două tensiuni se scad pentru a da tensiunea finală, deoarece faza uneia dintre ele este de 0^o, iar a celeilalte de 180^o. Rezultatul total este o tensiune de 2 V, la 180^o, sau, -2 V la 0^o.

Un alt exemplu în care tensiunile se scad este următorul:

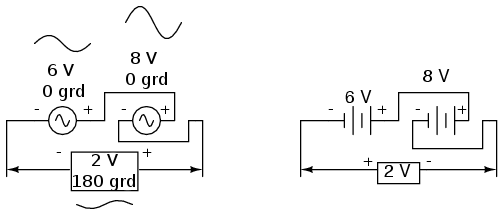
După cât am văzut mai sus, există două moduri de reprezentare a rezultatului final:

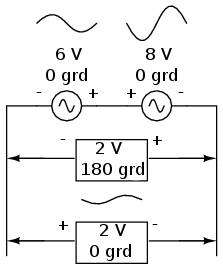
O inversare a firelor sursei de curent alternativ este echivalentă cu schimbarea fazei acelei surse cu 180 de grade:

2.4 Adunarea complexă a vectorilor

Dacă adunăm doi vectori cu unghiuri diferite, lungimile lor se adună diferit faţă de cele scalare:

Dacă două tensiuni alternativ, defazate cu 90^o între ele, sunt conectate în serie, amplitudinile lor nu se adună sau scad direct precum valorile scalare în cazul curentului continuu. În schimb, aceste tensiuni sunt valori complexe, şi, precum în cazul vectorilor de mai sus a căror adunare se realizează trigonometric, o sursă de 6 V la 0^o adunată (conectată în serie) cu o sursă de 8 V la 90^o, rezultă într-o tensiune de 10 V a cărei fază este de 53.13^o:

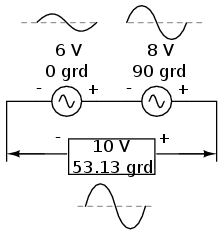
Prin comparaţie cu circuitele de curent continuu, acest lucru poate părea ciudat la început. De exemplu, cu ajutorul unui voltmetru, putem citi indicaţiile de 6 şi respectiv 8 volţi la borenele celor două surse de curent alternativ, dar tensiunea totală indicată de acesta va fi de „doar” 10 volţi!

2.5 Notaţia polară şi rectangulară a numerelor complexe

Pentru a putea lucra cu aceste numere complexe fără a fi nevoiţi să desenăm tot timpul vectori, avem nevoie de o notaţie matematică standard. Există două forme pentru notaţia numerelor complexe: polară şi rectangulară.

Notaţia polară

Forma polară constă în exprimarea unui număr complex prin lungimea (cunoscută şi sub numele de dimensiune, valoare absolută, modul) şi unghiul vectorului (desemnat de obicei prin simbolul ∠). Să luăm două exemple de vectori împreună cu notaţia lor polară:

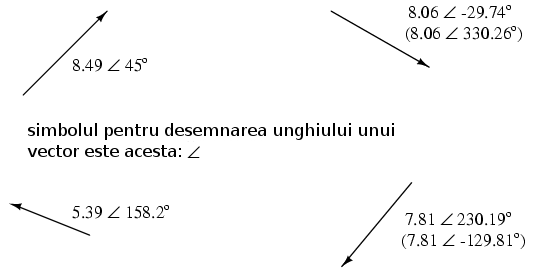
Orientarea standard pentru unghiurile vectorilor în curent alternativ defineşte unghiul de 0 grade ca fiind în dreapta (axa orizontală), 90^o sus, 180^o stânga, 270^o jos. Atenţie, vectorii a căror unghi este „în jos” pot fi reprezentaţi cu ajutorul notaţiei polare ca fiind vectori pozitivi cu un unghi de peste 180^o, sau ca numere negative cu unghiuri sub 180^o. De exemplu, putem spune că un vector cu unghiul ∠270^o (direct în jos) are unghiul de -90^o (notaţie echivalentă). Vectorul de mai sus (7.81 ∠230.19^o) poate fi descris de asemenea prin 7.81 ∠-129.81^o.

Notaţia rectangulară

Forma rectangulară constă în reprezentarea vectorului prin componentele sale orizontale şi verticale. În esenţă, vectorului unghiular este considerat a fi ipotenuza unui unghi drept şi descris cu ajutorul lungimilor laturilor opuse respectiv adiacente. În loc să descrie lungimea şi direcţia unui vector prin precizarea lungimii şi a unghiului, acesta este descris în termenii „cât de departe în stânga/dreapta” şi „cât de departe „sus/jos”.

Aceste două valori dimensionale (orizontală şi verticală) sunt simbolizate prin două valori numerice. Pentru a putea face distincţie între cele două dimensiuni, cea verticală este însoţită de notaţia „i” (în matematica pură) sau „j” (în domeniul electric). Aceste litere nu reprezintă o variabilă fizică (precum curentul instantaneu, simbolizat de asemenea prin „i”), ci sunt operatori matematici folosiţi pentru a face distincţia dintre componenta verticală şi cea orizontală a unui vector. Ca şi număr complex complet, valorile cele două componente sunt scrise ca şi sumă:

Componenta orizontală este denumită componentă reală deoarece aceasta este compatibilă cu numerele normale, scalare („reale”). Componenta verticală este denumită componenta imaginară, deoarece această dimensiune se află pe o altă direcţie şi nu are nicio legătură cu scara numerelor reale.

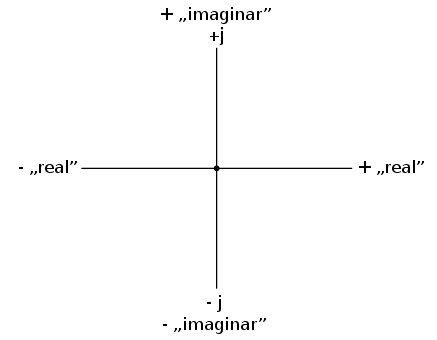
Cele două axe poartă denumirea de axa reală respectiv axa imaginară:

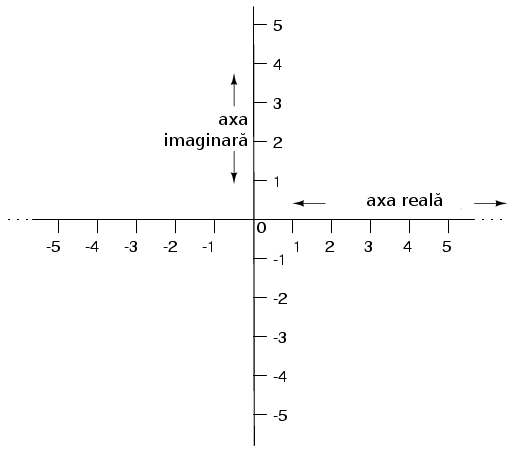
Oricare dintre cele două forme poate fi folosită pentru numerele complexe. Principalul motiv pentru care există două sisteme de notaţie valide se datorează faptului că forma rectangulară este uşor de folosit pentru adunare şi scădere, iar forma polară pentru înmulţire şi împărţire.

Transformarea din formă polară în formă rectangulară

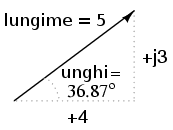
Transformarea din formă rectangulară în formă polară

Pentru a realiza conversi de la forma rectangulară la cea polară, găsim mai întâi lungimea polară folosind teorema lui Pitagora, fiindcă lungimea polară este ipotenuza unui triunghiu dreptunghic, iar componenta reală şi cea imaginară sunt reprezentate de latura adiacentă respectiv cea opusă. Găsim unghiul ca fiind raportul dintre arctangenta componentei imaginare şi componenta reală:

2.6 Aritmetica numerelor complexe

Adunarea numerelor complexe

Pentru adunarea numerelor complexe, adunăm pur şi simplu componentele reale pentru a determina componenta reală a sumei cele două numere complexe; acelaşi lucru este valabil şi pentru componenta imaginară:

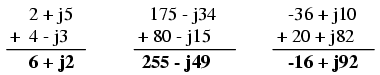
Scăderea numerelor complexe

Pentru scăderea numerlor complexe, se aplică acelaşi principiu de mai sus, doar cu scădere în loc de adunare:

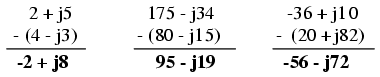
Înmulţirea numerelor complexe

Pentru operaţiile de înmulţire şi împărţire forma preferată este cea polară. Atunci când efectuăm înmulţirea numerelor complexe sub formă polară, înmulţim pur şi simplu dimensiunile numerelor complexe pentru determinarea dimensiuni produsului şi adunăm unghiurile numerelor complexe pentru determinarea unghiului final al produsului:

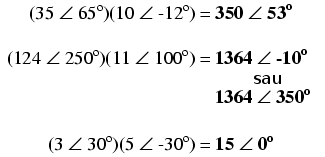
Împărţirea numerelor complexe

Pentru efectuarea împărţirii numerelor complexe, calculăm pur şi simplu raportul dintre dimensiunea primului număr complex cu dimensiunea celui de al doilea pentru aflarea dimensiunii final a raportului, şi scădem unghiul celui de al doilea număr complex din primul pentru a afla unghiul final al raportului dintre cele două numere complexe:

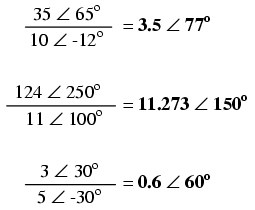
Reciproca (inversa) numerelor complexe

Pentru a obţine reciproca (1/x), sau inversa unui număr complex, calculăm raportul dintre valoarea scalară 1 (unghi zero) şi numărul complex sub formă polară:

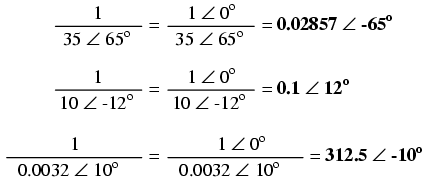
2.7 Clarificări legate de polaritatea curentului alternativ

2.7.1 Polaritatea căderilor de tensiune

Numerele complexe sunt folositoare pentru analiza circuitelor de curent alternativ, deoarece reprezintă o metodă comodă de reprezentare simbolică a defazajului dintre mărimile curentului alternativ, precum tensiunea şi curentul. Totuşi, pentru majoritatea dintre noi, echivalenţa dintre abstractizarea vectorială şi valorile reale dintr-un circuit este destul de greu de înţeles. În acest capitol, am văzut că sursele de tensiune de curent alternativ sunt caracterizate atât prin valoarea tensiunii sub formă complexă (amplitudine şi unghi de fază) cât şi prin polaritatea tensiunii. Dat fiind faptul că în cazul curentului alternativ nu există o „polaritate” dată, precum în cazul curentului continuu, aceste notaţii de polaritate şi relaţia acestora cu unghiul de fază poate crea confuzii. Această secţiune este scrisă pentru a încerca clarificarea unora dintre aceste probleme.

Tensiunea este o cantitate relativă. Atunci când măsurăm o tensiune, putem alege modul de conectare a voltmetrului la sursa de tensiune, din moment ce există două puncte între care măsurăm tensiunea şi două sonde pentru oricare voltmetru. În cazul circuitelor de c.c., polaritatea şi valoarea surselor de tensiune se specifică exact folosind simbolurile „+” şi „-”. În cazul sondelor aparatului de măsură, acestea sunt colorate cu roşu, respectiv negru. Dacă un voltmetru digital indică o tensiune de c.c. negativă, putem fi siguri că sondele de test au fost conectate invers (roşu la „-” şi negru la „+”).

Polaritatea bateriilor este specificată prin intermediul simbolisticii specifice acestora: linia mai scurtă reprezintă tot timpul terminalul negativ (-), iar linia orizontală mai lungă este tot timpul borna pozitivă (+):

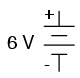
Cu toate că, din punct de vedere matematic, reprezentarea tensiunii bateriei printr-o valoare negativă şi polaritatea bornelor inversată este corectă, acest lucru nu este convenţional:

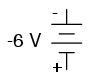
Interpretarea unei astfel de notaţii ar fi mai usoară dacă polarităţile „+” şi „-” ar fi văzute ca şi puncte de referinţă pentru sondele voltmetrului. Polaritatea „+” însemnând „roşu” iar „-” însemnând „negru”. Un voltmetru conectat la bateria de mai sus cu sonda roşie la borna de jos şi sonda neagră la borna de sus, ar indica într-adevăr o tensiune negativă (-6 V).

În cazul circuitelor de c.a. totuşi, nu lucrăm cu valori negative ale tensiunii. În schimb, descriem relaţia dintre două tensiuni prin intermediul fazei: defazarea în timp dintre două forme de undă. Nu descriem niciodată o tensiune de c.a. printr-o valoare negativă, deoarece utilizarea notaţiei polare permite existenţa vectorilor cu sens invers. Dacă două tensiuni de c.a. sunt opuse (+6 V şi -6 V pentru c.c.), spunem că ele sunt defazate cu 180⁰ între ele, sau că se găsesc în antifază.

Totuşi, tensiunea este o valoare relativă între două punce, şi putem alege modul de conectare a aparatului de măsură între aceste două puncte. Semnul matematic al indicaţiei unui voltmetru în cazul unei măsurători în c.c. are sens doar în contextul modului de conectare al celor două sonde (la care terminal este conectată sonda roşie, şi la care terminal cea neagră). Asemănător, unghiul de fază a unui semnal de c.a are sens doar dacă ştim care din cele două puncte este considerat punctul de „referinţă”. Din această cauză, polarităţile „+” şi „”¨sunt adesea folosite pentru bornele surselor de c.a.: pentru a specifica punctul de referinţă al unghiului de fază. p>