< Curent alternativ
4 Reactanta capacitiva
4.1 Circuite pur rezistive
Vezi subcapitolul precedent (3.1)
4.2 Circuite pur capacitive
Comportamentul condensatoarelor este diferit faţă de cel al rezistorilor. Pe când rezistorii opun o rezistenţă direct proporţională cu căderea de tensiune în faţă curgerii curentului, condensatoarele se opun variaţiei de tensiune absorbând (încărcare) sau eliberând (descărcare) curent în circuit. Curgerea curentului „prin” condensator este direct proporţională cu rata de variaţie a tensiunii la bornele acestuia. Această opoziţie în calea variaţiei tensiunii este o altă formă de reactanţă, opusă însă reactanţei bobinei.
Matematic, relaţia dintre curentul condensatorului şi rata de variaţie a tensiunii la bornele acestuia, se exprimă asfel:
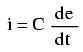
Expresia de/dt exprimă rata de variaţie a tensiunii instantanee (e) în raport cu timpul, calculată în volţi per secundă. Capacitatea (C) este în Farazi, iar curentul instantaneu (i) în Amperi. O exprimare echivalentă este şi dv/dt, folosind „v” în loc de „e” pentru exprimarea tensiunii; cele două notaţii sunt însă echivalente. Să analizăm un circuit simpul pur capacitiv:
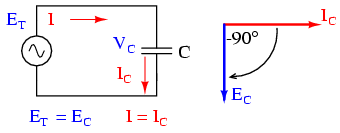
În circuitul de mai sus, tensiunea este defazată în urma curentului cu 90o. Graficul celor două forme de undă arată asfel:
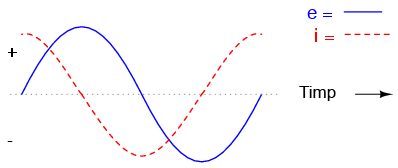
Reţineti, curentul printr-un condensator este rezultatul variaţiei tensiunii la bornele acestuia. Prin urmare, curentu instantaneu este zero atunci când tensiunea instantanee este la valoarea sa maximă, pozitivă sau negativă, reprezentând variaţie zero sau pantă zero; curentul instantaneu are valoarea maximă atunci când tensiunea instantanee are variaţia maximă, adică zona în care variaţia este maximă (intersecţia cu axa orizontală a timpului). Rezultă o undă a tensiunii defazată cu -90o faţă de curent. Dacă ne uităm pe grafic, curentul pare să aibe un „avantaj” faţă de tensiune; curentul este defazat înaintea tensiunii, sau echivalent, tensiunea este defazată în urma curentului.
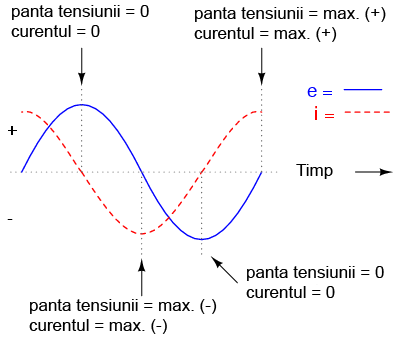
Forma de undă pentru putere este asemănătoare celei existente în cazul circuitului pur inductiv:
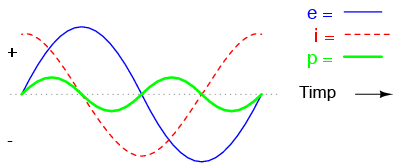
Defazajul de 90o dintre curent şi tensiune duce la o formă a undei de putere ce alternează în mod egal între pozitiv şi negativ. Aceast lucru înseamnă că nu există pierdere de putere (nu se disipă putere) pe condensator ca urmare a variaţiei tensiunii; acesta doar absoarbe putere şi apoi o eliberează din şi înspre circuit, în mod alternativ.
Opoziţia condensatorului la variaţia tensiunii se traduce printr-o opoziţia faţă de tensiunea alternativă în general, care prin definiţie îşi modifică tot timpul amplitudinea instantanee şi direcţia. Oricare ar fi amplitudinea tensiunii alternative pentru o anumită frecvenţă, un condensator va „conduce” o anumită valoare a curentului alternativ. La fel ca în cazul rezistorilor, unde curentul este o funcţie de tensiune la bornele acestuia şi rezistenţa sa, curentul alternativ printr-un condensator este o funcţie de tensiune la bornele sale şi reactanţa oferită de acesta. Ca şi în cazul bobinelor, reactanţa este exprimată în ohmi, iar simbolul este X (sau mai exact, XC - reactanţa capacitivă).
Din moment ce condensatoarele „conduc” curent în proporţie directă cu variaţia tensiunii, acestea vor conduce mai mult curent cu cât variaţia tensiunii este mai mare (durata de încărcare şi descărcare la valorile de vârf este mai mică), şi mai puţin cu cât variaţia tensiunii este mai mică. Acest lucru înseamnă că reactanţă condensatoarelor este invers proporţională cu frecvenţă curentului alternativ.
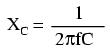
Reactanţă unui condensator de 100 µF:
| Frecvenţa (Hertz) | Reactance (Ohm) |
|---|---|
| 60 | 26.5258 |
| 120 | 13.2629 |
| 2500 | 0.6366 |
De observat că relaţia dintre reactanţa capacitivă şi frecvenţă este exact opusă faţă de cea a reactanţei inductive. Reactanţa capacitivă scade odată cu creşterea frecvenţei curentului alternativ, şi invers. Bobinele se opun variaţiei curentului prin producerea unor căderi de tensiune mai mari; condensatoarele se opun variaţiei tensiunii prin trecerea unor curenţi mai mari prin aceştia.
Termenul 2πf poate fi înlocuit cu litera grecească Omega (ω), viteza unghiulară a circuitului de curent alternativ. Asfel, ecuaţia XC = 1/(2πfC) devine XC = 1/(ωC), unde ω se exprimă în radiani pe secundă.
Curentul alternativ într-un circuit pur capacitiv este egal cu raportul dintre tensiune şi reactanţă capacitivă. Să luăm ca şi exemplu următorul circuit:
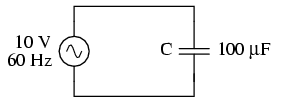
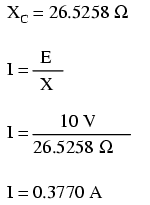
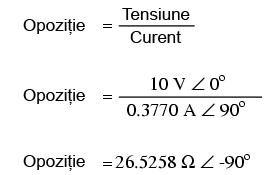
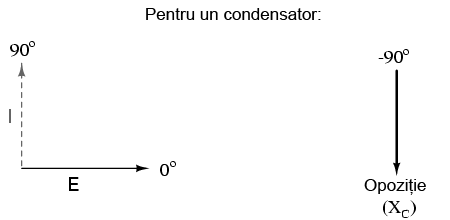
Totuşi, trebuie să ne reamintim faptul că tensiunea şi curentul nu sunt în fază în acest caz, curentul fiind defazat cu +90o faţă de tensiune. Dacă reprezentăm unghiul de fază al tensiunii şi al curentului sub formă matematică, putem calcula unghiul de fază al opoziţiei reactive a condensatorului faţă de curent:
4.3 Circuite rezistiv-capacitive serie
Până acum am văzut doar ce se întâmplă într-un circuit pur rezistiv, respectiv pur inductiv. Acum vom analiza cele două componente conectate împreună într-un circuit serie:
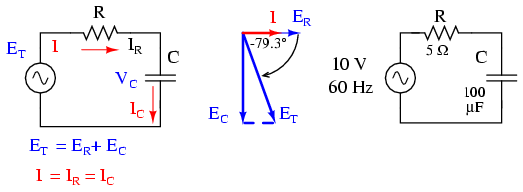
Rezistorul va produce o rezistenţă de 5 Ω în circuit faţă de curentul alternativ, indiferent de valoarea frecvenţei, iar condensatorul va produce o reactanţă de 26.5258 Ω faţă de curetul alternativ la o frecvenţă de 60 Hz. Deoarece rezistenţa rezistorului este un număr real (5 Ω ∠ sau 5 + j0 ∠ Ω), iar reactanţa condensatorului este un număr imaginar (26.5258 Ω ∠-90o sau 0 - j26.5258 Ω), efectul celor două componente luate împreună (combinate) va fi o opoziţie faţă de curent egală cu suma complexă a celor două numere. Termenul folosit pentru desemnarea acestei opoziţii faţă de curent se numeşte impedanţă, simbolizată prin Z şi exprimată în Ohm, la fel ca rezistenţă şi reactanţa. În circuitul de sus, impedanţă totală a circuitului este:

Relaţia dintre impedanţă, curent şi tensiune este similară rezistenţei din legea lui Ohm:

De fapt, această expresie este o formă a legii lui Ohm mult mai cuprinzătoarea (mai generală) decât cea considerată în curent continuu (E=IR), la fel precum impedanţă este o expresie mult mai cuprinzătoare a opoziţiei faţă de deplasarea electronilor decât rezistenţa. Orice rezistenţă şi orice reactanţă, separate sau în combinaţii serie/paralel, pot fi şi trebuie exprimate ca şi o singură impedanţă într-un circuit de curent alternativ.
Pentru a calcula curentul din circuitul de mai sus, trebuie să luăm prima data o referinţă a unghiului de fază pentru sursa de tensiune; în mod normal aceasta se consideră zero.
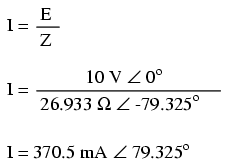
Ca şi în cazul circuitului pur capacitiv, curentul este defazat înaintea tensiunii (sursei), cu toate că de data aceasta diferenţa este de 79.325o, nu 90o.
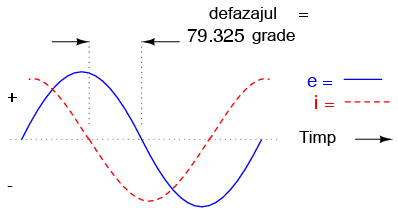
Să folosim din nou metoda tabelului pentru analiza circuitului de mai sus. Primul pas este introducerea tuturor cantităţilor cunoscute în tabel:
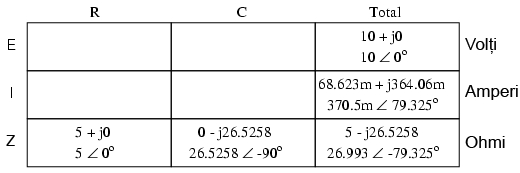
Într-un circuit serie, curentul total este acelaşi prin toate componentele circuitului; prin urmare, valorile curentului din coloana „Total” pot fi trecute şi în celelalte două coloane, a rezistorului şi a condensatorului:
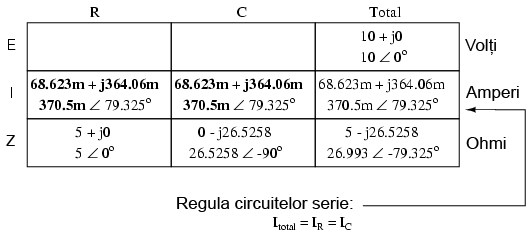
Continuând analiza, putem aplica legea lui Ohm (E=IR) vertical, pentru determniarea căderilor de tensiune pe rezistor şi condensator:
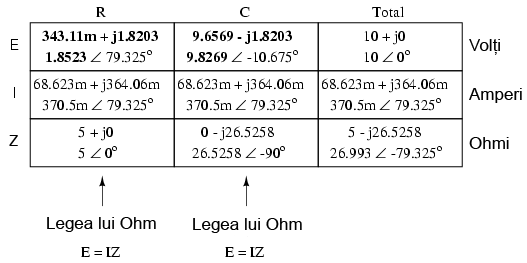
Observaţi faptul că tensiune şi curentul prin rezistor au acelaşi unghi de fază, ceea ce înseamnă că E şi I sunt în fază în cazul rezistorului. Tensiunea la bornele condensatorului are un unghi de fază de -10.675o, cu exact 90o mai puţin decât unghiul de fază al curentului din circuit. Acest lucru ne spune că tensiunea şi curentul condensatorului sunt defazate cu exact 90o între ele (în cazul condensatorului!).
Indicaţia instrumentelor de măsură
Din nou, trebuie să insistăm pe faptul că valorile calculate ce corespund cu măsurătorile reale luate de aparatele de măsură, sunt cele sub formă polară, nu rectangulară! De exemplu, dacă am construi fizic acest circuit rezistiv-capacitiv (R-C) şi am măsura tensiunea la bornele rezistorului, voltmetrul ar indica 1.8523 V, nu 343.11 mV (termenul real rectangular) şi nici 1.8203 V (termenul imaginar rectangular). Instrumentele reale de măsură conectate la circuite reale indică lungimea vectorului (magnitudinea). Notaţia rectangulară, deşi este mai uşor de folosit pentru operaţiile aritmetice de adunare şi scădere, este o formă de notaţia mai abstractă decât forma polară pentru măsurătorile reale. Dacă ar fi să folosim doar o singură notaţie, cea mai bună alegere ar fi cea polară, pentru că este singura ce are legătură directă cu măsurătorile reale.
Diagrama impedanţei
Impedanţa (Z) unui circuit serie R-L poate fi calculată cunoscând rezistenţă (R) şi reactanţa inductivă (XL). Din moment ce E=IR, E=IXL şi E=IZ, rezistenţa, reactanţa şi impedanţă sunt proporţionale cu tensiunea. Prin urmare, diagrama fazorială a tensiunii poate fi înlocuită cu o diagramă similară a impedanţei:
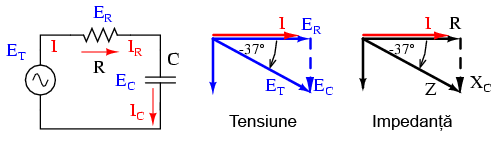
Exemplu
Găsiţi impedanţă unui circuit serie format dintr-un rezistor de 40 Ω şi un condensator de 88.42 mF la frecvenţa de 60 Hz. Răspuns: Z = 40 - j30 = 50∠36.87o.
4.4 Circuite rezistiv-capacitive paralel
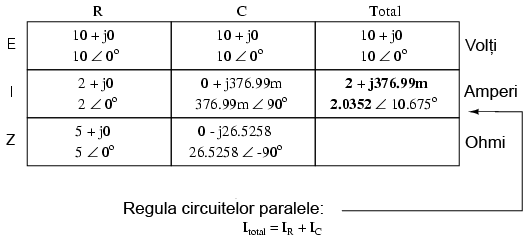
Folosind aceleaşi valori, vom conecta rezistorul şi condensatorul în paralel, şi vom trece la analiza acestuia folosind metoda tabelului:
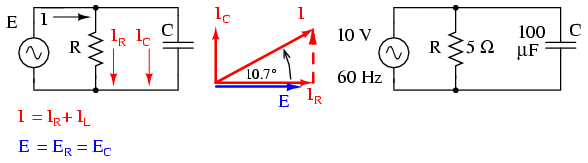
Întrucât sursa de tensiune are aceeiaşi frecvenţă ca şi în cazul circuitului serie, iar rezistorul şi condensatorul au aceleaşi valori ale rezistenţei, respectiv capacităţii, valorile impedanţelor trebuie să fie aceleaşi. Prin urmare, putem începe completarea tabelului cu valorile cunoscute:
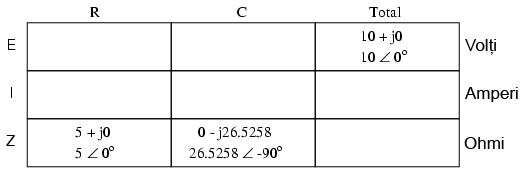
Fiind un circuit paralel, ştim faptul că tensiunea este aceeiaşi pe fiecare dintre coponente, prin urmare, putem introduce tensiunea totală (10 V∠ 0o) pe toate coloanele:

Acum putem aplica legea lui Ohm vertical (I=E/Z) pentru cele două coloane din tabel, calculând curentul prin rezistor, respectiv condensator:
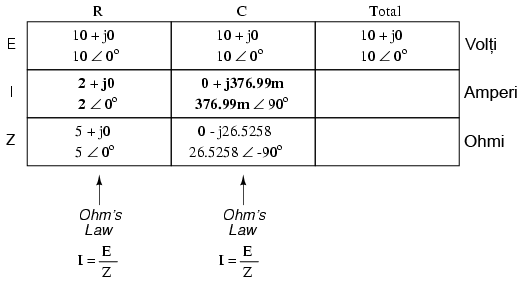
Asemenea circuitelor de curent continuu, curentul total este suma curenţilor de ramură (legea lui Kirchhoff pentru curent):
Formula de calcul a impedanţei totale
Impedanţa totală poate fi calculată folosind legea lui Ohm (Z=E/I), vertical, pe coloana „Total”. După cum am mai văzut, impedanţa paralelă poate fi calculată folosind o formulă echivalentă cu cea folosită pentru calcularea rezistenţei totale paralele. Trebuie amintit faptul că această regulă a impedanţei paralele se aplică indiferent de tipul impedanţelor ce le avem în paralel. Cu alte cuvinte, nu contează dacă avem circuite compuse exclusiv din rezistori paraleli, bobine paralele, condensatoare paralele sau orice alt tip de combinaţie între cele trei: sub forma impedanţei (Z), toţi termenii sunt comuni şi pot fi aplicaţi uniform în aceeiaşi formulă:
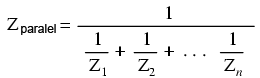
Singurul dezavantaj al acestei ecuaţii este volumul mare de muncă necesar pentru a efectua calculele matematice. Dar, indiferent de metoda ce o aplicăm pentru calcularea imedanţei paralel din circuitul de mai sus (fie folosind legea lui Ohm, fie formula echivalentă), rezultatul este identic: