< Curent alternativ
3 Reactanta inductiva
3.1 Circuite rezistive în curent alternativ
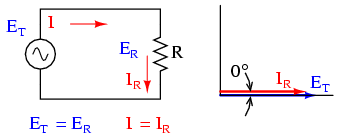
Să considerăm un circuit de curent alternativ pur rezistiv, caz în care tensiunea şi curentul sunt în fază (unghiul de defazaj dintre ele este 0o):
Dacă trecem curentul şi tensiunea din circuitul de mai sus pe un grafic, acesta va arăta aproximativ asfel:
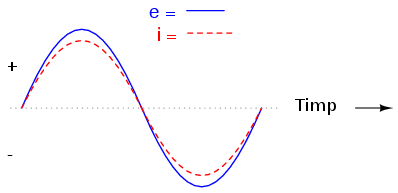
Deoarece rezistorul se opune pur şi simplu deplasării electronilor prin circuit în mod direct, în orice moment din timp, forma de undă a căderii de tensiune pe rezistor este exact în fază cu forma de undă a curentului prin acesta. Putem lua în considerare orice punct de pe axa orizontală a graficului şi compara valorile curentului şi ale tensiunii între ele (aceste puncte poartă denumirea de valori instantanee). Asfel, atunci când valoarea instantanee a curentului este zero, valoarea instantanee a tensiunii este şi ea zero. De asemenea, atunci când curentul prin rezistor atinge valoarea sa maximă pozitivă, tensiunea la bornele sale este şi ea la valoarea sa maximă pozitivă. În orice punct de-a lungul formelor de undă, putem aplica legea lui Ohm pentru valorile instantanee a curentului şi tensiunii.
Putem de asemenea să calculăm puterea disipată de rezistor şi să completăm graficul asfel:
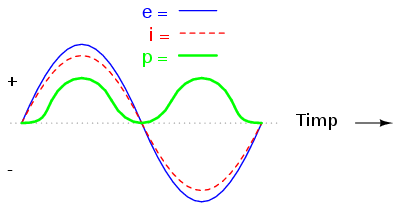
Se poate observa de pe grafic faptul că puterea nu are niciodată o valoarea negativă. Atunci când valoarea curentului este pozitivă, şi tensiunea este pozitivă, produsul celor două (p=ie) fiind prin urmare pozitiv. Atunci când curentul este negativ, şi tensiunea este negativă, ceea ce se traduce din nou printr-un produs pozitiv între cele două. Această polaritate unică ne spune de fapt că rezistorul disipă tot timpul putere ce este generată de sursă şi degajată de acesta sub formă de căldură. Indiferent de valoarea curentului, pozitivă sau negativă, un rezistor va disipa tot timpul energie.
3.2 Circuite inductive în curent alternativ
Bobinele au în schimb un comportament diferit faţă de cel al rezistorilor atunci când sunt introduse în circuit. Faţă de rezistor, care doar se opun treceri curentului prin acel punct din circuit în care aceştia sunt conectaţi (prin dezvoltarea unei căderi de tensiune direct proporţionale cu valoarea curentului), bobinele se opun variaţiei curentului prin ele, prin dezvoltarea unei căderi de tensiune direct proporţionale cu rata de variaţie a curentului. În conformitate cu legea lui Lenz, polaritatea aceastei tensiuni induse este asfel încât valoarea curentului să se menţină la valoarea curentă, şi anume, dacă valoarea curentului creşte , tensiunea indusă se va opune deplasării electronilor; în cazul descreşterii curentului, polaritatea este inversă pentru a putea împinge electronii şi a se opune descreşterii curentului. Această opoziţie la variaţia curentului poartă denumirea de reactanţă, în loc de rezistenţă.
Matematic, relaţia dintre căderea de tensiune pe o bobină şi rata variaţiei curentului prin aceasta, se exprimă asfel:
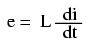
Expresia di/dt reprezintă derivata curentului cu timpul, adică rata de variaţia a curentului instantaneu (i) cu timpul, în amperi per secundă. „L” reprezintă inductanţă în Henry, iar „e” este tensiunea instantanee. Câteodată în loc de „e” se mai foloseşte şi „v”, dar cele două notaţii sunt echivalente.
Să analizăm un circuit pur inductiv simplu în curent alternativ. În acest, curentul este defazat în urmă faţă de tensiune cu 90o:
Graficul tensiunii şi al curentului în acest caz arată aproximativ asfel:
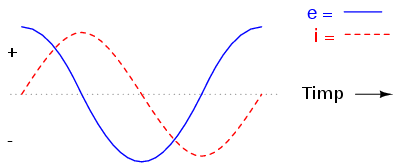
Reţineţi faptul că valoarea căderii de tensiune pe bobină este în funcţie de variaţia curentului prin aceasta. Prin urmare, tensiunea instantanee este zero ori de câte ori curentul instantaneu este la valoarea maximă, de vârf (pozitivă sau negativă), deoarece în acest caz variaţia, sau panta, este zero; tensiunea instantanee are o valoare maximă, de vârf, atunci când panta curentului instanteneu, sau variaţia acestuia este maximă (intersecţia formei de undă cu axa orizontală a timpului). Datorită acestui fapt, formele de undă sunt defazate cu 90o. Dacă ne uităm pe grafic, observăm că unda de tensiune are un mic „avantaj” faţa de una de curent; prin urmare, spunem că tensiunea este defazată cu 90o înaintea curentului, sau echivalent, curentul este defazat cu 90o în urma tensiunii.
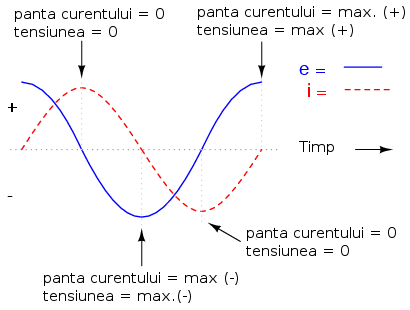
Lucrurile devin şi mai interesante atunci când introducem şi forma de undă a puterii pe grafic:
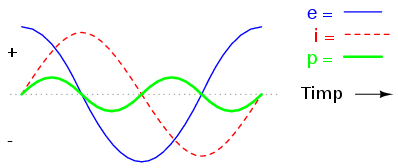
Deoarece puterea instantanee reprezintă produsul dintre tensiunea şi curentul instantaneu (p=ie), puterea este egală cu zero atunci când curentul sau tensiunea instantanee este zero. Ori de câte ori curentu şi tensiunea instantanee sunt ambele pozitive sau ambele negative, puterea este şi ea pozitivă. Dar, datorită faptului că cele două unde de tensiune, respectiv curent, sunt defazate între ele cu 90o, există momente în care una este pozitivă şi cealaltă negativă, rezultatul fiind o putere instantanee negativă:
Dar ce înseamnă putere negativă? Înseamnă că bobina generează putere înapoi în circuit, iar putere pozitivă înseamnă că aceasta absoarbe putere din circuit. Acest lucru dovedeşte faptul că bobina nu „consumă” putere precum o face un rezistor (ce o disipă sub formă de căldură), ci puterea absorbită din circuit este stocată sub formă de câmp magnetic. În cazul de faţă, datorită faptului că duratele de putere pozitivă şi negativă sunt perfect egale, bobină generează aceeiaşi cantitate de putere înapoi în circuit pe care absorbit-o într-o perioadă completă de timp. Practic, reactanţă (rezistenţă în curent continuu) bobine nu disipă energie, sau echivalent, energia disipată de aceasta este zero. Atenţie, cazul de sus este cel al unei bobine ideale, cu rezistenţă zero.
Opoziţia unei bobine faţă de variaţia curentului se traduce printr-o opoziţie faţă de curentul alternativ în general, curent ce este prin definiţie variabil în magnitudine instantanee şi direcţie (polaritate). Această opoziţie faţă de curent alternativ este similară rezistenţei, dar diferită prin faptul că rezultă întotdeaună într-o diferenţă de fază între curent şi tensiune, iar puterea disipată este zero. Datorită acestei diferenţe, are şi o denumire specificiă: reactanţă. Reactanţă în curent alternativ se exprimă în ohmi, la fel ca şi rezistenţa, doar că simbolul matematic este X, în loc de R. Pentru a fi mai exacţi, reactanţa asociata cu o bobină poartă numele de reactantă inductivă şi este simbolizată prin XL.
Din moment ce căderea de tensiune pe bobine este proporţională cu rata de variaţie a curentului, căderea de tensiune va fi mai mare pentru variaţii mai rapide de curent, şi mai mică pentru variaţii mai lente. Acest lucru înseamnă că reactanţă în ohmi pentru oricare bobină, este direct proporţională cu frecvenţă curentului alternativ. Matematic, acest lucru se exprimă asfel:
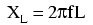
Dacă avem o bobină de 10 mH şi o conectăm într-un circuit cu frecvenţa variabilă, asfel: 60, 120 şi 2.500 Hz, reactanţa (inductivă) acesteia în fiecare dintre cele trei cazuri este următoarea:
| Frecvenţa (Hertz) | Reactanţă (Ohm) |
|---|---|
| 60 | 3.7699 |
| 120 | 7.5398 |
| 2500 | 157.0796 |
Viteza unghiulară a sistemului
În formula de calcul a reactanţei inductive, termenul „2πf” are un înţeles aparte. Este numărul de radiani pe secundă la care se „roteşte” curentul alternativ, dacă ne imaginăm că o perioadă a curentului alternativ reprezintă o rotaţie completă. Radianul este o unitate de măsură unghiulară: într-o rotaţie completă există 2π radiani, echivalentul a 360o într-un cerc complet. Dacă generatorul ce produce curentul alternativ are doi poli, va produce o rotaţie completă pentru fiecare rotaţie completă a arborelui, adică la fiecare 2π radiani, sau 360o. Dacă această constantă, 2π, este înmulţită cu frecvenţă în Herzi (număr de rotaţii pe secundă), rezultatul va reprezenta o valoare în radiani per secundă, valoare cunoscută sub numele de viteza unghiulară a sistemului de curent alternativ.
Viteza unghiulară poate fi reprezentată prin expresia 2πf, sau poate fi reprezentată folosind propriul său simbol, şi anume, litera grecească Omega, ω. Asfel, formula reactanţei, XL = 2πfL, poate fi rescrisă asfel: XL = ωL.
Trebuie înţeles faptul că această „viteză unghiulară” este o expresie a vitezei de rotaţie a formelor de undă în curent alternativ, o rotaţie completă fiind egală cu 2π radiani, şi nu este neapărat viteza actuală a arborelui generatorului ce produce curentul alternativ. Dacă generatorul este format din mai mult de doi poli, viteza unghiulară va fi multiplu de viteza arborelui. Din acest motiv, viteza unghiulară ω este câteodaţa exprimata sub formă de radiani electrici per secundă, pentru a face diferenţă între aceasta şi rotaţia mecanică.
Indiferent de modul în care reprezentăm viteza unghiulară a sistemului, este ştiut faptul că ractanţa bobinei este direct proporţională cu aceasta. Odată cu creşterea frecvenţei sistemului de curent alternativ (creşterea vitezei de rotaţie a arborelui generatorului), opoziţia bobinei faţă de curgerea curentului va fi tot mai mare, şi invers. Curentul alternativ într-un circuit inductiv simplu este egal cu raportul dintre tensiunea şi reactanţa inductivă, asemănător modului de calcul în curent continuu, sau în circuitele rezistive în curent alternativ; să considerăm un exemplu:
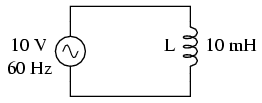
Totuşi, trebuie să fim atenţi la faptul că tensiunea şi curentul nu sunt în fază în acest caz. După cum am văzut, diferenţa de fază dintre cele două unde este de 90o. Dacă reprezentăm aceste unghiuri de fază matematic, sub forma numerelor complexe, observăm că opoziţia unei bobine faţă de curent posedă şi un unghi al fazei:


Matematic, spunem că unghiul de fază a opoziţiei bobinei faţă de curent este de 90o, ceea ce înseamnă o mărime imaginară pozitivă. Acest unghi de fază este foarte important în analiza circuitelor electrice, în special al celor complexe (în curent alternativ), unde există o interacţiune între rezistenţă şi reactanţă. Se va dovedi extrem de benefică reprezentarea opoziţiei faţă de curent a oricărei componente sub forma numerelor complexe şi nu sub forma cantităţilor scalare.
3.3 Circuite rezistiv-inductive serie. Impedanţa
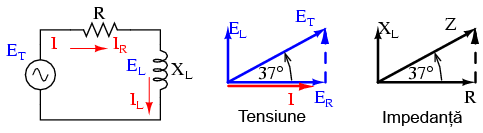
În secţiunile precedente, am văzut ce se întâmplă într-un circuit electric de curent alternativ simplu pur rezistiv, respectiv pur inductiv. Acum vom considera ambele componente legate în serie şi vom studia efectele lor. Luăm aşadar ca şi exemplu un curcuit rezistiv-inductiv, caz în care curentul este defazat în urma tensiunii cu un unghi cuprins între 0o şi 90o
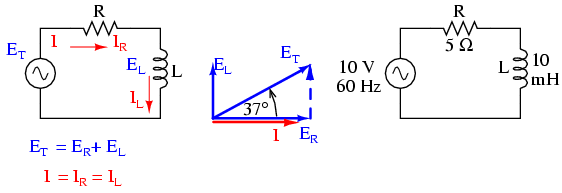
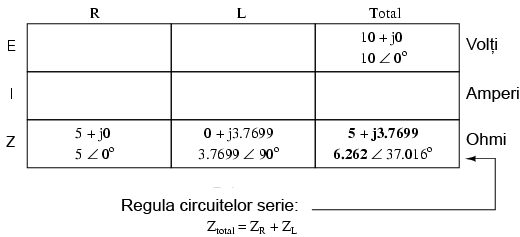
Rezistorul impune o rezistenţă de 5 Ω faţă de curent, indiferent de valoarea frecvenţei, iar bobina va oferi o reactanţă de 3.7699 Ω faţă de curentul alternativ la o valoare a frecvenţei de 60 Hz. Deoarece rezistenţa rezistorului este un număr real (5 Ω ∠ 0o, sau 5 + j0 Ω), iar reactanţa bobinei este un număr imaginar (3.7699 Ω ∠ 90o, sau 0 + j3.7699 Ω), efectul total (combinat) al celor două componente va crea o opoziţie faţă de curent egală cu suma complexă a celor două numere. Această opoziţie combinată va fi un vector. Pentru a putea exprima mai clar această opoziţie, avem nevoie de un nou termen pentru opoziţia faţă de curent pe lângă rezistenţă şi reactanţă. Acest termen poartă numele de impedanţă, iar simbolul lui este „Z”; unitatea de măsură este de asemenea ohm-ul, la fel ca şi a rezistenţei şi a reactanţei. În exemplul de mai sus, impedanţa totală a circuitului este:

Relaţia dintre impedanţă, curent şi tensiune este similară rezistenţei din legea lui Ohm:

De fapt, această expresie este o formă a legii lui Ohm mult mai cuprinzătoarea (mai generală) decât cea considerată în curent continuu (E=IR), la fel precum impedanţă este o expresie mult mai cuprinzătoare a opoziţiei faţă de deplasarea electronilor decât rezistenţa. Orice rezistenţă şi orice reactanţă, separate sau în combinaţii serie/paralel, pot fi şi trebuie exprimate ca şi o singură impedanţă într-un circuit de curent alternativ.
Pentru aflarea valorii curentului în circuitul de mai sus, trebuie mai întâi să impunem o referinţa pentru unghiul de fază a sursei de tensiune, iar în mod normal, aceasta se presupune a fi zero.
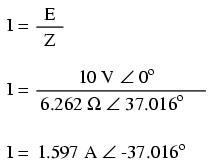
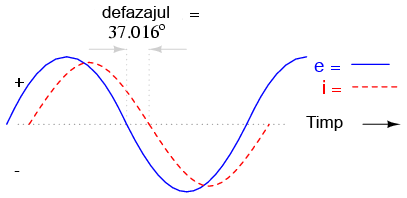
La fel ca şi în cazul circuitelor pur inductive, curentul este defazat în urma tensiunii (sursei), cu toată că de data aceasta defazajul nu este atât de mare, doar 37.016o, faţă de 90o în cazul circuitului pur inductiv.
Relaţiile de fază pentru rezistor şi bobină, luate individual, nu s-au modificat. Caderea de tensiune la bornele rezistorului şi curentul prin acesta sunt in fază (defazaj de 0o), iar defazajul dintre tensiune şi curent în cazul bobinei este de +90o. Putem verifica matematic acest lucru:

În formula de mai sus ZR semnifică impedanţa rezistivă, şi este acelaşi lucru cu rezistenţa. Tensiunea şi curentul prin rezistor sunt în fază, adică au acelaşi unghiu de fază.

Tensiunea la bornele bobinei are un unghiu de fază de 52.984o (faţă de unghiul de fază de referinţă, 0o), iar curentul prin bobina are un unghiu de fază de -37.016o, o diferenţă de exact 90o între cele două. Acest lucru ne spune că E şi I sunt defazate între ele tot cu 90o (doar în cazul bobinei).
Putem de asemenea să demonstrăm matematic că rezultatul sumei acestor valori complexe este tensiunea totală, aşa cum rezultă din aplicarea legii lui Kirchhoff:
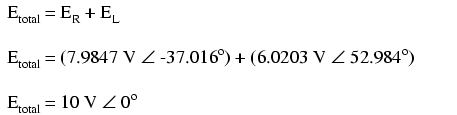
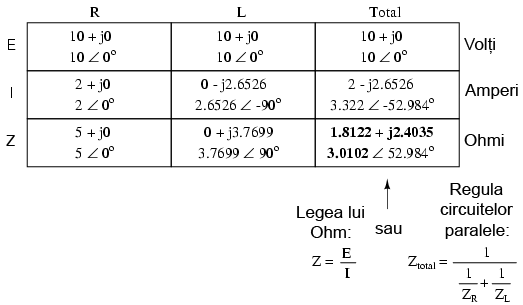
Aplicarea metodei tabelului
Cu toate aceste valori rezultate, chiar şi pentru un circuit simplu precum este acesta, este mai uşor să aplicăm metoda tabelului. Tabelul va conţine valorile pentru tensiune (E), curent (I) şi impedanţă (Z) pentru fiecare component în parte. Nu vom insera valorile propriu-zise ale rezistenţei şi inductanţei în ohm sau Henry, ci forma lor complexă:

Deşi nu este neapărat necesar, este folositor să trecem atât forma rectangulară (x + jy) cât şi pe cea polară (x ∠y) în fiecare tabel. Dacă folosim un calculator pentru a realiza automat aceste calcule complexe fără a mai fi nevoiţi să facem conversia între cele două forme, atunci această documentaţie suplimentară nu este deloc necesară. Totuşi, dacă suntem nevoiţi să efectuăm calculele „de mână”, atunci scrierea ambelor forme în tabel se va dovedi într-adevăr folositoare.
După ce am introdus în tabel toate datele cunoscute, putem trece la rezolvarea circuitului asemănător circuitelor de curent continuu: determinăm impedanţa totală din impedanţele individuale. Din moment ce acesta este un circuit serie, ştim că opoziţia faţă de curgerea electronilor (rezistenţă sau impedanţă) este aditivă, iar rezultatul îl reprezintă opoziţia totală:
Acum, după ce tensiunea şi impedanţa totală ne sunt cunoscute, putem aplica legea lui Ohm (I=E/Z) pentru determinarea curentului total din circuit:

La fel ca în cazul circuitelor de curent continuu, curentul total într-un circuit de curent alternativ serie este acelaşi prin oricare din componentele circuitului. Acest lucru este în continuare adevărat, deoarece într-un circuit serie există doar o singură cale pentru curgerea electronilor, prin urmare, rata lor de deplasare trebuie să fie uniformă în întreg circuitul. Prin urmare, putem trece valorile curentului total pentru fiecare component în parte (rezistor şi bobină) în tabel:
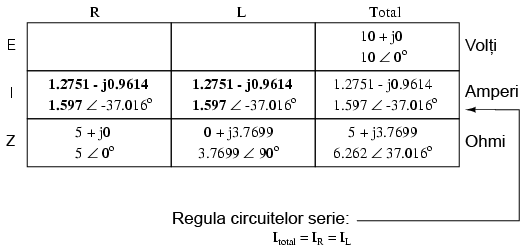
Acum, tot ceea ce mai avem de făcut este să completăm căderea de tensiune pe rezistor şi pe bobină. Aflarea acestor valori se realizează folosind legea lui Ohm (E=IZ), aplicată pe fiecare coloană a tabelului:
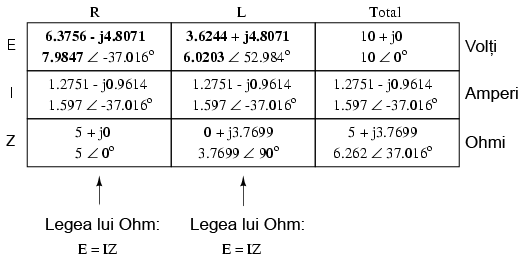
Tabelul este acum complet. De observat că am aplicat exact aceleaşi reguli ca şi în analiza circuitelor electrice în curent continuu, cu diferenţa ca toate valorile trebuie exprimate şi calculate sub formă complexă şi nu scalară precum era cazul în curent continuu. Atâta timp cât diferenţa de fază este reprezentată corect, nu există nicio diferenţă fundamentală între analiza unui circuit de curent alternativ faţă de unul în curent continuu.
Indicaţia instrumentelor de măsură
Să luăm acum în considerare relaţie dintre valorile calculate mai sus şi indicaţia tensiunii şi a curentului dată de instrumentele de măsură. Valorile din tabel care corespund cu valorile citite de pe un instrument de măsură sunt cele sub formă polară, nu rectangulară! Cu alte cuvinte, dacă am conecta un voltmetru la bornele rezistorului din circuit pentru aflarea căderii de tensiune, acesta va indica 7.9847 V (valoarea sub formă polară), nu 6.3756 V (valoarea reală sub formă rectangulară) şi nici 4.8071 V (valoarea imaginară sub formă rectangulară). Pentru a exprima acest lucru grafic, aparatele de măsură „indică” pur şi simplu lungimea vectorului (pentru tensiune sau curent). Notaţia rectangulară, deşi este mai uşor de folosit pentru operaţiile aritmetice de adunare şi scădere, este o formă de notaţia mai abstractă decât forma polară pentru măsurătorile reale. Dacă ar fi să folosim doar o singură notaţie, cea mai bună alegere ar fi cea polară, pentru că este singura ce are legătură directă cu măsurătorile reale.
Diagrama impedanţei
Impedanţa (Z) unui circuit serie R-L poate fi calculată cunoscând rezistenţă (R) şi reactanţa inductivă (XL). Din moment ce E=IR, E=IXL şi E=IZ, rezistenţa, reactanţa şi impedanţă sunt proporţionale cu tensiunea. Prin urmare, diagrama fazorială a tensiunii poate fi înlocuită cu o diagramă similară a impedanţei:
Exemplu
Găsiţi impedanţă totală a circuitului format dintr-un rezistor de 40 Ω conectat în serie cu o bobină de 79.59 mH, la o frecvenţă a sursei de alimentare de 60 Hz. Răspuns: Z = 40 + j30 = 50∠36.87o.
3.4 Circuite rezistiv-inductive paralel în curent alternativ
Să luăm în considerare aceleaşi componente din circuitul serie, dar să le conectăm de data aceasta în paralel:
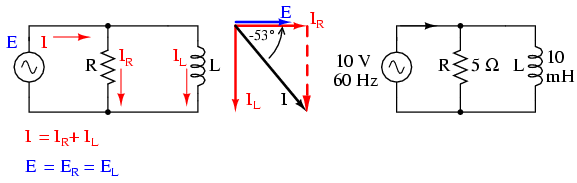
Deoarece sursa de tensiune are aceeiaşi frecvenţă ca şi în cazul circuitului serie, iar rezistorul şi bobina au aceleaşi valori ale rezistenţei şi inductanţei, acestea trebuie sa aibă aceleaşi valori ale impedanţei. Prin urmare, începem completarea tabelului cu aceleaşi valori date:

Singura diferenţă faţă de cazul precedent, este că de data aceasta vom aplica regulile circuitelor paralele, şi nu cele ale circuitelor serie. Metoda de lucru este practic aceeiaşi ca şi în cazul circuitelor de curent continuu. Cunoaştem faptul că tensiunea este aceeiaşi pe toate componentele într-un circuit paralel, aşa că putem copleta toate coloanele cu aceeiaşi valoare a tensiunii:
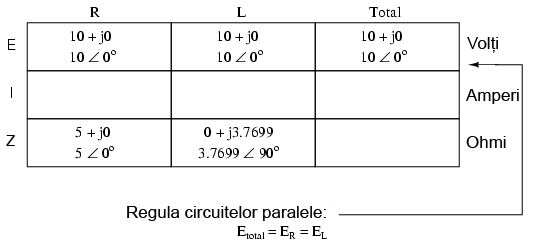
Acum putem aplica legea lui Ohm (I=E/Z) vertical pentru cele două coloane, calculând curentul prin rezistor şi curentul prin bobină:

La fel ca în cazul circuitelor de curent continuu, curenţii de ramură în circuitele de curent alternativ se însumează pentru a forma curentul total (legea lui Kirchhoff pentru curent este valabilă şi în acest caz):

Impedanţa totală poate fi calculată folosind legea lui Ohm (Z=E/I) vertical pe coloana „Total”. Impedanţa totală poate fi calculată, de asemenea, folosind o formulă echivalentă celei folosite pentru calcularea rezistenţei totale paralele:
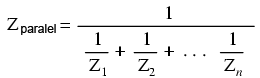
Indiferent ce motodă folosim, rezultatul este acelaşi: