< Curent alternativ

5 Reactanta RLC

5.1 R, X şi Z - recapitulare

Înainte de a începe să explorăm efectele rezistorilor, bobinelor şi a condensatoarelor conectate împreună în acelaşi circuit de curent alternativ, să recapitulăm mai întâi câteva noţiuni de bază.

Rezistenţa (R)

Rezistenţa este defapt frecarea întâmpinată de electroni, atunci când aceştia se află în mişcare. Toate materialele conductoare posedă o anumită rezistenţă (excepţie făcând supraconductoarele!), în special rezistorii. Atunci când curentul alternativ întâmpină o rezistenţă, căderea de tensiune produsă şi curentul prin aceasta sunt în fază. Simbolul matematic pentru rezistenţă este „R”, iar unitatea de măsură este Ohm-ul (Ω).

Reactanţa (X)

Reactanţa este defapt inerţia întâmpinată de electroni, atunci când aceştia se află în mişcare. Este prezentă peste tot unde există câmpuri electrice sau magnetice datorită tensiunii sau curentului aplicat, dar în special în condensatoare şi bobine. Atunci când curentul alternativ întâmpină o reactanţă, căderea de tensiune şi curentul prin aceasta sunt defazate cu 90^o. Simbolul matematic pentru reactanţă este „X”, iar unitatea de măsură este Ohm-ul (Ω).

Impedanţa (Z)

Impedanţa este o expresie completă a tuturor formelor de opoziţie întâmpinate de electroni, atunci când aceştia se află în mişcare, şi include efectele rezistenţei cât şi a reactanţei. Este prezentă în toate circuitele şi în toate componentele. Atunci când curentul alternativ întâmpină o impedanţă, căderea de tensiune şi curentul prin aceasta sunt defazate cu un unghi între 0^o şi 90^o. Simbolul matematic al impedanţei este „Z”, iar unitatea de măsură este Ohm-ul (Ω), sub formă complexă.

Componente ideale

Rezistorii perfecţi posedă doar rezistenţă, nu şi reactanţă. Bobinele şi condensatoarele perfecte posedă doar reactanţă, nu şi rezistenţă. Toate componentele posedă impedanţă, şi, datorită acestei proprietăţi universale a componentelor, este normal să exprimăm (traducem) valorile tuturor componentelor (rezistenţă, inductanţă şi capacitate) sub un termen comul, cel al impedanţei, ca prim pas în analiza oricărui circuit de curent alternativ:

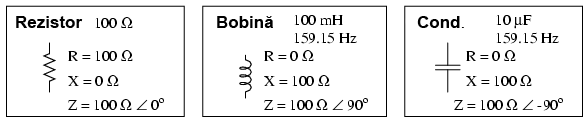
Unghiul de fază al impedanţei

Unghiul de fază al impedanţei pentru fiecare component este diferenţa de fază dintre căderea de tensiune la bornele acelui component şi curentul prin el. În cazul unui rezistor perfect, căderea de tensiune şi curentul sunt tot timpul în fază, prin urmare, unghiul de fază al impedanţei rezistorului (impedanţa rezistivă) este 0^o. Pentru o bobină perfectă, căderea de tensiune este tot timpul defazată înaintea curentului cu 90^o, prin urmare, unghiul de fază al impedanţei bobinei (impedanţa inductivă) este +90^o. Pentru un condensator perfect, căderea de tensiune este tot timpul defazată în urma curentului cu 90^o, prin urmare, unghiul de fază al impedanţei condensatorului (impedanţa capacitivă) este -90^o.

Legile lui Ohm şi Kirchhoff în curent alternativ

Impedanţele în curent alternativ se comportă analog rezistenţelor în curent continuu: se adună când sunt conectate în serie şi se micşorează în paralel. Legea lui Ohm pentru circuitele de curent alternativ, bazată pe impedanţă, nu pe rezistenţă, arată asfel:

Legile lui Kirchhoff, precum şi toate metodele de analiză a reţelelor şi toate teoremele valabile pentru curent continuu sunt valabile şi în curent alternativ, atâta timp când valorile sunt exprimate sub formă complexă şi nu scalară. Cu toate că această echivalenţă poate fi greu de aplicat aritmetic, conceptual, ea este simplă şi elegantă. Singura diferenţă reală între circuitele de curent continuu şi alternativ este cea legată de calcularea puterii. Doarece reactanţa nu disipă putere precum o face rezistenţă, conceptul de putere în circuitele de curent alternativ este radical diferit faţă de cele de curent alternativ.

5.2 Circuite RLC serie

Să considerăm următorul circuit RLC serie:

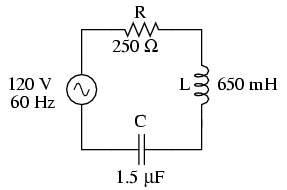
Primul pas este determinarea reactanţelor pentru bobină şi condensator:

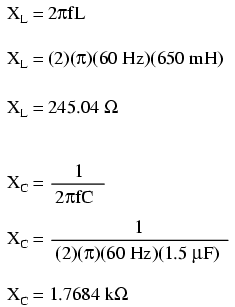
Următorul pas constă în exprimarea tuturor rezistenţelor şi reactanţelor într-o formă matematică comună: impedanţa. Ţineţi minte că reactanţă inductivă (a bobinei) se traduce printr-o impedanţă imaginară pozitivă(+90^o), iar reactanţă capacitivă (a condensatorului) se traduce printr-i impedanţă imaginară negativă (-90^o). Rezistenţa, desigur, este considerată o impedanţă „reală” pură (unghi polar de 0^o:

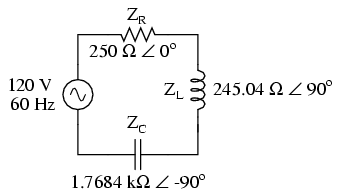
După ce toate valorile opoziţiei faţă de curent au fost exprimate sub forma comună a impedanţei, ca numere complexe, acestea pot fi manipulate la fel ca rezistenţele în curent continuu. Putem scrie toate valorile cunoscute într-un tabel, şi apoi să rezolvăm mai departe acest circuit:

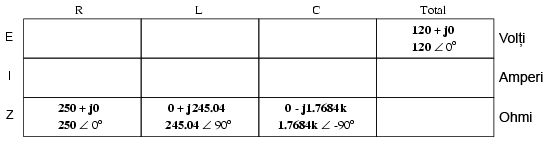
Circuitul de mai sus fiind unul serie, ştim că impedanţa totală este egală cu suma impedanţelor individuale:

Introducând valoarea impedanţei totale în tabel, obţinem:

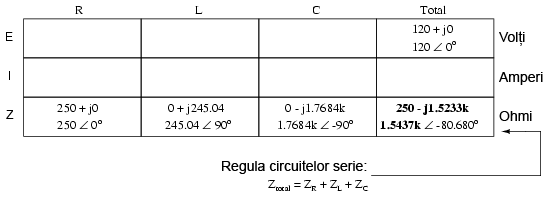
Putem acum să aplicăm legea lui Ohm (I=E/R), vertical, în coloana „Total” pentru a găsi curentul total din circuit:

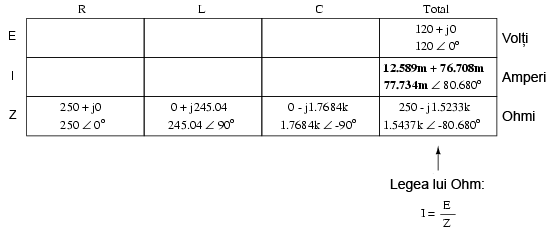
Fiind un circuit serie, curentul trebuie să fie acelaşi prin toate componentele:

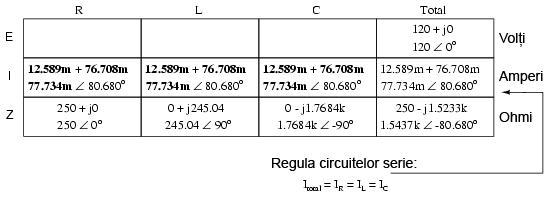
Putem aplica acum legea lui Ohm (E=IZ) fiecărui component în parte, pentru determinarea căderilor de tensiune:

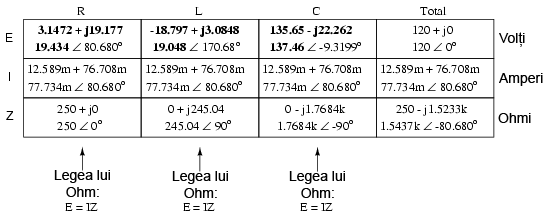
Putem observa ceva aparent ciudat în acest caz: cu toate că tensiunea sursei de alimentare este de doar 120 V, tensiunea la bornele condensatorului este de 137.46 V! De ce se întâmplă acest lucru? Răspunsul se află în interacţiunea dintre reactanţele inductive şi capacitive. Exprimată ca şi impedanţă, putem vedea că bobina se opune trecerii curentului într-un mod exact invers faţa de condensator. Exprimată sub formă rectangulară, impedanţă bobinei posedă un termen imaginar pozitiv, iar condensatorul un termen imaginar negativ. Când aceste două impedanţe contrare sunt adunate (în serie), ele tind să se anuleze reciproc! Cu toate că ele se adună, suma lor este defapt mai mică decât oricare dintre impedanţe (inductive sau capacitive) considerate separat. Acest lucru este analog sumei dintre un scalar pozitiv şi unul negativ.

Dacă impedanţa totală într-un circuit serie ce conţine atât elemente inductive cât şi capacitive, pe lângă cele rezistive (RLC), este mai mică decât impedanţa individuală a oricărui element luat separat, atunci curentul total din circuit trebuie să fie mai mare decât curentul rezultat în cazul în care doar componeta capacitivă sau inductivă ar fi introduse în circuit. Odată cu apariţia acestui curent prin fiecare element, mai mare decât în mod normal, pot apărea căderi de tensiune mai mari decât tensiunea sursei de alimentare, pe anumite elemente din circuit!

5.3 Circuite RLC paralel

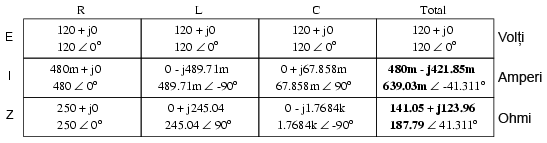
Putem folosi aceleaşi componente de la circuitul serie, dar conectate în paralel de această dată:

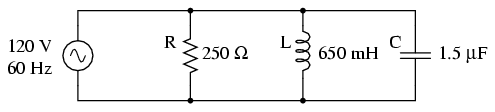
Faptul că aceste componente sunt conectate în paralel şi nu în serie, nu are absolut niciun efect asupra impedanţelor individuale. Atâta timp cât frecvenţa sursei de tensiune este aceeiaşi, reactanţele inductive şi capacitive nu se vor modifica deloc:

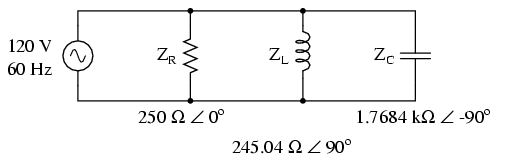
După ce am exprimat valorile tuturor componentelor ca şi impedanţe (Z), putem începe analiza circuitului prin completarea tabelului, folosind regulile circuitelor serie de data aceasta:

Ştiind că într-un circuit paralel, căderea de tensiune este aceeiaşi pe toate componentele, putem trece valoarea tensiunii totale în fiecare coloană:

Acum putem aplica legea lui Ohm (I=E/Z) vertical, pe fiecare coloană, pentru determinarea curentului prin fiecare component:

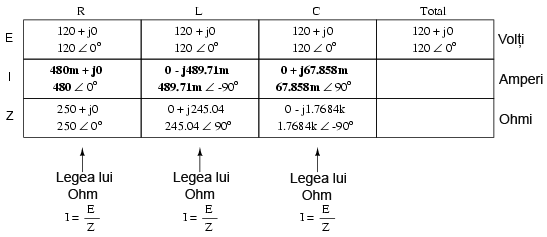
Există două strategii pentru calcularea curentului şi a impedanţei totale. Prima presupune calcularea impedanţei totale din impedanţele individuale conectate în paralel folosind formula echivalentă (Z_Total = 1/(1/Z_R + 1/Z_L + 1/Z_C), iar curentul total ca raport dintre tensiunea sursei de alimentare şi impedanţa totală (I=E/Z). Totuşi, rezolvarea ecuaţiei presupune un calcul dificil cu numere complexe. A doua metodă de calcul presupune aflarea curentului total ca sumă a curenţilor de ramură, iar apoi, folosind legea lui Ohm, putem determina impedanţa totală ca raport dintre tensiunea sursei de alimentare şi curentul total (Z=E/I). Rezultatul final trebuie să fie acelaşi în ambele cazuri.

5.4 Circuite RLC serie-paralel

Să luăm ca şi exemplu următorul circuit serie-paralel:

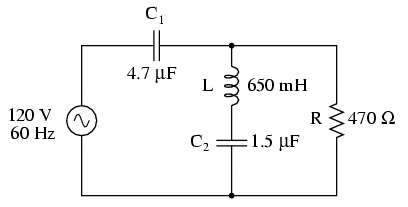
Primul pas este determinarea valorilor impedanţelor (Z) pentru toate componentele, în funcţie de frecvenţa sursei de alimentare. Pentru a realiza acest lucru, trebuie mai întâi să determinăm valorile reactanţelor (X) bobinelor şi condensatoarelor iar apoi să exprimă reactanţele (X) şi rezistenţele (R) sub formă de impedanţe (Z):

Putem acum să completăm valorile iniţiale în tabel:

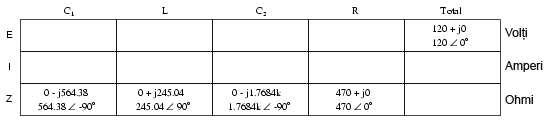
Întrucât avea de a face în acest caz cu un circuit serie-paralel combinat, nu putem afla impedanţa totală dintr-un singur pas. Prima dată luăm L şi C₂ ca şi combinaţie serie; impedanţa combinată va fi suma impedanţelor individuale. Apoi, impendaţa rezultată o vom combina în paralel cu impedanţa rezistorului, rezultatul fiind o nouă impedanţă. Şi, în sfârşi, impedanţa precedentă o combinăm în serie cu impedanţa C₁ şi ajungem la valoarea impedanţei totale a circuitului considerat.

Pentru a putea reprezenta toţi aceşti paşi sub format tabelar, va trebui să mai adăugam câteva coloane (folosim de fapt un al doilea tabel din motive de spaţiu), fiecare coloană reprezentând combinaţia respectivă.

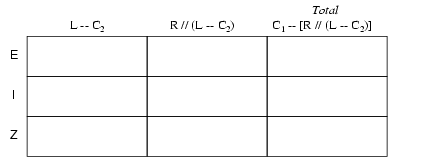
Calcului acestor impedanţe combinate necesită sume complexe pentru combinaţiile serie şi utilizarea formulei echivalente pentru impedanţele paralel.

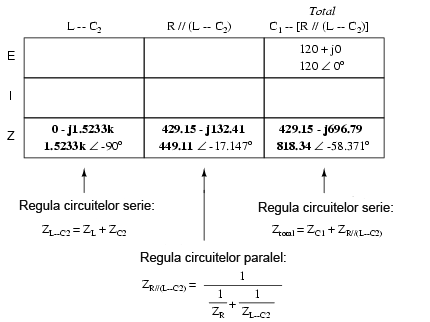
Putem să renunţăm la coloana total din primul tabel, întrucât aceasta apare în cel de al doilea tabel.

Acum că ştim impedanţa şi tensiunea totală, putem aplica legea lui Ohm, vertical, pe coloana „Total” pentru calcularea curentului total:

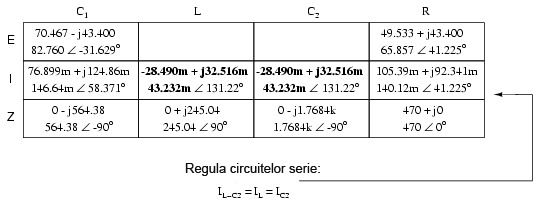
În acest moment, putem căuta componente sau combinaţii de componente ce au fie aceeiaşi cădere de tensiune sau acelaşi curent. Iar în acest caz, atât prin C₁ cât şi prin combinaţia paralel R//(L–C₂) trece acelaşi curent, întrucât ele sunt în serie. Putem trece prin urmare aceste valori în ambele coloane:

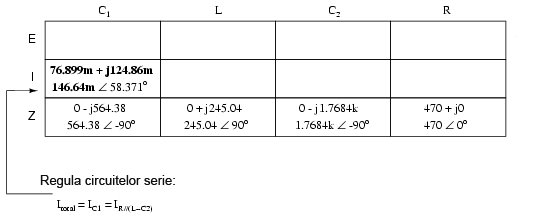
Acum putem calcula căderile de tensiune pe C₁ şi pe combinaţia serie-paralel R//(L–C₂ folosind legea lui Ohm (E=IZ), vertical:

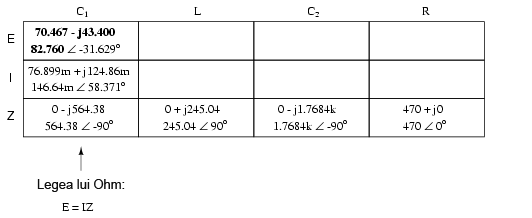
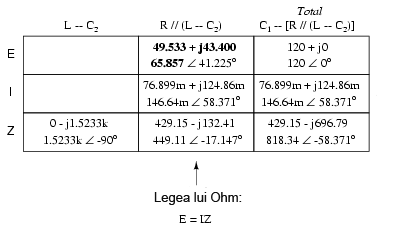
Din nou, putem căuta componente ce au aceeiaşi cădere de tensiune sau curent. În acest caz, rezistorul (R) şi combinaţia serie a bobinei cu cel de al doilea condensator (L–C) au aceeiaşi cădere de tensiune, pentru că cele două seturi de impedanţe sunt conectate în paralel. Asfel, putem trece valorile tensiunii calculate mai sus în coloanele R şi L–C₂:

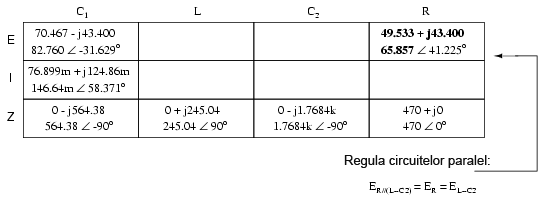
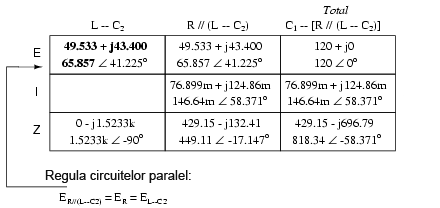
Următorul pas este calcularea curentului prin rezistor şi prin combinaţia serie L–C₂. Tot ceea ce trebuie să facem este să aplicăm legea lui Ohm (I=E/Z), vertical, în ambele coloane:

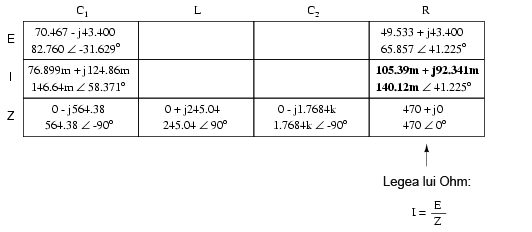
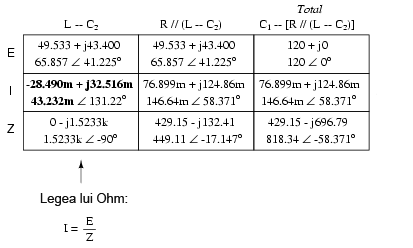
Din moment ce L şi C₂ sunt conectate în serie şi cunoaştem curentul prin combinaţie serie a impedanţei, putem trece aceeleaşi valori şi în coloanele L şi C₂, folosind regula conform căreia în circuitele serie, curentul prin fiecare component este acelaşi:

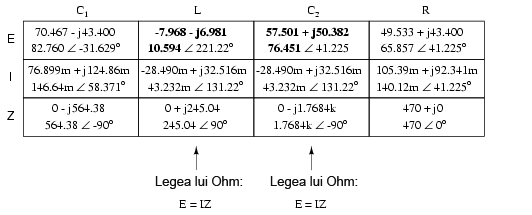
Ultimul pas constă în aplicarea legii lui Ohm (E=IZ), vertical, pentru calcularea căderilor de tensiune pentru cele două coloane rămase (L şi C₂):

5.5 Susceptanţa şi admitanţa

În studiul circuitelor electrice de curent continuu am întâlnit termenul de conductanţă; aceasta se defineşte ca inversul rezistenţei. Matematic, aceasta reprezintă reciproca rezistenţei, 1/R, termen ce în formula rezistenţei paralele este chiar conductanţa.

Pe când „rezistenţa” denotă cantitatea opoziţiei faţă de deplasarea electronilor, „conductanţa” reprezintă uşurinţa de deplasare a electronilor. Unitatea de măsură pentru conductanţă este Siemens, iar simbolul matematic, „G”.

Componentele reactive, precum bobinele şi condensatoarele, se opun trecerii curentului (deplasării electronilor) în funcţie de timp şi nu într-un mod constant, uniform, ca în cazul rezistorilor. Această opoziţie în funcţie de timp se numeşte reactanţă, notată cu „X” şi măsurată de asemenea în Ohm.

La fel cum pentru rezistenţă există o mărime complementară, conductanţa, şi pentru expresia reactanţei există o mărime complementară, denumită susceptanţă. Matematic, susceptanţă este inversa (reciproca) reactanţei, 1/X. Simbolul matematic este „B”, iar unitatea de măsură este tot Siemens.

În aceeiaşi ordine de idei, există şi o mărime complementară pentru impedanţă, admitanţă. Matematic, aceasta este inversa impedanţei, 1/Z. Simbolul matematic este „Y”, iar unitatea de măsură este Siemens. La fel ca şi impedanţa, admitanţa este o cantitate complexă, nu scalară.

Chiar dacă în calculele uzuale nu vom întâlni prea des aceşti termeni, este bine de ştiut că aceştia există. p>