< Curent alternativ

6 Rezonanta

6.1 Pendulul electric

Condensatoarele stochează energie sub formă de câmp electric, iar această energie stocată se manifestă electric sub formă de potenţial: tensiune statică. Bobinele stochează energie sub formă de câmp magnetic, iar această energie stocată se manifestă electric sub formă cinetică: curent. Ambele elemente sunt însă feţele opuse ale aceleiaşi monede; ambele sunt elemente reactive ce stochează şi eliberează energie în două moduri complementare. Când aceste două tipuri de componente reactive sunt conectate împreună, rezultatul modului lor complementar de stocare a energiei este unul neobişnuit.

Dacă unul dintre cele două componente, fie condensatorul, fie bobina, este iniţial încărcat, cele două componente vor schimba energie între ele, de la unul la altul, creând propria lor tensiune şi curent alternativ. Dacă presupunem că ambele componente sunt supuse unei tensiuni aplicate brusc (de la o baterie, de exemplu), condensatorul se va încărca foarte repede, iar bobina se va opune variaţiei curentului; prin urmare condensatorul va fi încărcat, iar bobina descărcată:

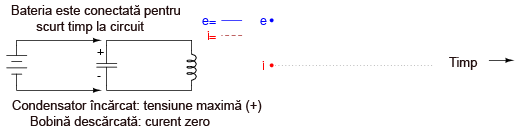
Condensatorul va începe să-şi descarce energia înmagazinată pe bobină, prin urmare, tensiunea va descreşte. Între timp, bobina va conduce curent electric şi va înmagazina energie sub formă de câmp magnetic; rezultatul este creşterea curentului în circuit:

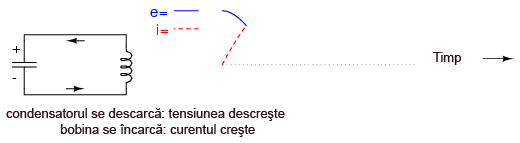
Bobina va continua să se încarce şi să menţină curgerea electronilor în circuit până când condensatorul va fi complet descărcat (tensiune zero la bornele sale):

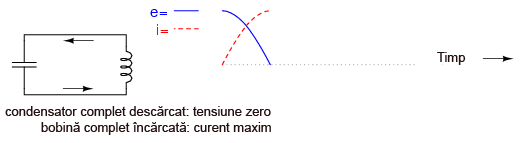
Bobina va menţine curentul chiar şi fără existenţa unei tensiuni aplicate la bornele sale; de fapt, va genera o tensiune (precum o baterie) pentru menţinerea direcţiei curentului. Condensatorul, fiind elementul ce primeşte acest curent, va începe să acumuleze o sarcină de polaritate inversă faţă de polaritatea sa iniţială:

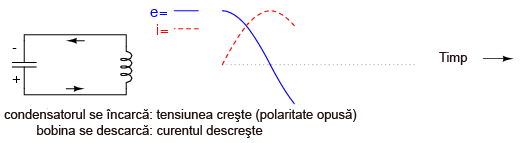
Atunci când curentul prin bobină se epuizează iar energia înmagazinată ajunge la zero, tensiunea condensatorului va fi maximă, şi de polaritate opusă tensiunii iniţiale:

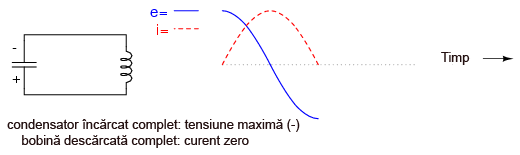
Am ajuns acum la o situaţie foarte similară celei iniţiale: condensatorul este complet încărcat iar curentul prin circuit este zero (bobină descărcată). Condensatorul va începe (din nou) să se descarce prin/pe bobină, ducând la creşterea curentului (în direcţie opusă faţă de cazul iniţial) şi descreşterea tensiunii pe măsură ce energia înmagazinată de condensator tinde spre zero:

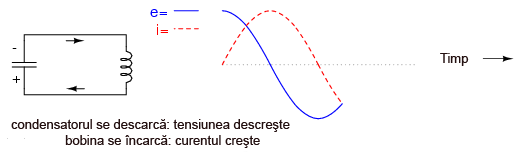
Într-un final, condensatorul se va descărca complet (zero volţi), iar bobina va deveni încărcată complet (curent maxim):

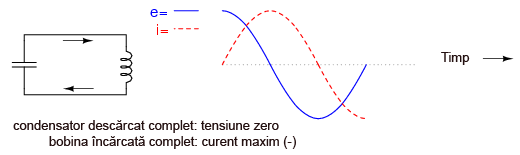
Bobina, încercând să menţină direcţia curentului, se va comporta din nou precum o sursă, generând tensiune electrică precum o baterie pentru menţinerea acestuia. În acest fel, condensatorul va începe să se încarce din nou, iar amplitudinea curentului din circuit va descreşte din nou:

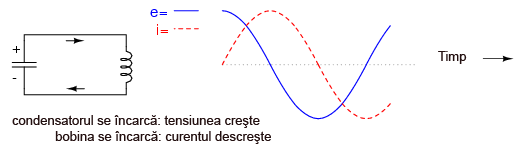
Până la urmă condensatorul se va încărca complet (din nou) pe măsură ce energia bobinei se apropie de zero. Tensiunea se va afla din nou la valoarea maximă pozitivă, iar curentul la zero. Acest ultim pas duce la completarea unei perioade pe parcursul cărei cele două componente au schimbat între ele aceeiaşi energie electrică:

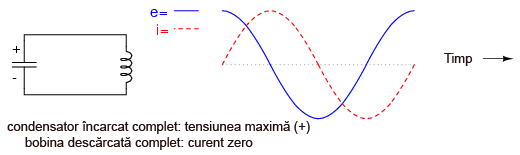
Această oscilaţie a energie de la un component la altul va continua cu o amplitudine a semnalelor din ce în ce mai mică, descreştere datorată pierderilor de putere cauzate de rezistenţele parazite din circuit, până când întregul proces se opreşte cu totul. În mare, acest comportament este asemănător comportamentului pendulului: pe măsură ce masa pendului oscilează înainte şi înapoi, există o transformare continuă între energia cinetică (mişcare) şi energia potenţială (înălţime), asemănător circuitului format din bobină şi condensator.

În punctul în care înălţimea pendulului este maximă, masa acestuia se opreşte pentru o scurtă perioadă de timp, urmată de schimbarea direcţiei sale de mişcare. În acest punct, energia potenţială (înălţime) este maximă iar energia cinetică (mişcare) este zero. Pe măsură ce masa oscilează înapoi, trece rapid printr-un punct în care coarda este direcţionată perpendicular pe direcţia pământului. În acest punct, energia potenţială (înălţime) este zero iar energia cinetică (mişcare) este la valoarea sa maximă. Precum un circuit, oscilaţia înainte şi înapoi a pendului va continua cu o amplitudine a oscilaţiilor din ce în ce mai mică, descreştera datorată frecării cu aerul (rezistenţă) ce disipă energie. Tot precum în cazul circuitului de mai sus, poziţia şi viteza pendulului trasate pe un grafic (timp-amplitudine) trasează două unde sinusoidale defazate între ele cu 90^o.

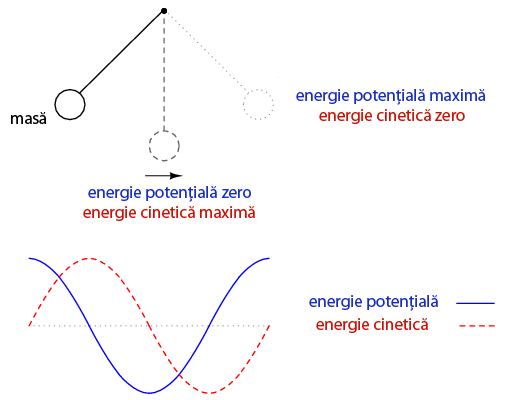
În fizică, această oscilaţie sinusoidală naturală este cunoscută sub numele de mişcare armonică simplă. Aceleaşi principii stau însă şi la baza circuitelor formate din condensator şi bobină, de genul celui văzut mai sus. O proprietate interesantă al oricărui tip de pendul, este că perdioada sa depinde de lungimea braţului şi nu de greutatea masei de la capătul acesteia. De aceea pendulul va continua să oscileze la aceeiaşi frecvenţă pe măsură ce amplitudinea oscilaţiilor scade. Rata oscilaţiilor este independentă de cantitatea de energie stocată în pendul.

Acelaşi lucru este valabil şi pentru circuitul bobină/condensator. Rata oscilaţiilor este stric dependentă de mărimea condensatorului şi a bobinei, şi nu de cantitatea de tensiune (sau curent) disponibilă în circuit. Proprietatea sa de a menţine o singură frecvenţă, naturală, indiferent de valoarea energiei stocate, este de o mare importanţă în realizarea circuitelor electric.

Totuşi, această tendinţă de oscilaţie, sau rezonanţă, la o anumită frecvenţă, nu este limitată doar la circuitele concepute special în acest scop. De fapt, aproape orice circuit de curent alternativ ce conţine o combinaţie de capacităţi şi inductivităţi (circuit „LC”) tinde să manifeste efecte neobişnuite atunci când frecvenţa sursei de alimentare în curent alternativ se apropie de frecvenţa naturală. Acest lucru este valabil indiferent de scopul pentru care circuitul a fost creat.

Dacă frecvenţa sursei de alimentare a circuitului este exact frecvenţă naturală de oscilaţie a combinaţiei LC, spunem că circuitul se află într-o stare de rezonanţă. Efectele neobişnuite vor atinge un maxim în această condiţie de rezonanţă. Din acest motiv, trebuie să calculăm din timp frecvenţa de rezonanţă pentru diferite combinaţii de L şi C, şi să ţinem cont de efectele acesteia asupra circuitului.

6.2 Rezonanţa paralel

Putem ajunge la o stare de rezonanţă într-un circuit oscilator (LC), dacă reactanţele condensatorului şi a bobinei sunt egale între ele. Deoarece reactanţa inductivă creşte odată cu creşterea frecvenţei, iar reactanţa capacitivă scade cu creşterea frecvenţei, există doar o singură frecvenţă unde cele două reactanţe vor fi egale.

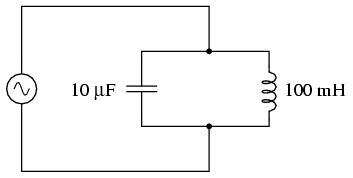
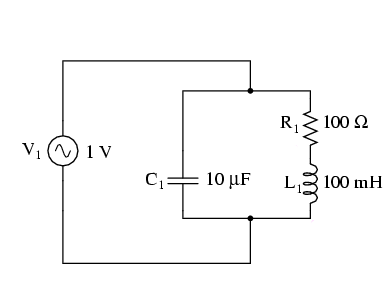
În circuitul de mai sus, avem un condensator de 10 µF şi o bobină de 100 mH. Din moment ce cunoaştem ecuaţiile pentru determinarea reactanţelor, oricare ar fi valoarea frecvenţei, iar ceea ce ne interesează este punctul în care cele două reactanţe sunt egale între ele, putem rezolva ecuaţia formată din egalitatea celor două reactanţa pentru a afla frecvenţa de rezonanţă (naturală):

Aceasta este formula prin care putem afla frecvenţa de rezonanţă a unui circuit oscilator, atunci când cunoaştem valorile inductanţei (L) şi a capacităţii (C). După introducerea valorilor L şi C în formula de mai sus, ajungel la frecvenţă de rezonanţă de 159.155 Hz.

Ceea ce se întâmplă la rezonanţă este interesant. Fiindcă reactanţa inductivă este egală cu cea capacitivă, impedanţa totală creşte spre infinit, ceea ce înseamnă că circuitul oscilator nu „consumă” deloc curent de la sursa de tensiune! Putem calcula impedanţele individuale ale condensatorului de 10 µF şi a bobinei de 100 mH, ca mai apoi să aplicăm formula impedanţei paralele pentru a demonstra matematic ceea ce am spus mai sus:

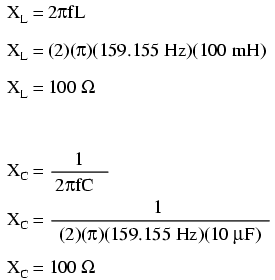
Prin urmare, ambele impedanţe sunt egale, 100 Ω. Putem acum să folosm formula impedanţei paralel:

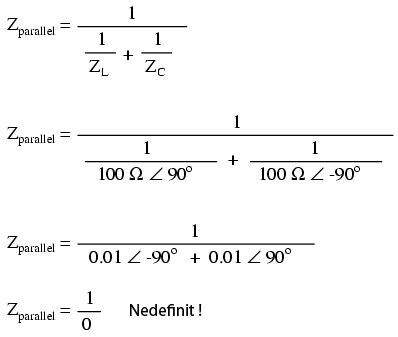
Desigur, nu putem face raportul unui număr cu zero pentru a ajunge la un rezultat care să aibă sens, dar putem spune că rezultatul tinde spre infinit pe măsură ce valorile celor două impedanţe paralele se apropie una de cealaltă. Practic, acest lucru înseamnă că impedanţa totală a circuitului oscilator la rezonanţă este infinită (se comportă precum un circuit deschis).

Grafic, amplitudinea curentului din circuit în funcţie de frecvenţa sursei de alimentare arată asfel:

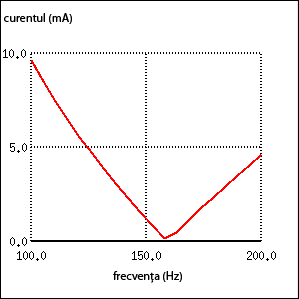
Punctul de pe grafic unde curentul este zero, coincide cu frecvenţa de rezonanţă calculată mai sus, 159.155 Hz.

6.3 Rezonanţa serie

Un efect similar rezonanţie parale are loc şi în circuitele inductiv/capacitive serie. Atunci când este atinsă o stare de rezonanţă (reactanţa capacitivă este egală cu cea inductivă), cele două impedanţe se anulează reciproc iar impedanţa totală scade la zero!

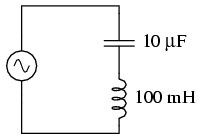
Fiindcă impedanţa serie totală este 0 Ω la frecvenţa de rezonanţă de 159.155 Hz, se va produce un scurt circuit la bornele sursei de curent alternativ la rezonanţă. Graficul curentului în funcţie de frecvenţă arată asfel:

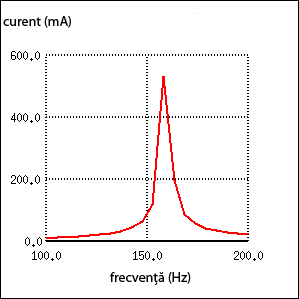
Putem observa de pe grafic, că la frecvenţa de rezonanţă de 159.155 (aproximativ), valoarea curentului prin circuit este maximă, ceea ce sugerează un scurt-circuit. Formula frecvenţei de rezonanţă calculată anterior este valabilă atât pentru circuitele LC paralel cât şi pentru cele serie:

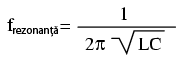
Atenţie, datorită curenţilor mari ce se pot dezvoltă într-un circuit LC serie la rezonantă, este posibilă apariţia unor căderi de tensiune periculoase pe condensator şi bobină, întrucât fiecare component are o impedanţă suficient de mare. Dacă alimentăm acest circuit cu doar 1 V, căderile de tensiune pe cele două componente pot atinge valori impresionante de aproximativ 70 V ! Prin urmare, fiţi foarte atenţi atunci când experimentaţi cu asfel de circuite!

6.4 Aplicaţii ale rezonanţei

Până acum, fenomenul rezonanţei pare doar o curiozitate nefolositoare, sau chiar dăunătoare,mai ales în cazul scurt-circuitării sursei de tensiune alternativă în circuitul serie. Totuşi, rezonanţa este o proprietate valoroasă a circuitelor de curent alternativ, fiind folosită într-o varietate de aplicaţii.

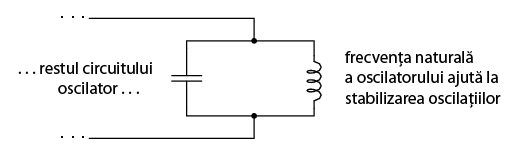
Una dintre aplicaţiile rezonanţei constă în atingerea unei frecvenţe stabile în circuitele folosite pentru producerea semnalelor alternative. De obicei este folosit un circuit paralel în acest scop, condensatorul şi bobina fiind conectate împreună, schimbând energie între ele, alternativ. La fel cum pendulul poate fi folosit pentru stabilizarea frecvenţei oscilaţiilor ceasurilor, un circuit oscilator (paralel) poate fi folosit pentru stabilizarea frecvenţei electrice a unui circuit oscilator de curent alternativ. După cum am mai spus, frecvenţa impusă de circuitul oscilator depinde doar de valorile L şi C, şi nu de amplitudinea tensiunii sau a curentului din circuit.

O altă aplicaţie a rezonanţei este în circuitele în care efectele impedanţelor mărite sau micşorate, la o anumită frecvenţă, sunt de dorit. Un circuit rezonant poate fi folosit pentru „blocarea” (impedanţă mare) unei anumite frecvenţe sau a unui domeniu de frecvenţe; circuitul se comportă în acest caz precum un „filtru”, pentru selectarea anumitor frecvenţe în defavoarea altora. Aceste circuite sunt de fapt denumite filtre, iar studiul lor constituie o întreagă disciplină.

În principiu, acesta este şi modul de funcţionare al unui aparat de radiorecepţie, ce selectează o anumită frecvenţă (post radio) din seria frecvenţelor variate recepţionate de antenă.

6.5 Rezonanţa serie-paralel. Antirezonanţa

În circuitele reactive simple fără rezistenţă (sau rezistenţă foarte mică), efectele impedanţelor la frecvenţa de rezonanţă vor fi cele prezise de ecuaţia acesteia. Într-un circuit LC serie, aceasta înseamnă impedanţă infinită. În circuitele LC serie, înseamnă impedanţă zero (la rezonanţă).

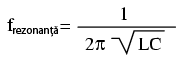
Totuşi, dacă începem să introducem rezistenţă în circuitele LC, această formulă de calcul pentru rezonanţă nu mai este utilizabilă. Vom luat câteva circuite LC ca şi exemplu, folosind aceleaşi valori pentru capacitate şi inductanţă ca şi înainte: 10 µF şi 100 mH. Frecvenţa de rezonanţă, potrivit formulei, ar trebui să fie 159.155 Hz, dar să vedem ce se întâmplă atunci când introducem un rezistor în circuit:

Circuit LC paralel; rezistor în serie cu bobina

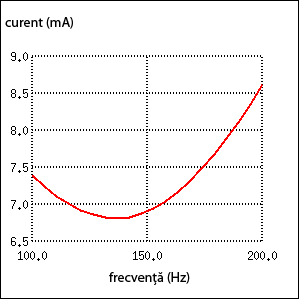
Rezistorul conectat în paralel cu bobina produce un curent minim, ce nu este zero, la frecvenţa de 136.8 Hz, şi nu la 159.2 Hz, valoarea calculată.

Circuit LC paralel; condensatorul în serie cu rezistorul

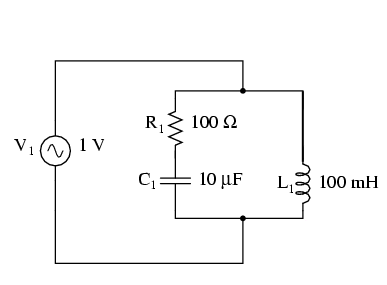
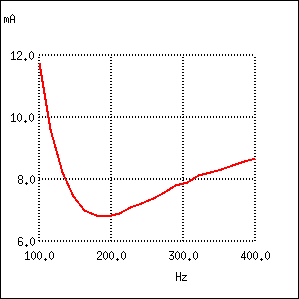
Curentul minim în acest caz este la frecvenţa de 180 Hz, nu la 159.2.

Circuit LC serie; rezistor paralel cu bobina

Întorcându-ne la circuitul LC serie, vom conecta o rezistenţă în paralel cu bobina. În circuitul de mai jos, rezistorul R₁ de 1 Ω este conectat în serie cu bobina şi condensatorul pentru limitarea curentului total prin circuit la rezonanţă. Rezistorul „extra” pe care îl introducem în circuit pentru influenţarea frecvenţei de rezonanţă este rezistorul R₂ de 100 Ω:

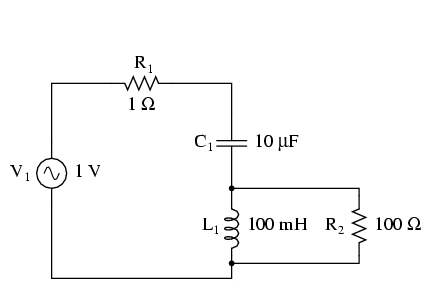
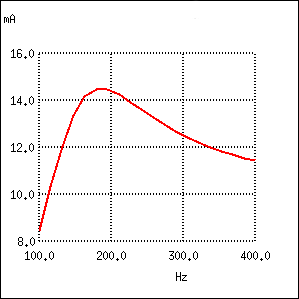
Circuitul rezonant serie (LC) cu un rezistor conectat în paralel cu bobina, prezintă un curent maxim la o frecvenţă de 180 Hz, faţă de 159.2.

Circuit LC serie; rezistor paralel cu condensatorul

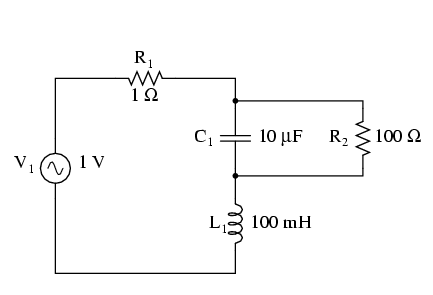
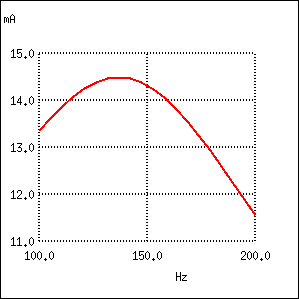
Şi în acest caz, curentul maxim prin circuit nu se mai produce la frecvenţa de 159.2 Hz, ci la 136.8 Hz.

Antirezonanţa

Tendinţa rezistenţei de modificare a punctului în care impedanţa atinge maximul sau minimul într-un circuit LC, poartă numel de antirezonanţă.

Din nou, efectele de mai sus ilustrează natura complementară a condensatoarelor şi a bobinelor: rezistenţa serie cu unul dintre ele crează un efect de antirezonanţă echivalent cu rezistenţa paralel cu celălalt. Dacă ne uităm şi mai atent la graficele de mai sus, putem observa că frecvenţele de rezonanţă sunt modificate cu aceeiaşi valoare, iar forma graficelor complementare sunt în oglindă!

Nu este foarte greu să adăugăm o rezistenţă într-un circuit LC, dar, deşi confecţionarea condensatorilor cu rezistenţe neglijabile, este posibilă, bobinele suferă la acest capitol; rezistenţele lor sunt mari datorită lungimilor conductorilor folosiţi la confecţionarea acestora. Mai mult decât atât, rezistenţa conductorilor tinde să crească odată cu creşterea frecvenţei de funcţionare, datorită efectului pelicular, efect ce se manifestă prin excluderea deplasării curentului alternativ prin centrul conductorului, reducând prin urmare secţiunea transversală a firului şi mărind asfel rezistenţa sa. Asfel, bobinele nu doar că au rezistenţă, dar au o rezistenţă variabilă, dependentă de frecvenţă.

Pe lângă asta, bobinele se mai confruntă şi cu pierderi, datorită miezurilor de fier folosite, efect cunoscut sub numele de curenţi turbionari.

Circuit RLC serie

O excepţie de la regula conform cărei o rezistenţă adiţională într-un circuit LC modifică valoarea rezistenţei de rezonanţă, este circuitul RLC serie. Atâta timp cât toate componentele sunt conectate în serie, frecvenţa de rezonanţă nu va fi afectată de rezistenţa în plus introdusă în circuit. Graficul variaţiei curentului în funcţie de frecvenţă este prezentat mai jos:

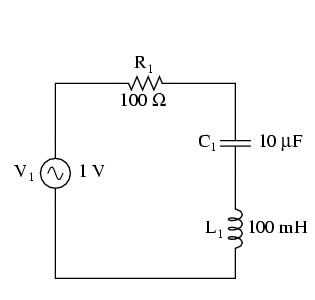
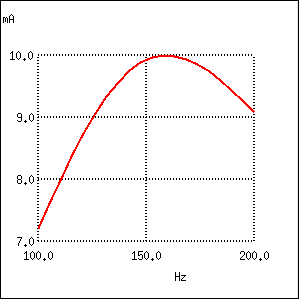
Valoarea curentului maxim este din nou atinsă pentru frecvenţa de 159.2 Hz!

Aplicaţiile antirezonanţei

Este bine de ştiu că antirezonanţa are un efect de amortizare (atenuare) a oscilaţiilor circuitelor pur LC, precum cele paralel. La începutul acestui capitol am observat cum un condensator şî o bobină conectate direct împreună se comportă precum un pendul, schimbând tensiune şi curent între ele precum un pendul schimbă energia potenţială cu cea cinetică, alternatov. Într-un circuit oscilator perfect (rezistenţă zero), această oscilaţie poate continua la infinit, la fel ca în cazul unui pendul fără frecări, ce ar putea oscila la infinit la frecvenţa sa de rezonanţă. Dar aceste dispozitive fără frecare sunt foarte greu de găsit în realitate, şi la fel este şi cazul circuitelor oscilatoare. Pierderea de energie prin rezistenţă (sau alte tipuri de pierdere) într-un circuit LC va duce la atenuarea amplitudinii oscilaţiilor până acestea se „sting”. Dacă într-un circuit oscilator, există suficiente pierderi de energie, acesta nu va rezona deloc.

Efectul de antirezonanţă este mai mult decât o simplă curiozitate: poate fi extrem de utilă la eliminarea oscilaţiilor nedorite din circuitele ce conţin inductanţe sau capacităţi parazite, precum este cazul majorităţii circuitelor. Să luăm ca şi exemplu următorul circuit, al cărei constantă de timp este L/R:

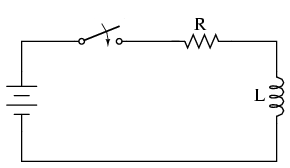
Idea acestui circuit este simplă: încărcarea bobinei atunci când întrerupătorul este închis. Rata (viteza) de încărcare a bobine depinde de raportul L/R, cunoscut sub numele de constante de timp al circuitului, măsurată în secunde. Totuşi, dacă ar fi să construim fizic un asfel de circuit, am descoperi oscilaţii neaşteptate a tensiunii la bornele bobine atunci când întrerupătorul este închis. De ce se întâmplă acest lucru? Nu există niciun condensator în circuit, prin urmare, cum putem avea oscilaţie rezonantă folosind doar o bobină, un rezistor şi o baterie?

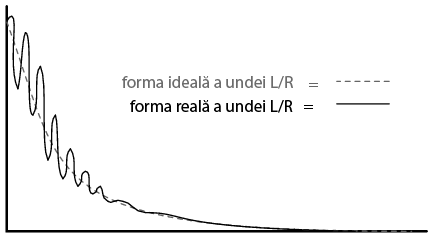
Toate bobinele prezintă o anumită capacitate parazită datorită modului de realizare a înfăşurărilor. De asemenea, conductorii folosiţi pentru realizarea circuitului, prezintă şi ei o anumită capacitate parazită. Cu toate că proiectarea „curată” a circuitelor electrice elimină mare parte dintre aceste capacităţi parazite, aceasta nu poate fi niciodată eliminată integral. Dacă acest lucru cauzează probleme de rezonanţă (oscilaţii nedorite), un mod de combatere al acestui efect este prin adăugarea rezistenţelor. Dacă un rezistor, R, este suficient de mare, acesta va duce la o situaţie de antirezonanţă, disipând suficientă energie pentru anularea, sau diminuarea efectelor oscilaţiei datorate combinaţiei dintre inductanţă şi capacităţile parazite.

Este interesant de menţionat faptul că, principiul utilizării rezistenţei pentru eliminarea efectelor nedorite ale rezonanţei este des folosit în conceperea sistemlor mecanice, unde orice obiect aflat în mişcare reprezintă un potenţial rezonator. O aplicaţie extrem de des întâlnită este folosirea amortizoarelor la automobile. Fără amortizoare, automobilele ar vibra necontrolat la frecvenţa de rezonanţă, atunci când ar întâlni o denivelare în asfalt, de exemplu. Rolul amortizorului este de a introduce un efect antirezonant puterni prin disiparea energiei pe cale hidraulică, în acelaşi fel în care un rezistor disipă energie pe cale electrică. p>