< Curent continuu
10 Analiza retelei
10.1 Ce înseamnă analiza unei reţele
General vorbind, analiza reţelei este o metodă matematică folosită pentru analiza unui circuit (o „reţea” de componente interconectate). În multe cazuri, tehnicianul sau inginerul, va întâlni circuite ce conţine surse de putere multiple sau configuraţii ale componentelor ce nu se pot simplifica prin metodele serie/paralel. În aceste cazuri este necesară utilizarea altor mijloace. Acest capitol prezintă câteva tehnici folositoare pentru analiza unor asfel de circuite complexe.
Pentru ilustrarea faptului că un ciruit relativ simplu poate fi imposibil de redus în subcircuite serie sau paralel, să luam următorul circuit serie-paralel ca şi exemplu:
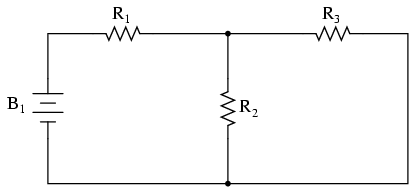
Pentru analiza circuitului de mai sus paşii sunt următorii: găsirea rezistenţei echivalente pentru R2 şi R3 în paralel; adăugarea rezistorului R1 în serie pentru aflarea rezistenţei echivalente totale; cunoscând tensiunea bateriei B1 şi rezistenţa totală a circuitului, putem afla curentul total folosind legea lui Ohm (I=E/R); folosirea valorii curentului pentru calcularea căderilor de tensiune din circuit. O procedură destul de simplă până la urma.
Totuşi, dacă adăugăm o singură baterie în circuit, problema analizei circuitului se complică:
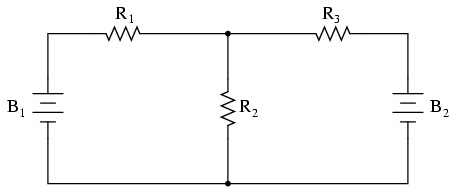
Rezistorii R2 şi R3 nu mai sunt conectaţi în paralel unul cu celălalt, pentru că bateria B2 a fost introdusă în ramura de circuit a lui R3. Dacă suntem şi mai atenţi, putem observa că în acest circuit nu există doi rezistori legaţi direct în serie sau paralel unul cu celălalt. Acesta şi este dificultatea problemei: în analiza circuitelor serie-paralel, primul pas era identificarea rezistorilor în serie sau paralel, reducându-i la o rezistenţă echivalentă la următorul pas. Dar dacă niciun rezistor nu este legat în serie sau paralel cu un altul, ce putem face?
Este evident faptul că reducerea acestui circuit relativ simplu, cu doar trei rezistori, este imposibil de realizat prin metoda analizei circuitelor serie-paralel: este ceva cu totul diferit. Totuşi, acesta nu este singurul tip de circuit ce sfidează analiza serie-paralel.
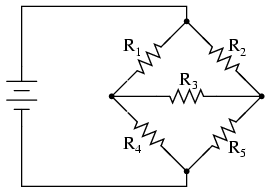
În acest caz avem un circuit în punte; pentru simplitatea exemplului presupunem că nu este echilibrat (raportul R1/R4 nu este egal cu raportul R2/R5). Dacă puntea ar fi echilibrată, curentul prin R3 ar fi zero, prin urmare circuitul s-ar putea reduce la o combinaţie serie-paralel (R1–R4 // R2–R5). Din păcate, iruce curent prin R3 face imposibilă aplicarea analizei serie-paralel. Rezistorul R1 nu este în serie cu R4 datorită existenţei unei alte căi pentru curgerea electronilor, prin R3. Dar nici R2 nu este în serie cu R5 din aceleaşi motive. De asemenea, R1 nu este în paralel cu R2 pentru că existenţa rezistorului R3 separă terminalii celor doi rezistori în partea de jos. Nici R4 nu este în paralel cu R5.
Deşi s-ar putea să nu fie evident în acest moment, problema o reprezintă existenţa prea multor cantităţi necunoscute. Într-o combinaţie serie-paralel cel puţin, exista o metodă de aflare a căderii de tensiune şi a rezistenţei totale, calcularea curentului fiind apoi posibilă utilizând acest valori. În cazul circuitelor de mai sus, există mai mult de o singură variabilă (parametru) necunoscut în cea mai simplă configuraţie a circuitului posibilă.
În cazul unui circuit cu două baterii, este imposibil să ajungem la valoarea „rezistenţei totale”, datorită existenţei a două surse de putere ce furnizează tensiune şi curent (am avea nevoie de două rezistenţe „totale” pentru a continua cu aplicarea legii lui Ohm). În cazul punţii dezechilibrate, există o rezistenţă totală la bornele bateriei, dar curentul total ce împarte în proporţii necunoscute în cadrul punţii, asfel că nu putem aplica legea lui Ohm pentru aflarea celorlalte valori din circuit.
Prin urmare, ce putem face în asfel de cazuri? Un prim răspuns este utilizarea unui proces matematic cunoscut sub numele de ecuaţii simultane sau sisteme de ecuaţii. Într-un scenariu cu o singură necunoscută, este suficientă existenţă unei singure relaţii pentru aflarea necunoscutei. Totuşi, atunci când dorim o rezolvare pentru mai multe necunoscute simultan, avem nevoie de un număr de ecuaţii egal cu numărul necunoscutelor. Rezolvarea unor asfel de ecuaţii se poate dovedi destul de dificilă în unele cazuri. Din fericire, în cele ce urmează, vom prezenta unele metode de analiză a circuitelor pentru evitatea folosirii acestor sisteme de ecuaţii. Aceste metode poartă numele de teoreme de analiză a reţelelor.
10.2 Metoda ramurii de curent
Folosind aceasta metodă, presupunem şi indicăm un sens al curenţilor prin circuit şi scriem apoi ecuaţiile ce descriu relaţiile dintre aceştia folosind legile lui Ohm şi Kirchhoff. În momentul în care avem câte o ecuaţie pentru fiecare curent necunoscut, putem rezolva sistemul de ecuaţii pentru determinarea tuturor curenţilor şi prin urmare a tuturor căderilor de tensiune din reţea.
Să folosim următorul circuit pentru ilustrarea metodei:
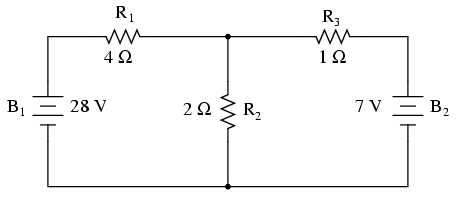
Primul pas este alegerea unui nod din circuit ca şi punct de referinţă pentru curenţii necunoscuţi:
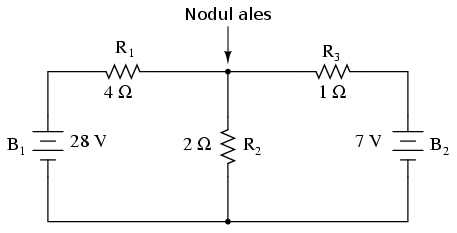
Ghicim apoi direcţia curenţilor din acest nod, notând curenţii cu I1, I2 şi I3. Nu este neapărat ca direcţiile acestea să fie cele corecte (reale), în acest moment acestea sunt pur speculative. Vom ştii dacă intuiţia noastră a fost greşită în momentul rezolvării ecuaţiilor matematice pentru curenţi; orice direcţie greşită va apărea în ecuaţii cu semnul minus.
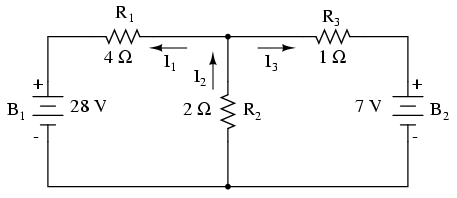
Legea lui Kirchhoff pentru curenţii (LKC) spune că suma algebrică a tuturor curenţilor ce intră şi iers dintr-un nod de reţea trebuie să fie egală cu zero, prin urmare putem introduce curenţii I1, I2 şi I3 într-o singură ecuaţie. Vom nota toţi curenţii ce intră într-un nod cu semnul pozitiv şi toţi curenţii ce ies dintr-un nod cu semnul negativ (acesta este doar o convenţie; inversând semnele rezultatul final va fi exact acelaşi):
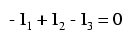
Pasul următor este notarea tuturor semnelor căderilor de tensiune în funcţie de sensul presupus al curenţilor. Ţineţi minte că partea din „amonte” a rezistorului va fi tot timpul negativă, iar partea din „aval” tot timpul pozitivă întrucât electronii posedă o sarcină negativă.
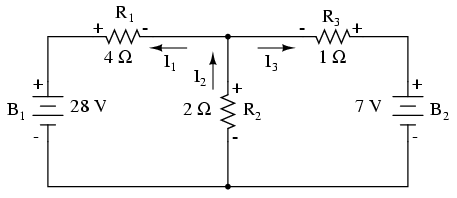
Desigur, polaritatea bateriilor rămâne aceeiaşi. Nu este nicio problemă dacă polaritatea rezistorului nu se „asortează” cu cea a bateriei atât timp cât polaritatea rezistorului este bazată pe direcţia presupusă de curgere a curentului prin acesta. Toate calculele efectuate de acum încolo se vor baza pe direcţia presupusă a curenţilor prin nodul ales.
Legea lui Kirchhoff pentru tensiune (LKU) spune că suma algebrică a tuturor căderilor de tensiune dintr-o buclă de reţea trebuie să fie egală cu zero. Pentru a obţine ecuaţiile folosind LKU, trebuie să introducem valorile căderilor de tensiune ca şi cum le-am fi măsurat cu un voltmetru real. Putem începe parcurgerea buclei din orice punct dorim; în cazul de faţa începem de la bornele bateriei şi continuăm în sens invers acelor de ceasornic până ajungem în punctul de unde am plecat:
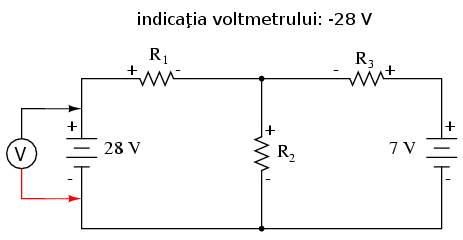
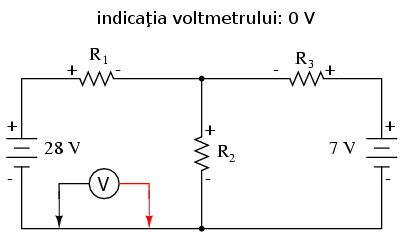
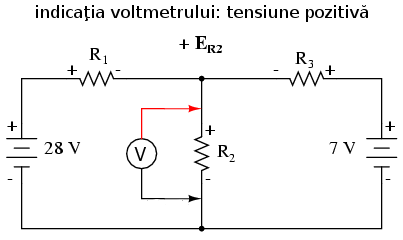
După ce am percurs întreaga buclă din stânga, adunăm aceste valori ale tensiunii pentru a forma o ecuaţie:
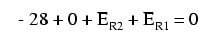
Evident, nu cunoaştem încă valoarea căderilor de tensiune la bornele rezistorilor R1 şi R2 aşa că nu putem introduce valorile lor reale în ecuaţie în acest moment. Totuşi, ştim faptul că suma tuturor acestor căderi de tensiune trebuie să fie egală cu zero, prin urmare ecuaţia este adevărată şi o putem folosi mai departe în analiza noastră. Putem dezvolta ecuaţia înlocuind tensiunile necunoscute cu produsul dintre curenţii necunoscuţi, I1 şi I2, şi valoarea rezistorilor prin care aceştia trec, folosind legea lui Ohm (E=IR). Eliminăm de asemenea şi valoarea 0 din sumă:
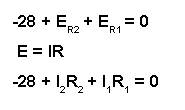
Din moment ce cunoaştem valorile tuturor rezistorilor în ohmi, putem să înlocui acele valori în evuaţie pentru uşurinţa calculelor:
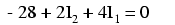
Motivul pentru care am redus ecuaţia în acest fel (până la urmă, avem tot două necunoscute) este folosirea aceloraşi variabile necunoscute ce le-am folosit şi în evuaţia LKC de mai sus (curenţi). Aceast pas este necesar pentru aflarea soluţiei sistemului final de ecuaţii.
Aplicând aceeiaşi paşi şi pentru bucla din dreapta, obţinem o altă ecuaţie.
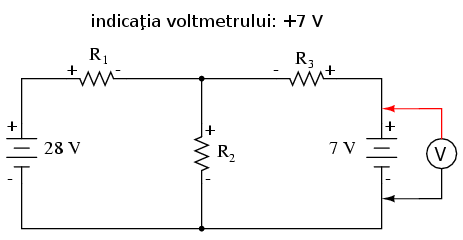
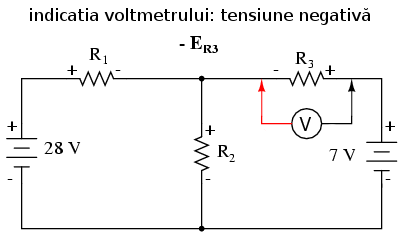
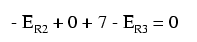
Cunoscând faptul că tensiunea de pe fiecare rezistor poate şi trebuie să fie exprimată ca şi produsul dintre curent şi rezistenţa fiecarărui rezistor, putem rescrie ecuaţia de mai sus asfel:
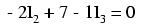
În acest moment avem un sistem matematic format din trei ecuaţii (o ecuaţie LKC şi două ecuaţii LKT) şi trei necunoscute:
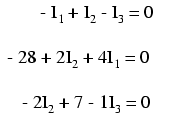
Putem rescrie ecuaţiile de mai sus trecând în dreapta valorile cunoscute (constantele ecuaţiilor) şi lăsând în partea stângă valorile necunoscute (I1, I2 şi I3), trecând explicit toţi coeficienţii pentru claritate. Putem oberva că toate cele trei variabile sunt prezente în toate cele trei ecuaţii:
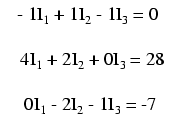
Rezolvând ecuaţiile de mai sus, ajungem la soluţia celor trei valori necunoscute ale curenţilor:
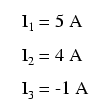
Prin urmare, valoarea curentului I1 este de 5 amperi, I2 4 amperi iar I3 minus 1 amper. Dar ce înseamnă curent „negativ”? În acest caz, înseamnă că intuiţia noastră cu privire la direcţia curentului a fost inversă faţa de direcţia reală. Revenind la circuitul iniţial, putem reface schema acestuia schimbând direcţia curentului I3 schimbând în acelaşi timp şi polaritatea căderii de tensiune de pe rezistorul R3.
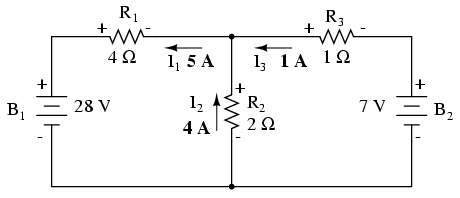
Observăm faptul că, prin bateria B2 curentul circulă în sens invers datorită tensiunii mai ridicate a bateriei B1. În ciuda faptului că polaritatea bateriei încercă să împingă electronii prin acea ramură de circuit, electronii sunt defapt forţaţi să se deplaseze în sens contrar datorită tensiunii superioare a bateriei B1. Înseamnă acest lucru faptul că întotdeauna bateria mai puternică va „câştiga” iar curentul prin bateria mai slabă va fi forţăt tot timpul în sens contrar? Nu! Acest lucru depinde de fapt atât de diferenţe de tensiune dintre cele două bateri cât şi de valoarea rezistorilor din circuit. Singura metodă sigură de aflare a comportamentului circuitului este analiza matematică a acestuia.
Cunoscând acum valoarea tuturor curenţilor din circuit, putem calcula căderile de tensiune la bornele tuturor rezistorilor folosind legea lui Ohm (E=IR):
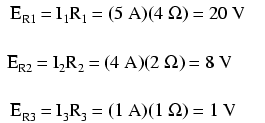
Paşii pentru aplicarea metodei ramurii de curent:
- Alegearea unui nod şi a direcţiilor curenţilor (aleator)
- Scrierea ecuaţiei legii lui Kirchhoff pentru curent în acel nod
- Notarea polarităţilor căderilor de tensiune în funcţie de direcţia aleasă a curenţilor
- Scrierea ecuaţiilor legii lui Kirchhoff pentru fiecare buclă din circuit, înlocuind căderea de tensiune de pe fiecare rezistor (E) cu produsul IR în fiecare ecuaţie
- Aflarea curenţilor necunoscuţi de pe fiecare ramură (rezolvarea sistemului de ecuaţii)
- Dacă oricare dintre soluţii este negativă, atunci direcţia pe care am intuit-o la punctul 1 este greşită!
- Calcularea căderilor de tensiune la bornele tuturor rezistorilor (E=IR)
10.3 Metoda buclei de curent
Metoda buclei de curent sau metoda ochiului de curent este asemănătoare metodei ramurii de curent prin faptul că foloseşte un sistem de ecuaţii descris de legea lui Kirchhoff pentru tensiune şi legea lui Ohm pentru determinarea curenţilor necunoscuţi din circuit. Diferă de metoda ramurii de curent prin faptul că nu utilizează legea lui Kirchhoff pentru curent şi de obicei este nevoie de mai puţine variabile şi ecuaţii pentru rezolvare, ceea ce reprezintă un avantaj.
Metoda convenţională
Să vedem cun funcţionează această metodă folosind acelaşi circuit:

Primul pas în metoda buclei este identificarea „buclelor” din circuit asfel încât să cuprindem toate componentele. În circuitul de mai sus, prima bucla va fi cea formată de B1, R1, şi R2, iar cea de a doua din B3, R2, and R3. Partea cea mai ciudată a acestei metode este imaginarea circulaţiei curenţilor prin fiecare dintre aceste bucle.
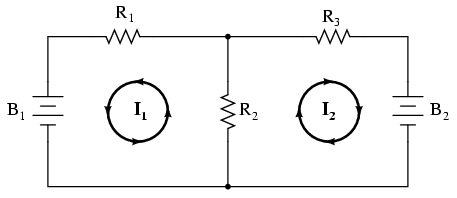
Alegerea direcţiei fiecărui curent este complet arbitrară precum în cazul metodei ramurii de curent, dar ecuaţiile rezultate sunt mai uşor de rezolvat dacă avem aceeiaşi direcţie prin componentele aflate la intersecţia celor două bucle formate (putem observa faptul că atât curentul I1 cât şi I2 trec prin rezistorul R2 de jos în sus în locul în care se intesectează). Dacă direcţia curentului presupusă iniţial se dovedeşte a fi greşită, acest lucru se va observa în soluţia finală prin faptul că valoarea va fi negativă.
Următorul pas este notarea tuturor polarităţilor căderilor de tensiune la bornele rezistorilor în funcţie de direcţia curenţilor indicată de bucle. Ţineţi minte că partea din „amonte” a rezistorului va fi tot timpul negativă, iar partea din „aval” tot timpul pozitivă întrucât electronii posedă o sarcină negativă. Polarităţile bateriei depind desigur de orientarea lor în diagramă şi pot să corespundă sau să nu corespundă cu polarităţile rezistorilor:
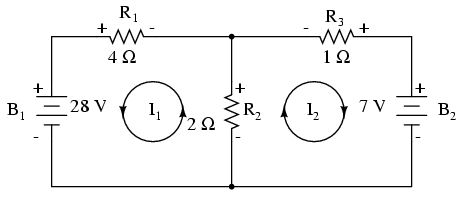
Utilizând legea lui Kirchhoff pentru tensiune, putem parcurge fiecare dintre cele două bucle, generând ecuaţii în funcţie de căderile de tensiune ale coponentelor şi de polarităţi. La fel ca în cazul metodei ramurii de curent, vom desemna căderea de tensiune a unui rezistor ca produsul dintre rezistenţa acestuia (în ohmi) şi curentul buclei respective (I1 sau I2 în acest caz), a cărei valoare nu este cunoscută în acest moment. Când cei doi curenţi se intersectează (cazul rezistenţei R2), vom scrie acel termen al ecuaţie ca produsul dintre căderea de tensiune pe acel component şi suma celor doi curenţi ai buclelor (ER2*(I1 + I2)).
Începem cu bucla din stânga din colţul stânga sus şi parcurgem întregul ochi de reţea în direcţia inversă acelor de ceasornic (direcţia este pur arbitrară), obţinând următoarea ecuaţie:
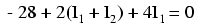
Observaţi faptul că prin rezistorul R2 curentul care trece este de fapt suma curenţilor celor două bucle( I1 şi I2). Acest lucru se datorează faptul că ambii curenţi trec prin R2 în aceeiaşi direcţie. Simplificând ecuaţia obţinem:
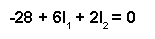
În acest moment avem o singură ecuaţie şi/cu două necunoscute. Acest lucru înseamnă ca mai avem nevoie de încă o evuaţie pentru a determina curenţii buclelor. Această ecuaţia o obţinem prin parcurgerea buclei din dreapta a circuitului, şi obţinem:
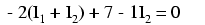
Simplificând ecuaţia cum am făcut şi înainte, obţinem:
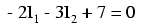
Având două ecuaţii putem folosi metode matematice pentru determinarea necunoscutelor I1 şi I2:
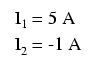
Dar, atenţie, aceste valori ale curenţilor sunt valabile pentru bucle şi nu sunt curenţii efectivi ai ramurilor. Să ne întoarcem la circuitul iniţial pentru a vedea care este relaţia dintre ei.
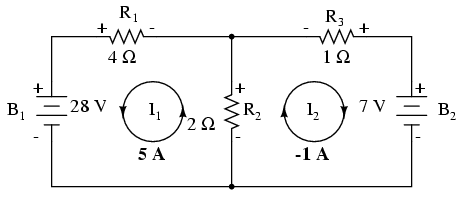
Rezultatul de minus 1 amper pentru curentul buclei I2 înseamnă că direcţia indicată iniţial (aleator) este incorectă. În realitate, direcţia curentului I2 este contrară acesteia (observaţi modificarea sensului buclei pe desen!)
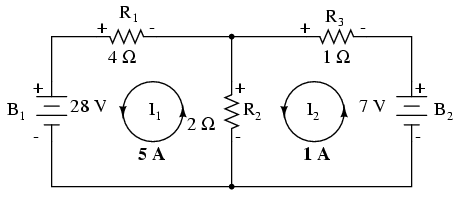
Această modificare a direcţiei curentului faţă de ceea ce am presupus iniţial va modificat polaritatea căderilor de tensiune pe rezistorii R2 şi R3 datorită curentului I2. De aici putem deduce curentul prin R1, 5 amperi, căderea de tensiune (I*R) 20 de volţi. De asemenea, curentul prin R3 este 1 amper, cu o cădere de tensiune de 1 volt. Dar ce se întâmplă în cazul rezistorului R2?
Curentul de buclă I1 trece prin R2 de jos în sus, iar curentul I2 de sus în jos. Pentru a determina curentul real prin R2, trebuie să observăm foarte atent interacţiunea dintre curenţii celor două bucle, I1 şi I2 (în acest caz sunt în opoziţie); valoarea finală va fi suma algerbrică a celor doi. Din moment ce I1 are 5 amperi într-o direcţie şi I2 1 amper în direcţia opusă, curentul real prin R2 este diferenţa celor doi, adică 4 amperi şi trece prin R2 de jos în sus:
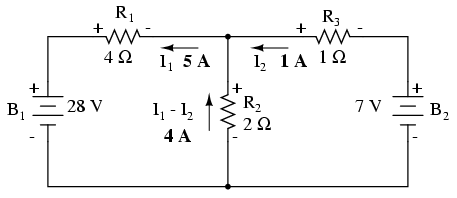
Cu un curent de 4 amperi prin R2 rezultă o cădere de tensiune de 8 volţi.
Exemplu aditional
Principalul avantaj al metodei buclei de curent este că în general soluţia unei reţele mari poate fi găsită cu relativ puţine ecuaţii şi puţine necunoscute. Pentru circuitul analizat de noi a fost nevoie de 3 ecuaţii folosind metoda ramurii de curent şi doar două folosind metoda buclei de curent. Acest avantaj creşte semnificativ atunci când reţeau creşte în complexitate:
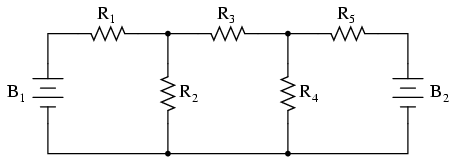
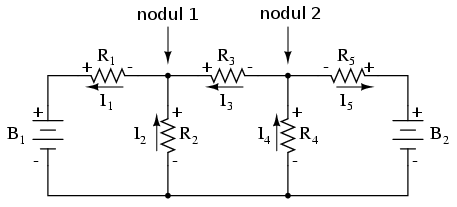
Pentru rezolvara acestui circuit folosind metoda ramurii de curent, am avea nevoie de 5 variabile pentru fiecare curent posibil din circuit (de la I1 la I5) şi prin urmare 5 ecuaţii pentru aflarea soluţiei, două pentru LKC şi trei pentru LKT:
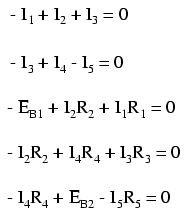
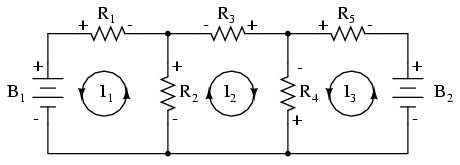
În schimb, folosind metoda buclei de curent avem doar trei necunoscute şi prin urmare doar trei ecuaţii de rezolvat pentru rezolvarea reţelei, ceea ce constituie un avantaj:
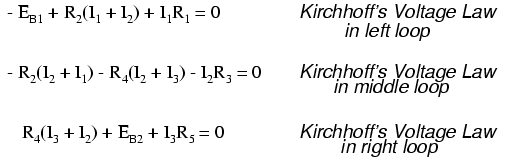
Paşii pentru aplicarea metodei ramurii de curent:
- Trasarea buclelor de curent în circuit asfel încât să fie cuprinse toate componentele
- Noatarea polarităţii căderilor de tensiune de pe rezistori în funcţie de direcţiile curenţilor de bucla aleşi
- Scrierea ecuaţiilor legii lui Kirchhoff pentru tensiune în cazul fiecărei bucle din circuit, înlocuind tensiunea (E) cu produsul dintre curent şi rezistenţă (IR) pentru fiecare rezistor din ecuaţie. Acolo unde doi curenţi de buclă se intersectează unul cu celălalt printr-un comonent, curentul se exprimă ca şi sumă algebrică dintre cei doi curenţi (ex. I1 + I2) dacă au aceeiaşi direcţie prin component; în caz contrar, curentul se va exprima ca şi diferenţă (I1 - I2)
- Rezolvare sistemului de ecuaţii rezultat şi aflarea curenţilor de buclă
- Dacă oricare dintre soluţii este negativă, înseamnă că direcţia iniţială presupusă pentru curent este greşită!
- Adunarea algebrică a curenţilor de buclă pentru aflarea curenţilor prin componentele prin care trec mai mulţi curenţi de buclă
- Aflarea căderilor de tensiune pe toţi rezistorii (E=IR)
10.4 Metoda nodului de tensiune
Metoda nodului de tensiune pentru analiza circuitelor determină tensiunea nodurilor în funcţie de ecuaţiile legii lui Kirchhoff pentru curent. Această analiză arată puţin ciudat pentru că necesită înlocuirea surselor de tensiune cu surse echivalente de curent. De asemenea, valorile rezistorilor în ohmi sunt înlocuite prin conductanţele ecivalente în siemens, G = 1/R. Unitatea de măsură pentru conductanţă este siemens-ul, S=Ω-1
Exemplul 1
Începem cu un circuit ce conţine surse de tensiune convenţionale. Un punct comun E0 este ales ca şi punct de referinţă. Tensiunile pentru celelalte noduri, E1 şi E2 sunt calculate în funcţie de acest punct.
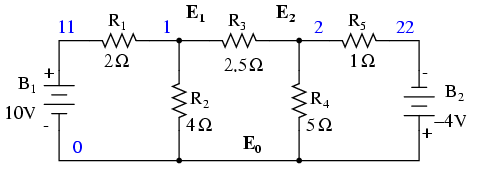
O sursă de tensiune în serie cu o rezistenţă trebuie să fie înlocuită de o sursă de curent echivalentă în paralel cu o rezistenţă. Vom scrie apoi ecuaţiile LKC pentru fiecare nod. Partea dreaptă a ecuaţiei reprezintă valoarea sursei de curent ce alimentează nodul respectiv. Circuitul modificat arată asfel:
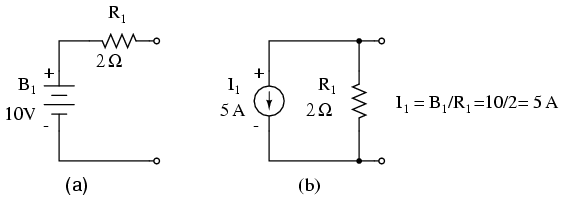
Înlocuim rezistenţa rezistorilor în ohmi cu conductanţa acestora în siemens:
I1 = E1/R1 = 10/2 = 5 A I2 = E2/R5 = 4/1 = 4 A G1 = 1/R1 = 1/2 Ω = 0.5 S G2 = 1/R2 = 1/4 Ω = 0.25 S G3 = 1/R3 = 1/2.5 Ω = 0.4 S G4 = 1/R4 = 1/5 Ω = 0.2 S G5 = 1/R5 = 1/1 Ω = 1.0 S
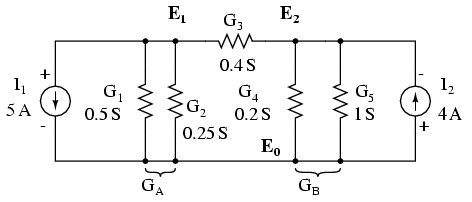
Conductanţele paralele (rezistorii) pot fi combinaţi prin adunarea conductanţelor. Deşi nu vom redesena circuitul, putem deja aplica metoda nodului de tensiune:
GA = G1 + G2 = 0.5 S + 0.25 S = 0.75 S GB = G4 + G5 = 0.2 S + 1 S = 1.2 S
Pentru dezvoltarea unei metode generale, vom scrie ecuaţiile LKC în funcţie de tensiunile necunoscute ale nodurilor 1 şi 2, V1 şi V2 de această dată.
GAE1 + G3(E1 - E2) = I1 (1)
GBE2 - G3(E1 - E2) = I2 (2)
(GA + G3 )E1 -G3E2 = I1 (1)
-G3E1 + (GB + G3)E2 = I2 (2)
Suma conductanţelor conectate la primul nod este este coeficientul pozitiv al primei tensiuni din ecuaţia (1). Suma conductanţelor conectate la cel de al doilea nod este coeficientul pozitiv al celei de a doua tensiuni din ecuaţia (2). Ceilalţi coeficienţi sunt negativi, reprezentând conductanţele dintre noduri. Pentru ambele ecuaţii, partea dreaptă a ecuaţiei este egală cu sursa de curent respectivă conectată la nod. Această metodă ne permite să scriem rapid ecuaţiile prin inspecţie şi duce la următoarele reguli pentru aplicarea metodei nodului de tensiune.
- Înnlcuirea surselor de tensiune în serie cu un rezistor cu o sursă echivalentă de curent şi un rezistor în paralel
- Schimbarea valorilor rezistorilor în conductanţe
- Selectarea unui nod de referinţă (E0)
- Desemnarea unor tensiuni necunoscute pentru nodurile rămase, (E1)(E2) … (EN)
- Scrierea unei ecuaţii LKC pentru fiecare nod, 1, 2, … N. Coeficientul pozitiv a primei tensiuni din prima ecuaţie este suma conductanţelor conectate la primul nod. Coeficientul pentru a doua tensiune din a doua ecuaţie este suma conductanţelor conectate la acel nod. Acelaşi lucru este valabil şi pentru a treia tensiune în ecuaţia a treia şi pentru celelalte ecuaţii. Aceşti coeficienţi se găsesc pe o diagonală.
- Toţi ceilalţi coeficienţi ai ecuaţiei sunt negativi, reprezentând conductanţele dintre noduri. În prima ecuaţie, coeficientul al doile reprezintă conductanţa dintre nodul 1 şi nodul 2, al treilea coeficient reprezintă conductanţă dintre nodul 1 şi nodul 3. Acelaşi lucru este valabil şi pentru celelalte ecuaţii
- Partea din dreapta a ecuaţiilor reprezintă sursa de curent conectată la nodurile respective
- Rezolvarea sistemului de ecuaţii şi aflarea tensiunilor nodurilor necunoscute
Pentru figura de mai sus, ecuaţiile arată asfel:
(0.5+0.25+0.4)E1 -(0.4)E2 = 5
-(0.4)E1 +(0.4+0.2+1.0)E2 = -4
(1.15)E1 -(0.4)E2 = 5
-(0.4)E1 +(1.6)E2 = -4
E1 = 3.8095
E2 = -1.5476
Exemplul 2
Circuitul de mai jos are trei noduri. Conductanţele nu apar pe desen, dar G1=1/R1, etc.
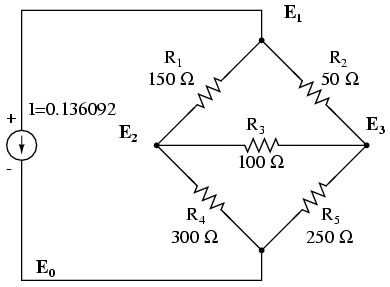
Există trei noduri pentru care putem scrie ecuaţii. Coeficienţii sunt pozitivi pentru E1 (ecuaţia 1), E2 (ecuaţia 2) şi E3 (ecuaţia 3). Acestea sunt sumele tuturor conductanţelor conectate la nodurile respective. Toţi ceilalţi coeficienţi sunt negativi, reprezentând conductanţa între noduri. Partea din dreapta a ecuaţiei reprezintă sursa de curent, 0.136092 amperi, singura sursă pentru nodul 1. Celelalte ecuaţii au zero în partea dreapta datorită lipsei unei surse de tensiune.
(G1 + G2)E1 -G1E2 -G2E3 = 0.136092
-G1E1 +(G1 + G3 + G4)E2 -G3E3 = 0
-G2E1 -G3E2 +(G2 + G3 + G5)E3 = 0
Se poate observa că diagonala matricii formate are coeficienţi pozitivi. Toţi ceilalţi coeficienţi sunt negativi.
Soluţia este E1 = 24.000 V, E2 = 17.655 V, E3 = 19.310 V.
10.5 Teorema lui Millman
Prin intermediul teoremei lui Millman, circuitul este redesenat ca şi o reţea de ramuri paralele, fiecare ramură conţinând un rezistor sau o combinaţie serie baterie/rezistor. Această teoremă se poate aplica doar în cazul circuitelor ce pot suferi această modificare.
Exemplu
Avem (din nou) circuitul de mai jos:

Acelaşi circuit redesenat pentru aplicarea teoremei lui Millman:
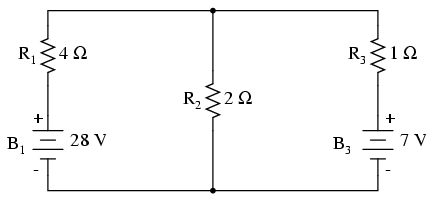
Luând în considerare rezisteţa şi tensiunea furnizată în fiecare ramură, putem folosi teorema lui Millman pentru aflarea căderilor de tensiune în toate ramurile. Chiar dacă nu există bateria B2, notaţia B3 pentru bateria din dreapta este pentru a scoate în evidenţă faptul că aceasta aparţine ramurii 3 din circuit!
Teorema nu este altceva decât o ecuaţie lungă aplicabilă oricărui circuit ce poate fi redesenat ca şi ramuri paralele, fiecare ramură cu propria sa sursă de tensiune şi rezistenţă în serie:
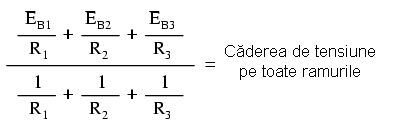
Înlocuind valorile din exemplul de mai sus ajungem la următorul rezultat:
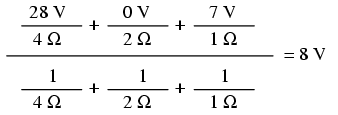
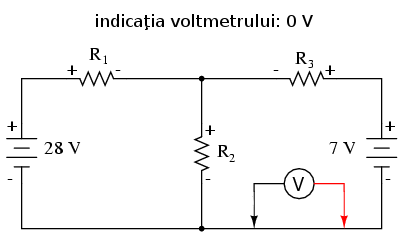
Valoarea rezultatului, 8 V, reprezintă căderea de tensiune pe toate ramurile:
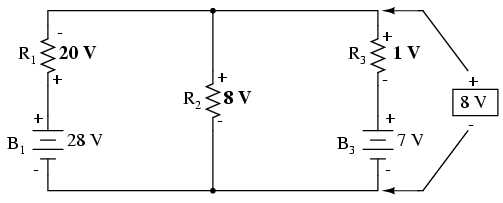
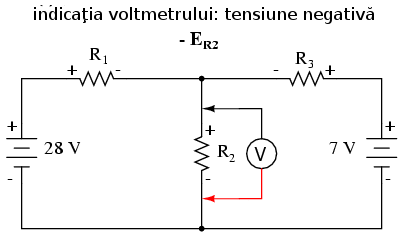
Polarităţile tuturor tensiunilor au ca şi referinţa acelaşi punct. În exemplul de mai sus, firul de jos este folosit ca şi punct de referinţă, prin urmare tensiunile pentru fiecare ramură au fost introduse în ecuaţie ca fiind pozitive (28 pentru R1, 0 pentru R2 şi 7 pentru R3).
Pentru aflarea căderilor de tensiune pe fiecare rezistor, tensiunea Millman (8 V în acest caz) trebuie compoarată cu tensiunea fiecărei surse din fiecare ramură, folosind principiul aditivităţii tensiunilor în serie:
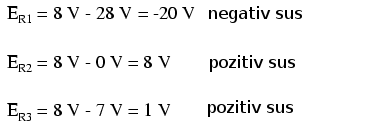
Pentru aflarea curenţilor prin fiecare ramură, aplicăm legea lui Ohm (I=E/R):
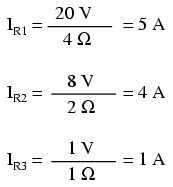
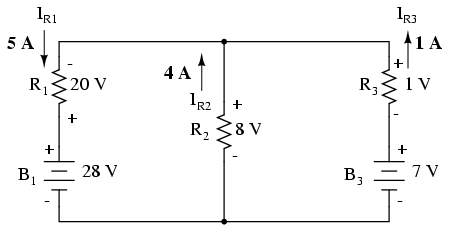
Direcţia curentului prin fiecare rezistor este determinată de polaritatea fiecărui rezistor şi nu de polaritatea bateriei, curentul putând fi forţat să de deplaseze invers printr-o baterie, precum în cazul bateriei B3. Acest lucru este bine de ţinut minte fiindcă teorema lui Millman nu ne oferă niciun indiciu cu privire la posibilitatea unei direcţii greşite a curenţilor precum este cazul metodelor ramurii de curent şi a buclei de curent. Trebuie să fim atenţi la polaritatea căderii de tensiune la bornele rezistorilor, determind de acolo direcţie de curgere a curentului.
10.6 Teorema superpoziţiei
Teorema superpoziţiei reprezintă acea viziune de geniu ce transformă un subiect complex într-o versiune simplă şi uşor de înteles.
Strategia constă în eliminarea rând pe rând a tuturor surselor de putere din circuit exceptând una singură, utilizând analiza serie/paralel pentru determinarea căderilor de tensiune şi a curenţilor din reţeaua modificată pentru fiecare sursă de putere separat. Apoi, după ce toate căderile de tensiune şi curenţii au fost determinaţi pentru fiecare sursă de tensiune funcţionând separat/independent în reţea, valorile sunt suprapuse una peste cealaltă (adunare algebrucă) pentru determinarea efectivă a curenţilor şi tensiunilor atunci când în circuit funcţionează toate sursele de putere împreună.
Exemplu
Să luăm acelaşi circuit ca şi exemplu:

Din moment ce avem două surse de putere în acest circuit, va trebui să calculăm două seturi de date pentru căderile de tensiune şi curent, un set pentru circuitul funcţionând doar cu sursa de tensiune de 28 de volţi…
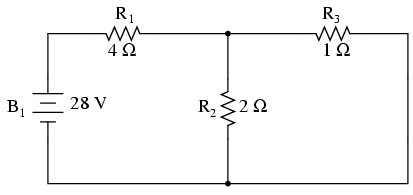
…celălalt pentru circuitul funcţionând doar cu bateria de 7 volţi:
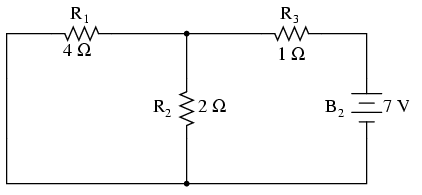
Atunci când redesenăm un circuit pentru analiza serie/paralel cu o singură sursă, toate celelalte surse de tensiune sunt înlocuite de fire (scurt circuit), şi toate sursele de curent sunt înlocuitr de circuite deschise. Din moment ce avem doar surse de tensiune (baterii) în circuitul de mai sus, toate sursele de putere inactive vor fi înlocuite de fire.
Analizând circuitul în care acţionează doar bateria de 28 de volţi, obţinem următoarele valori pentru tensiune şi curent:
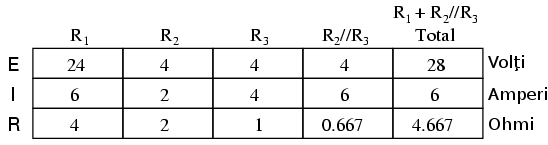
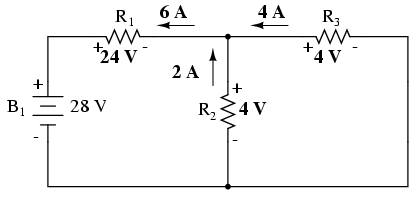
Analizând circuitul în care acţionează doar bateria de 7 de volţi, obţinem următoarele valori pentru tensiune şi curent:
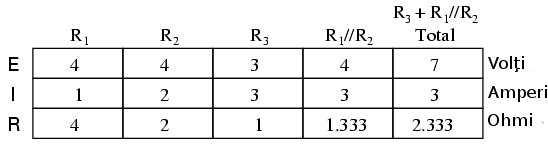
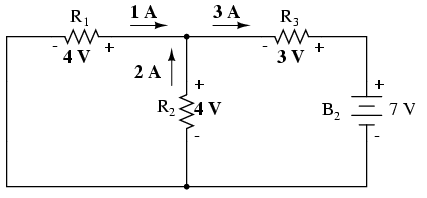
Atunci când realizăm suprapunerea, trebuie să fim foarte atenţi la polaritatea căderilor şi la direcţia curenţilor, pentru că aceste valori se adună algebric:
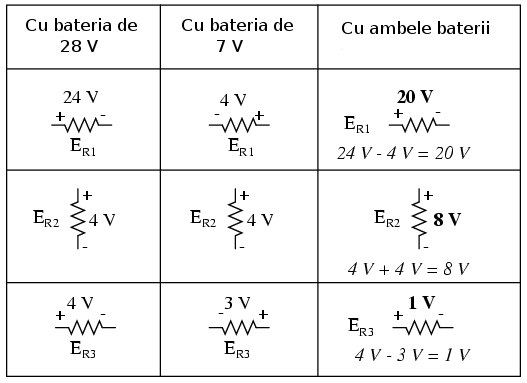
Aplicând aceste valori, rezultatul final arată asfel:
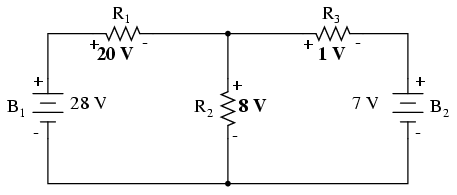
Acelaşi lucru este valabil şi în cazul curenţilor.
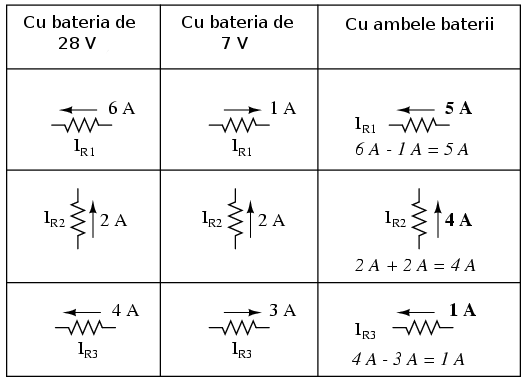
Folosind valorile aflate după aplicarea superpoziţiei, circuitul arată asfel:
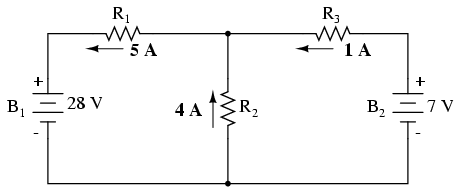
Simplu şi elegant în acelaşi timp. Totuşi, teorema superpoziţiei poate fi aplicată doar circuitelor ce pot fi reduse la combinaţii de circuite serie/paralel pentru fiecare sursă de putere (tensiune sau curent) în parte, şi doar atunci când ecuaţiile folosite sunt liniare. Acest lucru înseamnă ca teorema nu potate fi folosită decât pentru determinare tensiunii şi a puteri nu> şi a puterii! Puterile disipate în circuit, fiind funcţii neliniare, nu pot fi adunate algebric atunci când se consideră doar o sursă de putere. Aceeiaşi nevoie de liniaritate înseamnă ca teorema este inutilă în circuitele în care rezistenţa componentelor se modifică odată cu tensiunea sau temperatura, ca de exemplu becuri incandescente sau varistoare.
O altă condiţie este ca toate componentele să fie „bilaterale”, însemnând faptul că trebuie să se comporte exact le fel indiferent care este direcţia de deplasare a electronilor prin ele. Rezistenţele îndeplinesc această cerinţă, precum şi toate circuitele studiate până acum.
Teorema superpoziţiei se foloseşte şi în studiul circuitelor de curent alternativ (CA) şi circuitele cu amplificatoare semiconductoare, acolo unde de multe ori curentul alternativ este mixat (suprapus) peste curentul continuu. În asfel de cazuri putem analiza circuitul când doar sursa de curent continuu este prezentă în circuit şi atunci când doar cea de curent alternativ este prezentă; rezultatul final este superpoziţia celor două cazuri. Până una alta, folosind teorema superpoziţie nu mai suntem nevoiţi să folosim sistemele de ecuaţii pentru analiza circuitelor.
10.7 Teorema lui Thevenin
Teorema lui Thevenin susţine că orice circuit liniar poate fi simplificat, indiferent de complexitatea sa, la un circuit echivalent cu doar o singură sursă de tensiune şi o rezistenţă legată în serie. Semnificaţia termenului „liniar” este aceeiaşi ca şi în cazul teoriei superpoziţiei, unde toate ecuaţiile folosite trebuie să fie liniare. Dacă avem de a face cu componente pasive (rezistori, bobine şi condensatori) această condiţie este îndeplinită. Dar, există unele componente, precum cele semiconductoare, ce sunt neliniare. Aceste circuite le vom numi prin urmare neliniare
Teorema lui Thevenin este folosită în special pentru analiza sistemelor de putere şi alte circuite în care un rezistor din circuit (rezistorul de „sarcină”) este supus modificărilor; reclacularea circuitului este necesară cu fiecare valoare a rezistenţei de sarcină pentru determinarea tensiuni şi curentului prin el.
Exemplu
Să reluăm circuitul studiat până acum cu celelalte metode:

Să presupunem că rezistorul R2 este sarcina din acest circuit. Avem deja la dispoziţie patru metode pentru determinarea tensiunii şi curentului prin R2, dar niciuna dintre aceste metode nu este eficientă din punct de vedere al timpului de lucru. Imaginaţi-vă că aţi folosi aceste metode de fiecare dată când valoarea sarcinii (rezistenţei de sarcină) se schimbă (modificarea rezistenţei sarcinii este un lucru foarte des întâlnit în sistemele de putere). Această situaţie ar presupune multă muncă!
Teorema lui Thevenin înlătură temporar sarcina din circuitul iniţial transformând ceea ce rămâne într-un circuit echivalent compus dintr-o singură sursă de tensiune şi rezistenţe în serie. Rezistenţa de sarcină poate fi apoi re-conectată în acest „circuit Thevenin echivalent” şi se pot continua calculele pentru întreaga reţea ca şi cum nu ar fi decât un simplu circuit serie:
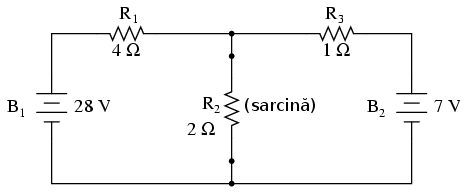
După conversia circuitului vom avea:
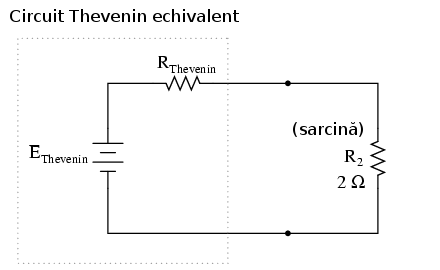
„Circuitul Thevenin echivalent” este echivalentul electric ale surselor şi rezistorilor B1, R1, R3 şi B2 văzute din cele două puncte de contact al rezistorului de sarcină R2. Acest circuit echivalent, dacă este dedus corect, se va comporta exact ca şi circuitul original. Cu alte cuvinte, curentul şi tensiunea sarcinii (R2) ar trebuie să fie exact aceeiaşi în ambele circuite. Rezistenţa R2 nu potate face diferenţa dintre reţeaua originală şi circuitul echivelnt, atâta timp cât EThevenin şi RThevenin au fost calculate corect.
Avantajul transformării constă în uşurinţa calculelor pentru circuitul simplificat, mult mai uşoară decât în cazul circuitului original. Primul pas este înlăturarea rezistenţei de sarcină din circuitul original şi înlocuirea acestuia cu un circuit deschis:
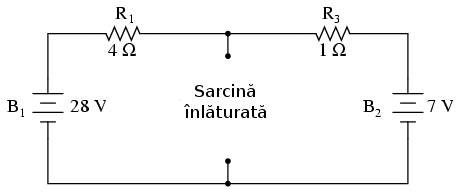
Apoi determinăm căderea de tensiune între punctele „fostei” sarcini, folind orice metode disponibile. În acest cazu, circuitul original, mai puţin sarcina, nu este altceva decât un circuit serie simplu cu două baterii; putem aplica prin urmare regulile circuitelor serie, legea lui ohm şi legea lui Kirchhoff pentru tensiune:
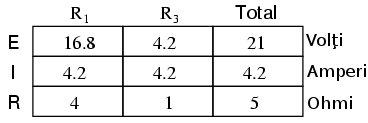
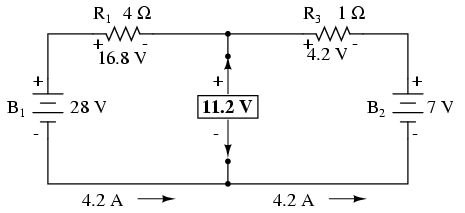
Căderea de tensiune între cele două puncte ale sarcinii poate fi dedusă din tensiunea bateriei şi căderea de tensiune pe una dintre baterii, fiind de 11.2 volţi. Aceasta este tensiunea Thevenin, EThevenin din circuitul echivalent:
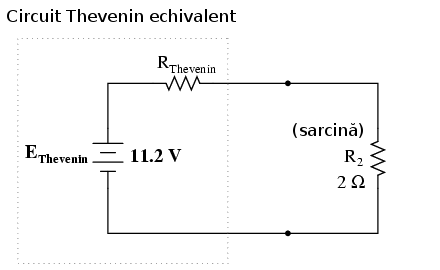
Pentru aflarea rezistenţei serie din circuitul echivalent, trebuie să luăm circuitul original, mai puţin sarcina, să înlăturăm sursele de putere (la fel ca în cazul teoremei superpoziţiei) şi să determinăm rezistenţa de la un terminal la celălalt:
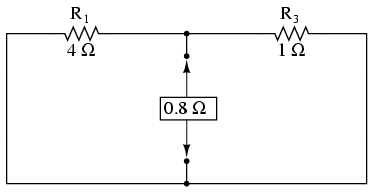
După înlăturarea celor două baterii, rezistenţa totală măsurată în această locaţie este egală cu rezistenţele R1 şi R3 în paralel: 0.8 Ω. Aceasta reprezintă rezistenţa Thevenin (RThevenin) pentru circuitul echivalent:
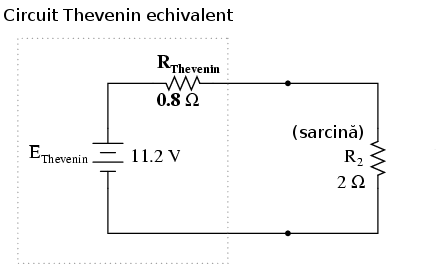
Cunoscând valoarea rezistorului (2 Ω) dintre cele două puncte de conexiune, putem determina căderea de tensiune şi curentul prin acesta, ca şi cum întregul circuit nu ar fi altceva decât un simplu circuit serie:
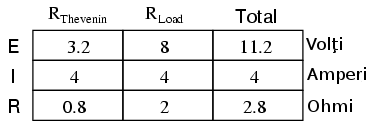
Putem oberva că valorile pentru curent şi tensiune (4 amperi, 8 volţi) sunt identice cu valorile găsite aplicând celelalte metode de analiză. De asemenea, valorile tensiunilior şi curenţilor pentru rezistenţa serie şi sursa Thevenin echivalente nu se aplică componentelor din circuitul original. Teorem lui Thevenin este folositoare doar pentru determinarea comportamentului unui singur rezistor din reţea: sarcina.
Paşii pentru aplicarea teoremei lui Thevenin:
- Găsirea sursei de tensiune Thevenin prin îndepărtarea sarcinii din circuitul original şi calcularea căderii de tensiune dintre punctele în care se afla sarcina iniţial
- Găsirea rezistenţei Thevenin prin îndepărtarea tuturor surselor de putere din circuitul original şi calcularea rezistenţei totale dintre cele două puncte
- Desenarea circuitului Thevenin echivalent, cu sursa de tensiune şi rezistenţa Thevenin în serie. Rezistorul de sarcină se re-introduce între cele două puncte (deschise) din circuit
- Aflarea căderii de tensiune şi a curentului prin rezistorul de sarcină folosind regulile circuitelor serie
10.8 Teorema lui Norton
Conform teoremei lui Norton este posibilă simplificarea oricărui circuit liniar, indiferent de complexitate, la un circuit echivalent dotat cu o singură sursă de curent şi o rezistenţă paralelă, ambele conectate la o sarcină. La fel ca în cazul teoremei lui Thevenin, termenul „liniar” are semnificaţia teoremei superpoziţiei: ecuaţiile implicate trebuie să fie liniare.
Exemplu
Circuitul iniţial este cel folosit şi în exemplele precedente, şi arată asfel:

Circuitul echivalent după aplicarea teoremei lui Norton va fi următorul:
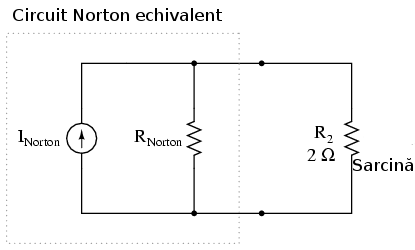
Sursa de curent este un component a cărui scop este furnizarea unei valori constante de curent, indiferent de valoarea tensiunii.
La fel ca în cazul teoremei lui Thevenin, întreg circuitul original, în afară de rezistenţa de sarcină, a fost redus la un circuit echivalent ce este mult mai uşor de analizat. Paşii folosiţi pentru calcularea sursei de curent, INorton, şi a rezistenţei Norton, RNorton, sunt de asemenea similari teoremei precedente.
Primul pas este identificarea rezistenţei de sarcină şi înlăturarea acesteia din circuitul original:

Pentru aflarea curentului Norton, plasăm un fir (scurt circuit) între cele două puncte ale sarcinii şi determinăm curentul rezultat. Observaţi că acest pas este exact invers în teorema lui Thevenin, unde am înlocuit sarcină cu un circuit deschis:
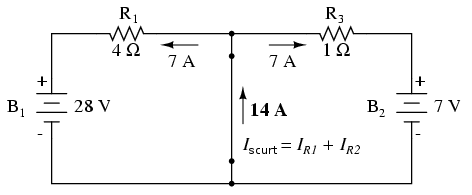
Acum avem o cădere de 0 volţi între punctele de conexiune a sarcinii (înăturate), ceea ce înseamă că valoarea curentului prin R1 depinde doar de tensiunea bateriei B1 şi de valoarea rezistorului R1: 7 amperi (I=E/R). Acelaşi lucru este valabil şi în partea dreapta a circuitului, unde curentul este tot 7 amperi. Prin urmare, curentul total prin scurt circuitul sarcinii este de 14 amperi şi reprezintă curentul sursei Norton (INorton).
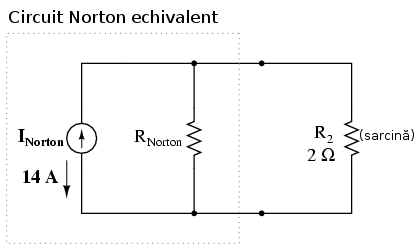
Din nou, direcţia săgeţii unei surse de curent este contrară deplasării reale a electronilor printr-un circuit, notaţie ce o folosim în această carte.
Pentru calcularea rezistenţei Norton, procedăm precum în cazul teoremei lui Thevenin: luăm circuitul original, fără rezistenţa de sarcină, îndepărtăm sursele de putere conform principiului aplicat în cadrul teoremei superpoziţiei (sursele de tensiune le înlocuim cu scurt circuit iar sursele de tensiune cu circuit deschis) şi aflăm apoi rezistenţa totală dintr-un punct al sarcinii la celălalt (cei doi rezistori legaţi în paralel):

În acest moment circuitul Norton echivalent arată asfel:
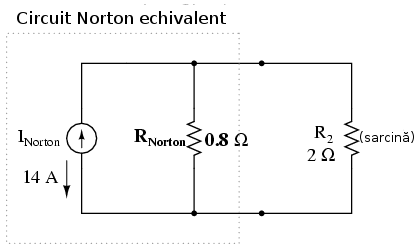
Reconectând rezistenţa de sarcină iniţială (2 Ω), vom analiza circuitul Norton precum o conexiune paralelă simplă:
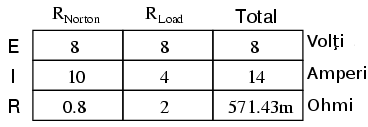
La fel cum am văzut şi în cazul teoremei lui Thevenin, singurele informaţii utile din această analiză sunt valoarea tensiunii şi a curentului prin rezistenţa de sarcină R2; celelalte informaţii cu privire la circuit sunt irelevent. Avantajul constă în simplitatea analizei circuitului atunci când avem mai multe valori ale rezistenţei de sarcină pentru care vrem să aflăm tensiunea şi curentul.
Paşii pentru implementarea teoremei lui Norton:
- Găsirea sursei Norton de curent prin îndepărtarea tuturor rezstorilor din circuitul iniţial şi calcularea curentului prin scurt circuitul creat între punctele de contact ale fostei sarcini a circuitului(scurt circuit)
- Aflarea rezistenţei Norton prin îndepărtarea tuturor surselor de putere din circuit şi calcularea rezistenţei totale dintre punctele de contact ale fostei sarcini a circuitului (circuit descis)
- Realizarea circuitului Norton echivalent, cu sursa de curent şi rezistorul Norton în paralel. Rezistorul de sarcină se re-introduce între cele două puncte deschise ale circuitului echivalent
- Aflarea tensiunii şi curentului prin sarcină aplicând regulile circuitelor paralele
10.9 Echivalenţa teoremelor Thevenin-Norton
Din moment ce ambele teoreme, atât Thevenin cât şi Norton, reprezintă metode valide de reducere a reţelelor complexe spre circuite mult mai simple şi uşor de analizat, trebuie să existe un procedeu de transformare a unui circuit Thevenin echivalent într-unul Norton echivalent.
Metoda de calcuare a rezistenţei este aceeiaşi în ambele cazuri: îndepărtarea tuturor surselor de putere şi determinarea rezistenţei între punctele de conexiune rămase libere. Cele două rezistenţe sunt prin urmare egale:


Luând în considerare faptul că ambele circuite echivalente sunt gândite să se comporte asemenea reţelei originale în ceea ce priveşte alimentarea sarcinii cu tensiune şi curent electric, circuitele Thevenin şi Norton ar trebui şi ele să se comporte identic.
Acest lucru se traduce prin faptul că ambele circuite ar trebui să producă aceeiaşi cădere de tensiune între punctele de contact ale sarcinii, atunci când aceasta nu este prezentă în circuit. Pentru circuitul Thevenin, căderea de tensiune pentru circuitul deschis trebuie să fie egală cu sursa de tensiune Thevenin, 11.2 voţi în acest caz. În cazul circuitului Norton, toţi cei 14 amperi generaţi de sursa de curent trebuie să treacă prin rezistenţa de 0.8 ohmi, producând prin urmare o cădere de tensiune de 11.2 volţi (E=IR). Putem susţine asfel că tensiunea Thevenin este egală cu, curentul Norton înmulţit cu rezistenţa Norton:
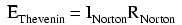
Transformarea unui circuit Norton într-un circuit Thevenin se realizează folosind aceeiaşi valoare a rezistenţei şi calculând tensiunea Thevenin cu ajutorul legii lui Ohm.
În aceeiaşi ordine de idei, atât circuitul Thevenin cât şi circuitul Norton ar trebui să genereze aceeiaşi cantitate de curent printr-un scurt circuit între terminalii sarcinii, atunci când aceasta nu este prezentă în circuit. În circuitul Norton, curentul de scurt circuit este exact curentul sursei (de curent), 14 amperi în acest caz. În circuitul Thevenin, întreaga cădere de tensiune de 11.2 volţi se regăseşte la bornele rezistorului de 0.8 ohmi, ceea ce produce exact acelaşi curent prin scurt (circuit), 14 amperi (I=E/R). Putem susţine asfel că, curentul Norton este egal cu tensiune Thevenin împărţită la rezistenţa Thevenin:
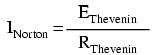
Vom utiliza relaţia de echivalenţă dintre cele două teorema în următoarea secţiune.
10.10 Teorema lui Millman revizuită
Revenim acum asupra teoremei lui Millman pentru a elucida forma „ciudată” a ecuaţiei şi provenienţa acesteia:
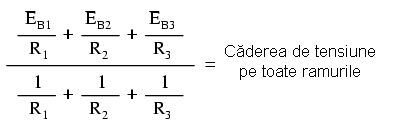
Numitorul ecuaţiei seamănă cu numitorul ecuaţiei pentru calculul rezistenţei paralele, iar termenii E/R ai numărătorului reprezintă valori ale curentului (I=E/R).
Pentru înţelegearea acestei ecuaţii folosim echivalenţa Thevenin-Norton discutată în secţiunea precedentă. Ecuaţia Millman consideră că fiecare ramură reprezintă defapt un circuit Thevenin echivalent; fiecare ramură este apoi transformată într-un circuit Norton echivalent.

În circuitul de mai sus, bateria B1 şi rezistorul R1 sunt văzute ca şi o sursă Thevenin potrivite pentru transformarea într-o sursă Norton de 7 A (28 V / 4 Ω) în paralel cu un rezistor de 4 Ω. Ramura din dreapta se transformă într-o sursă de curent de 7 A (7 V / 1 Ω) şi un rezistor de 1 Ω conectat în paralel. Ramura din centru, neconţinând nicio sursă de tensiune, se transformă într-o sursă de curent Norton de 0 A în paralel cu un rezistor de 2 Ω:
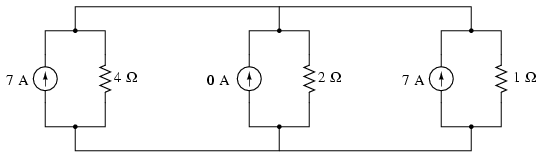
Din moment ce valorile sursele de curent sunt aditive algebric, curentul total prin circuit este de 7 + 0 + 7, adică 14 A. Această adunare a curenţilor surselor Norton este reprezentată la numărătorul ecuaţiei Millman:
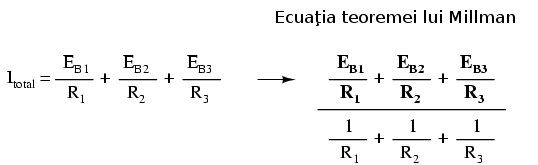
Toate rezistenţele Norton sunt conectate în paralel. Aceast lucru este reprezentat în numitorul ecuaţiei lui Millman:
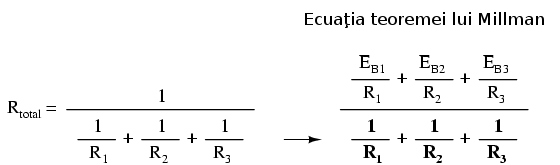
În cazul de faţă, rezistenţa totală este de 517.43 miliohmi (571.43 mΩ). Circuitul echivalent se poate acum redesena şi conţine doar o sursă (de curent) Norton şi o singură rezistenţă Norton:
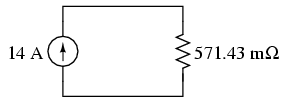
Folosim legea lui Ohm pentru aflarea căderii de tensiune pe aceste două componente (E=IR):
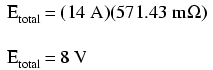
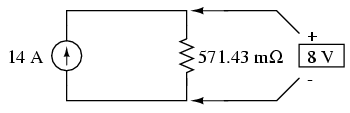
Figure 428: circuit electric
Pe scurt, ştim despre acest circuit că valoarea totală a curentul este dată de suma tuturor tensiunilor pe ramuri împărţite la curenţi lor respectivi. Ştim de asemenea că rezistenţă totală este inversul sumei inversului tuturor rezistenţelor ramurilor. Şi, trebuie să luăm în considerare faptul că putem afla tensiunea totală pe toate ramurile prin înmulţirea curentului total cu rezistenţa totală (E=IR). Tot ce trebuie să facem acum este să punem împreună cele două ecuaţii pentru curentul şi rezistenţa totală, mai exact, putem afla tensiunea totală prin înmulţirea lor:

În acest moment putem realiza faptul că ecuaţia lui Millman nu este nimic altceva decât o transformare Thevenin-Norton împreună cu formula rezistenţei paralele pentru determinarea căderii de tensiune pe toate ramurile circuitului.
10.11 Teorema transferului maxim de putere
Teorema transferului maxim de putere nu este neapărat o metodă de analiza a reţelelor ci este folosită pentru optimizarea design-ului sistemelor. Pe scurt, puterea disipată pe o rezistenţă este maximă atunci când valoarea rezistenţei este egală cu rezistenţa Thevenin/Norton a reţelei de alimentare. Dacă rezistenţa sarcinii este mai mare sau mai mică decât rezistenţa Thevenin/Norton, puterea disipată de aceasta nu va atinge valoarea maximă (eficienţă scăzută).
Acest lucru se urmăreşte în realizarea unui sistem stereo, unei dorim ca „impedanţă” difuzorului să fie aceeiaşi cu „impedanţă” amplificatorului pentru puterea de ieşire (sunet) maximă. Impedanţa este asemănătoare rezistenţei, doar că implică şi efectele curentului alternativ pe lângă cel continuu. O valoare a impedenţei prea mare va rezulta într-o putere de ieşire scăzută. O impedanţă prea mică, pe de altă parte, va rezulta de asemenea într-o putere de ieşire scăzută dar şi într-o posibilă încălzire excesivă a amplificatorului.
Revenind la circuitul studiat până acum…

…conform teoremei transferului maxim de putere, valoarea rezistenţei de sarcină pentru disiparea puterii maxime din circuit, trebuie să fie egală cu rezistenţa Thevenin (0.8 Ω, în acest caz):
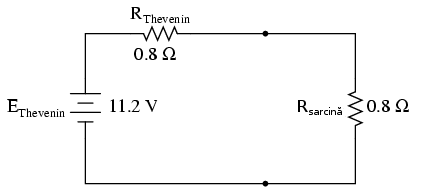
Cu această valoare a rezistenţei, puterea disipată va fi de 39.2 watt:
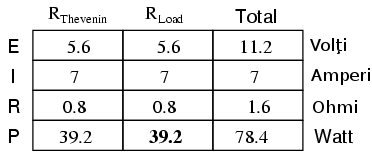
Dacă micşorăm valoarea rezistenţei de sarcină (la 0.5 Ω în loc de 0.8 Ω, de exemplu), puterea disipată pe sarcină descreşte:
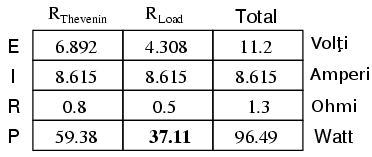
Dacă valoarea rezistenţei sarcinii creşte (la 1.1 Ω în loc de 0.8 Ω, de exemplu), puterea disipată va fi de asemenea mai mică decât valoarea acesteia pentru 0.8 Ω:
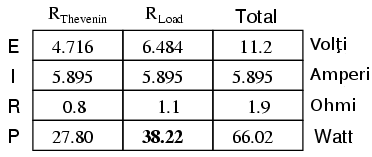
Această teoremă este foarte folositoare atunci când dezoltăm un circuit electric pentru folosirea (disiparea) puterii maxime pe sarcină .
10.12 Transformarea triunghi-stea şi stea-triunghi
De multe ori componentele sunt conectate într-o reţea cu trei terminale, asfel: conexiunea triunghi (Δ) cunoscută şi sub numele de delta sau Pi (π) şi configuraţia stea (Y) cunoscută şi sub numele de T. Ne putem da seama de unde vine numele acestora urmărind desenele de mai jos:
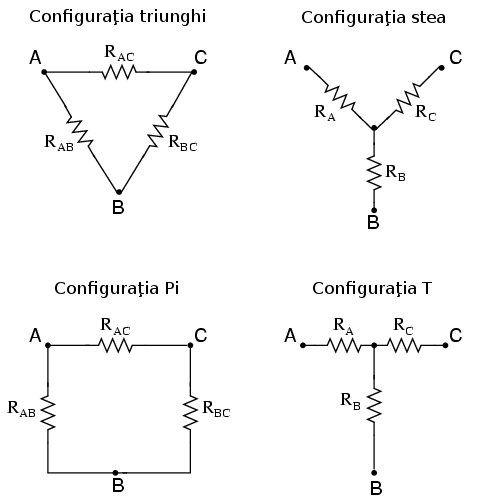
Este posibilă calcularea reală a valorilor rezistorilor necesari pentru formarea unui tip de configuraţie (Δ sau Y) bazându-ne pe valorile rezistorilor celeilalte configuraţii, prin simpla analiză a conexiunilor terminalilor. Pe scurt, dacă avem două reţele de rezistori, una Δ şi una Y, în cadrul cărora rezistorii nu sunt vizibil dar avem la dispoziţie trei terminali (A, B şi C), rezistorii pot fi proiectaţi pentru ambele reţele asfel încât nu am putea face diferenţa dintre cele două reţele din punct de vedere electric. Cu alte cuvinte, configuraţiile echivalente Δ şi Y se comportă identic.
Există câteva ecuaţii pentru transformare unei reţele în celelate:
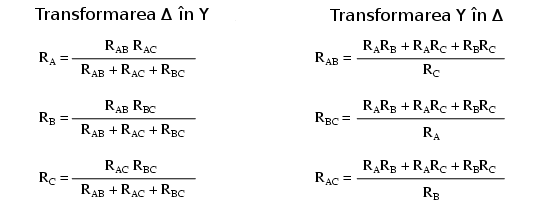
Acest tip de configuraţii sunt frecvent întâlnite în sistemele de putere trifazate de curent alternativ, dar acestea sunt de obicei reţele echilibrate (toţi rezistorii au aceeiaşi valoare) şi prin urmare calculele nu sunt atât de complexe.
Exemplu
O altă aplicaţie a transformării Δ-Y se găseşte în cadrul circuitelor punte dezechilibrate, precum cel de jos:
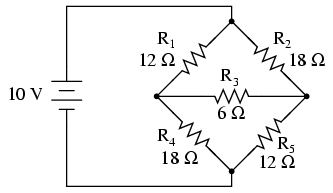
Rezolvarea acestui circuit folosind analiza curentului de ramură sau buclei de curent este destul de laborioasă, iar fiindcă există doar o singură sursă de putere, nici teoremele lui Millman sau superpoziţiei nu ne sunt de prea mare ajutor în acest caz. Putem folosi teorema lui Thevenin sau Norton considerând R3 rezistorul de sarcină, dar le ce ne-ar ajuta?
În schimb, putem considera că rezistorii R1, R2 şi R3 sunt conectaţi în Δ (respectiv Rab, Rac şi Rbc); generăm apoi o reţea Y echivalentă pentru înlocuirea lor şi transformăm prin acest pas puntea într-un circuit combinat (mai simplu) serie/paralel.
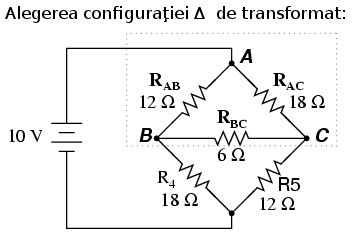
După aplicarea transformării:
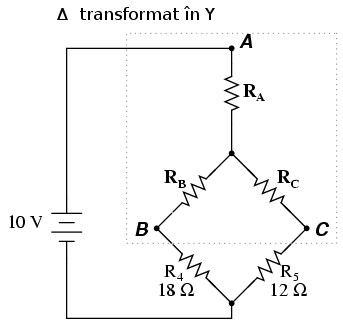
După efectuarea corectă a calculelor, căderile de tensiune între punctele A, B şi C vor fi aceleaşi în ambele circuite
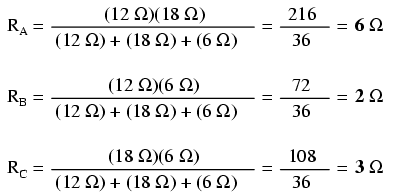
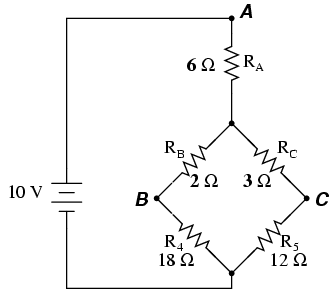
Desigur, valorile rezistorilor R4 şi R5 rămân aceleşi, 18 Ω respectiv 12 Ω. Acum putem analiza circuitul precum o combinaţie serie/paralel, obţinând următoarele rezultate:
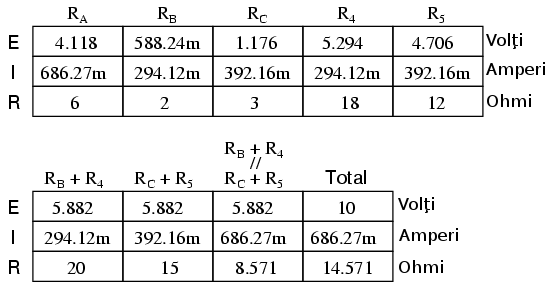
Folosim valorile căderilor de tensiune din tabelul de mai sus pentru determinarea căderilor de tensiune între punctele A, B şi C, fiind atenţi la adunarea sau scăderea lor (precum este cazul tensiunii între punctele B şi C):
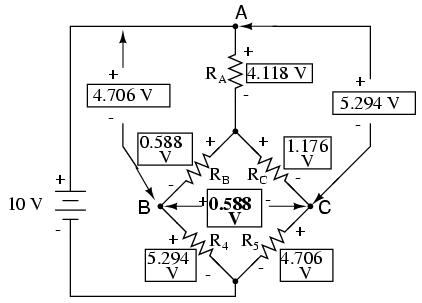
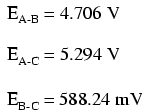
Cu valorile acestor căderi de tensiune aflate, putem trece la circuitul original unde aceste căderi de tensiune sunt aceleaşi (între aceleaşi puncte).
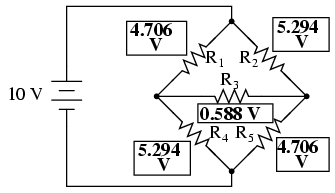
Desigur, căderile de tensiune pe rezistorii R4 şi R5 sunt aceleaşi ca în cazul circuitului transformat (Y).
Acum putem determina curenţii prin rezistori folosind valorile acestor tensiuni şi aplicând repetat legea lui Ohm (I=E/R):