< Curent continuu
8 Aparate de masura electrice
8.1 Ce este un aparat de măsură
Un aparat de măsură este orice dispozitiv special realizat pentru afişarea unei mărimi electrice într-un format ce poate fi interpretat de către un operator uman. De obicei, acest format este sub formă vizuală: deplasarea unui indicator pe o scală, o serie de dispozitive luminoase aranjate sub forma unui bargraph, sau un afişaz format din cifre. În analiza şi testarea circuitelor, există dispozitive proiectate pentru realizarea măsurătorilor mărimilor electrice de bază, şi anume, tensiune, curent şi rezistenţa. Există multe alte tipuri de aparate de măsură, dar în acest capitol ne vom concentra atenţia, în principal, pe modul de funcţionare al acestora trei.
Majoritatea aparatelor de măsură moderne sunt digitale, folosind un afişaj numeric. Modelele mai vechi de aparate de măsură sunt însă mecanice, utilizând un indicator pentru afişarea mărimii măsurate. În ambele cazuri, este nevoie de o setare a aparatului pentru indicarea corespunzătoare a mărimilor măsurate. În acest capitol ne vom referi exclusiv asupra principiilor de funcţionare ale aparatelor de măsură analogice (mecanice).
8.1.1 Principiul aparatelor de măsură electromagnetice
Majoritatea aparatelor de măsură analogice se bazează pe principiul electromagnetismului, şi anume, pe faptul că trecerea unui curent printr-un conductor produce un câmp magnetic perpendicular pe axa de deplasare a electronilor. Cu cât valoarea curentului este mai mare, cu atât mai mare va fi câmpul magnetic produs. Dacă acest câmp magnetic produs de conductor este liber să interacţioneze cu un alt câmp magnetic, vom asista la dezvoltarea unei forţe fizice între cele două surse ale câmpurilor magnetice. Dacă una dintre acest surse este liberă să se deplaseze faţă de cealaltă sursă, aceasta se va deplasa pe măsură ce curentul trece prin conductor, deplasarea fiind direct proporţională cu mărimea curentului.
8.1.2 Galvanometrul

Primele astfel de aparate de măsură construite erau cunoscute sub numele de galvanometre, fiind recunoscute pentru precizia lor. Un model foarte simplu de galvanometru constă dintr-un ac magnetizat (asemenea celui folosit la compas) suspendat la capătul unui fir şi poziţionat în interiorul unei înfăşurări conductoare. La trecerea curentului prin acest colac, se va produce un câmp magnetic ce va modifica poziţia iniţială a acului. Un astfel de aparat antic este prezentat în figura alăturată.
Astfel de aparate nu mai sunt însă practice în prezent, fiind extrem de sensibile la orice tip de mişcare şi la interferenţele datorate câmpului magnetic al pământului. Singurul lor scop rămâne prezentarea conceptelor de bază ale dispozitivelor expermentale. În prezent, termenul de „galvanometru” este utilizat pentru desemnarea oricărui tip de aparat de măsură de o prezicie excepţională nereprezetând neapărat un astfel de dispozitiv prezentat mai sus.
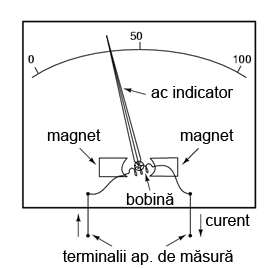
Aparatele de măsură electromagnetice sunt realizate în prezent dintr-o bobină suspendată într-un câmp magnetic, protejată de majoritatea influenţelor externe. Astfel de dispozitive sunt cunoscute sub numele de aparate de măsură cu magnet permanent.
În figura de mai sus, acul indicator este poziţionat aproximativ la 35% pe scala valorilor, zero fiind în stânga iar valoarea maximă regăsindu-se în partea dreaptă. O creştere a curentului de măsurat va duce la o deplasare a acului indicator spre dreapta iar o descreştere a lui va duce la o deplasare a acului spre stânga. Afişajul aparatului de măsură conţine o scală gradată cu cifre pentru indicarea valorilor mărimii de măsurat, indiferent de tipul acesteia. Cu alte cuvinte, dacă este necesară o valoare de 50 µA pentru deplasarea maximă a acului indicator (spre capătul din dreapta), scala va avea scrisă o valoarea de 0 µA în partea stângă şi o valoare de 50 µA în partea dreaptă; mijlocul va fi desigur 25 µA. În exemplul din figură, acul ar indica în acest caz ipotetic o valoare a curentului de 17,5 µA. De obicei, scala este împărţită în gradaţii mult mai mici, din 5 în 5 µA, sau chiar la 1 µA, pentru a permite o citire mult mai precisă a indicaţiei acului.
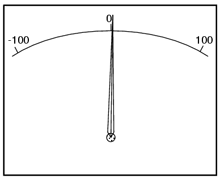
Majoritatea aparatelor pot detecta polaritatea curentului, o direcţie a acestuia ducând la deplasarea acului într-un anumit sens, iar direcţia opusă a curentului ducând la o deplasare în sens contrar al acului indicator. Modele D'Arsonval şi Weston sunt de acest tip.
Există însă şi aparate care nu sunt sensibile la modificarea sensului curentului prin circuit, bazându-se pe atragerea unui cursor mobil de fier, nemagnetizat, către conductorul de curent fix pentru deplasarea acului inducator. Astfel de aparate sunt folosite pentru măsurător în curent alternativ. Un dispozitiv sensibil la variaţia polarităţii curentului, ar vibra pur şi simplu înainte şi înapoi fără a putea da o indicaţie practică a mărimii de măsurat.
8.1.3 Aparate de măsură electrostatice
Deşi majoritatea aparatelor de măsură analogice se bazează pe principiul electromagnetismului, câteva dintre ele se bazează pe electrostatică, cu alte cuvinte, pe forţa de atracţie sau de respingere generată de sarcinile electrice în mediul dintre ele.
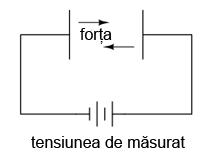
Dacă aplicăm o tensiune între două suprafeţe conductoare separate printr-un dielectric format din aer, va exista o forţă fizică de atracţie dintre cele două suprafeţe, forţa capabilă să deplaseze un mecanism de măsurare. Această forţă este direct proporţională cu tensiunea aplicată între plăci şi invers proporţională cu pătratul dinstanţei dintre ele. De asemenea, forţa nu depinde de polaritate, rezultând astfel un dispozitiv insensibil la variaţia polarităţii tensiunii.
Din păcate, forţa generată de atracţia electrostatică este foarte mică în cazul tensiunilor normale, astfel încât aceste tipuri de aparate de măsură nu sunt practice pentru instrumentele de test normale. Astfel de aparate electrostatice sunt folosite pentru măsurarea tensiunilor înalte, de ordinul miilor de volţi. Unul dintre cele mai mare avantaje al aparatelor electrostatice constă în rezistenţa electrică extrem de mare, fată de aparatele electromagnetice care au o rezistenţa electrică mult mai mică. După cum vom vedea în cele ce urmează, o rezistenţa electrică mare, rezultând într-un curent mult mai mic prin dispozitiv, este absolut necesară pentru realizarea unui voltmetru profesional.
Tubul catodic (CRT)
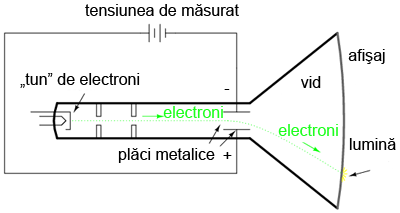
O aplicaţie mult mai întâlnită a dispozitivelor electrostatice este tubul catodic. Acestea sunt tuburi speciale din sticlă, similare celor întâlnite la televizoarele clasice. Într-un astfel de tub, un fascicol de electroni ce se deplasează prin vid, este deviat prin intermediul unei tensiuni existente între două plăci metalice aşezate de o parte şi de cealaltă a tubului. Datorită faptului că electronii posedă o sarcină electrică negativă, aceştia tind să fie respinşi de placa negativă şi atraşi de placa pozitivă. O inversare a polarităţii ensiunii dintre cele două plăci va duce la modificarea în sens contrar al traseului fascicolului de electroni, acest dispozitiv fiind prin urmare sensibil la polaritate.
Electronii, având o greutate mult mai mică decât plăcile metalice, deplasează mult mai uşor sub acţiunea forţei dintre cele două plăci decât plăcile propriu-zise. Traseul lor deviat poate fi detectat pe măsură ce aceştia se lovesc de afişajul din sticla de la capătul tubului, unde întâlnesc un strat subţire de fosfor; rezultatul este emiterea unei unde luminoase ce poate fi observată din exteriorul tubului. Cu cât tensiunea dintre cele două plăci este mai mare, cu atât electronii vor fi deviaţi mai puteric de la traseul lor iniţial, punctul luminos de pe afişaj regăsindu-se la o distanţa mai mare faţă de centrul acestuia.

Un astfel de tub este prezentat în figura alăturată. Într-un tub real, precum cel alăturat, există două perechi de placi metalice pentru deviaţia electronilor, nu doar una singură, pentru a putea acoperi întreaga aria a afişajului de sticlă din capătul dispozitivului.
Cu toate că acest dispozitive pot înregistra tensiuni mică cu o precizie ridicată, ele sunt totuşi greoaie, fragile şi necesită putere electrică pentru funcţionare, spre deosebire de dispozitivele electromagnetice ce sunt mult mai compacte şi sunt alimentate direct de semnalul de măsurat ce se regăseşte la bornele lor. De obicei, tuburile catodice sunt folosite în combinaţie cu circuite externe precise pentru formarea unui echipament de test mult mai mare, şi anume, osciloscopul. Acest din urmă dispozitiv poate indica variaţia tensiunii cu timpul, o abilitatea extrem de importantă în cazul circuitelor cu tensiuni şi curenţi variabili în timp.
8.2 Voltmetrul
Majoritatea aparatelor de măsură sunt dispozitive foarte sensibile. Unele modele, precum D'Arsonval, necesită un curent de doar 50 µA pentru a duce acul indicator în poziţia maximă a scalei de valori; rezistenţa internă a acestor tipuri de aparate nu este mai mare de 1000 Ω. În consecinţă, un astfel de voltmetru poată măsura o tensiune maximă de doar 50 mV (50 µA X 1000 Ω), pentru că la această valoare, acul indicator este în poziţia sa maximă (dreapta) şi nu se mai poate deplasa. Pentru a putea realiza voltmetre practice, cu capabilităţi de măsurare a unor tensiuni mult mai mari, folosind aceste dispozitive sensibile, trebuie găsită o metodă de reducere a deplasării acului indicator.
8.2.1 Modelul D'Arsonval
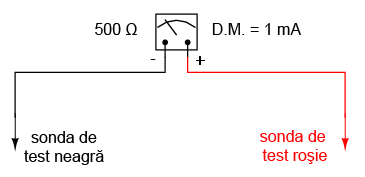
Să luăm ca şi prim exemplu un dispozitiv tip D'Arsonval, cu o rezistenţa internă a bobinei de 500 Ω, şi a cărei deplasare maximă (D.M.) se realizează pentru un curent de 1 mA.
Aplicând legea lui Ohm, putem determina tensiunea necesară deplasării acului indicator la valoarea maximă:
E = IR E = (1 mA)(500 Ω) E = 0,5 V
Dacă am dori să folosim acest aparat pentru măsurarea tensiunilor ce nu depăşesc o jumătate de volt, această configuraţie ar fi mai mult decât suficientă. Dar pentru a măsură tensiuni peste această valoare, trebuie să aducem unele modificări. Pentru a obţine o deplasare observabilă a acului pentru o valoare a tensiunii de peste 0,5 V, este nevoie ca doar o parte din tensiune de măsurat să se regăsească pe bobina internă. Desigur, va trebui să modificăm şi scala aparatului de măsură, astfel încât să existe o legătură directă între deplasarea acului indicator şi valoarea reală a tensiuni măsurate.
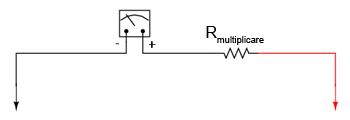
Această operaţie se poate realiza foarte uşor cu ajutorul unui divizor de tensiune. Ştiind că un divizor de tensiune se realizează cu ajutorul rezistorilor conectaţi în serie, tot ceea e trebuie să facem este să conectăm un rezistor în serie cu rezistenţa internă a configuraţiei iniţiale (înclusă în dispozitiv), rezultatul fiind un divizor de tensiune format din doi rezistori.
Rezistorul serie poartă numele de „rezistor de multiplicare” datorită faptului că multiplică valoare tensiunii ce poate fi măsurată. Determinarea valorii rezistenţei este uşoară dacă suntem familiarizaţi cu analiza circuitelor serie. De exemplu, să determinăm valoarea Rmultiplicare pentru ca dispozitivul de mai sus (1 mA, 500 Ω) să poată măsura tensiuni de până la 10 V.
| Unitate | Deplasare | Rmultiplicare | Total | Unitate |
|---|---|---|---|---|
| E | V | |||
| I | A | |||
| R | Ω |
Putem folosi metoda tabelului pentru a ne uşura calculele.
| Unitate | Deplasare | Rmultiplicare | Total | Unitate |
|---|---|---|---|---|
| E | 10 | V | ||
| I | 1 m | 1 m | 1 m | A |
| R | 500 | Ω |
Cunoscând faptul că deplasarea va fi maximă pentru un curent de 1 mA, precum şi faptul că tensiunea la care dorim ca acest lucru să se întâmple este de 10 V (circuit serie, valoare totală), putem completa tabelul astfel.
| Unitate | Deplasare | Rmultiplicare | Total | Unitate |
|---|---|---|---|---|
| E | 10 | V | ||
| I | 1 m | 1 m | 1 m | A |
| R | 500 | 9,5 k | 10 k | Ω |
Există mai multe metode de determinare a rezistenţei de multiplicare. O variantă presupune determinarea rezistenţei totale a circuitului aplicând legea lui Ohm pe coloana „total” (R = E / I), scazând apoi valoarea de 500 Ω a deplasării pentru a obţine valoarea Rmultiplicare. O a doua metodă constă în determinarea căderii de tensiune pe rezistenţa internă atunci când deplasarea acului indicator este maximă (E = IR), căderea de tensiunea pe rezistorul de multiplicare fiind egală cu diferenţa dintre căderea de tensiune totală şi căderea de tensiune pe rezistenţa internă.
| Unitate | Deplasare | Rmultiplicare | Total | Unitate |
|---|---|---|---|---|
| E | 0,5 | 9,5 | 10 | V |
| I | 1 m | 1 m | 1 m | A |
| R | 500 | 9,5 k | 10 k | Ω |
Ultimul pas constă în aplicarea legii lui Ohm (R = E / I) pentru determinarea rezistenţei rezistorului de multiplicare.
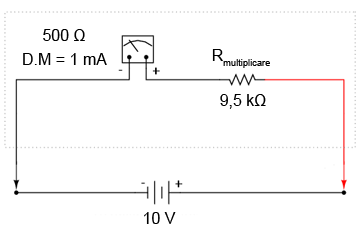
Indiferent de metoda folosită, răspunsul final este acelaşi (9.5 kΩ). Putem aplica ambele metode, pentru a ne asigura că rezultatul final este corect.
Cu o cădere de tensiune de exact 10 V între terminalii aparatului de măsură, curentul prin bobina internă va fi de exact 1 mA, acest curent fiind limitat de rezistorul de multiplicare şi de rezistenţa internă a bobinei. Căderea de tensiune pe bobină va fi de exact 0,5 V, iar deplasarea acului indicator va fi maximă (spre dreapta). Dacă am modificat şi scala astfel încât valorile acesteia să fie cuprinse între 0 şi 10 V (în loc de 0 şi 1 mA), orice persoană care va citi indicaţia aparatului o va interpreta ca fiind 10 V. Nu este necesar ca utilizatorii voltmetrului să cunoscă faptul că aparatul foloseşte doar o fracţiune din tensiunea totală de măsurat (10 V) a sursei externe. Tot ceea ce contează este ca circuitul să funcţioneze corect pentru a putea indica tensiunea totală aplicată.
Acesta este într-adevăr şi modul de realizare şi utilizare al aparatelor de măsură: dispozitivul de detectare al mărimii de măsurat este construit astfel încât să fie necesară doar o cantitate foarte mică de tensiune şi de curent pentru funcţionarea acestuia, pentru o sensibilitatea cât mai ridicată. Această configuraţie este apoi conectată la un circuit divizor realizat cu rezistori de prezizie, pentru a putea indica o tensiune sau un curent mult mai mari.
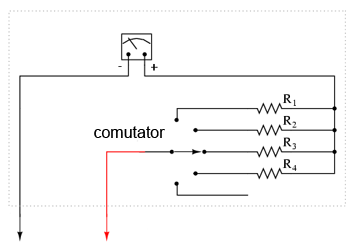
În general, este foarte utilă prezenţa mai multor astfel de circuite divizoare, pentru a putea măsură o plajă destul de largă de valori folosind acelaşi mecanism de bază pentru detectarea semnalului. Acest lucru se poate realiza printr-un comutator multi-polar şi câţiva rezistori de multiplicare, fiecare pentru o anumită bandă de tensiuni, conform figurii alăturate.
Comutatorul cu cinci poziţii intră în contact doar cu cât un rezistor deodată. În poziţia de jos, acesta nu face contact cu niciun rezistor, fiind de fapt în poziţia „oprit”. Fiecare rezistor realizează o deplasare maximă diferită a voltmetrului, şi toate se bazează pe aceleaşi caracteristici principale (1 mA, 500 Ω).
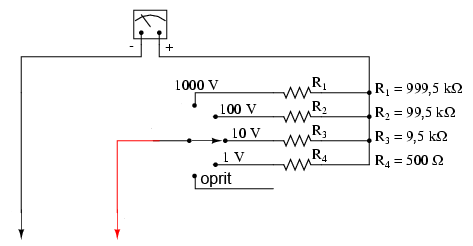
Cu o astfel de variantă, valoarea fiecărui rezistor este determinată folosind aceiaşi metodă utilizată mai sus, cunoscând tensiunea totală necesară în fiecare caz. Pentru un volmetru cu scala tensiunilro de 1 V, 10 V, 100 V şi 1000 V, rezistenţele de multiplicare sunt conform figurii alăturate.
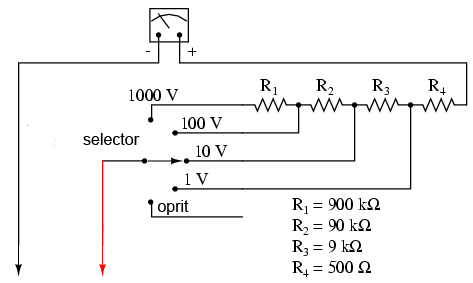
Putem observa că valorile rezistorilor de multiplicare sunt puţin ciudate. Este puţin probabil să găsim un rezistor de precizie cu o valoare de 999,5 kΩ, astfel încât suntem nevoiţi să folosim o altă configuraţie.
Cu fiecare pas, tot mai mulţi rezistori sunt conectaţi în circuit prin intermediul comutatorului (selectorului), astfel că rezistenţa totală este va fi egală cu suma rezistenţelor individuale. De exemplu, atunci când comutatorul se află în poziţia „1000 V”, ştim din exemplu precedent că avem nevoie de o rezistenţă de 999,5 kΩ. Folosind configuraţia anterioară, aceasta este exact valoarea obţinută:
Rtotal = R1 + R2 + R3 + R4 Rtotal = 900 kΩ + 90 kΩ + 9 kΩ + 500 kΩ Rtotal = 999,5 kΩ
Avantajul constă, desigur, în faptul că rezistorii de 900 kΩ, 90 kΩ şi 9 kΩ sunt mult mai uşor de procurat decât cei precedenţi (999,5 kΩ, 99,5 kΩ şi 9,5 kΩ). Din punct de vedere funcţional, nu există nicio diferenţa între cele două configuraţii prezentate.
8.3 Impactul voltmetrului asupra circuitului
Orice aparat de măsură introdus în circuit modifică comportamentul acestuia din urmă într-o oarecare măsură. Deşi impactul este inevitabil, acesta poate fi minimizat printr-o proiectare bună a aparatului de măsură în cauză.
Din moment ce voltmetrele se conectează tot timpul în paralel cu componentul sau componentele aflate sub test, orice curent prin voltmetru va modifica curentul total din circuitul de măsurat, ducând inevitabil şi la modificarea tensiunii reale din circuit. Un voltmetru ideal posedă o rezistenţă internă infinita, astfel încât curentul care trece prin acesta să fie de 0 A pentru a nu afecta circuitul testat. Totuşi, astfel de voltmetre nu există decât în paginile cărţilor, nu şi în viaţa reală!
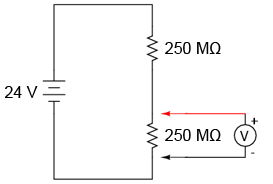
Să luăm ca şi exemplu circuitul divizor de tensiune din figura alăturată, ca şi un exemplu extrem al efectelor unui voltmetru asupra circuitului de măsurat.
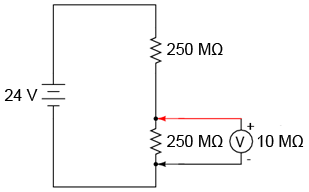
Atunci când voltmetrul nu este conectat în circuit, vom aveam o cădere de tensiune de exact 12 V pe fiecare dintre cei doi rezistori (vezi circuitele divizoare de tensiune). Totuşi, dacă voltmetrul considerat în acest exemplu posedă o rezistenţa internă între cele două sonde de 10 MΩ (o valoare normală pentru un voltmetru digital), aceasta va crea un subcircuit paralel cu rezistorul inferior al divizorului.
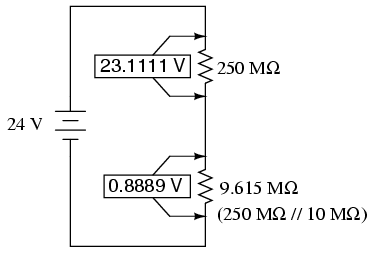
Acest lucru duce la scăderea rezistenţei inferioare de la 250 MΩ la 9,61 MΩ (circuit paralel), modificând fundamental căderile de tensiune din circuit.
Un divizor de tensiune cu rezistenţele de 250 MΩ, respectiv 9,61 MΩ va diviza o tensiune de 24 V în 23,11 V, respectiv 0,88 V. Din moment ce voltmetrul face parte din rezistenţa de 9,61 MΩ, aceasta este şi valoarea pe care o va indica: 0,88 V.
Voltmetrul poate indica doar căderea de tensiune dintre punctele în care este conectat. Acesta nu poate „ştii” că înainte de introducerea sa în circuit, în acea locaţie exista o cădere de tensiune de 12 V şi nu de 0,88 V. Conectarea aparatului de măsură în circuit modifică rezistenţa circuitului şi prin urmare şi valoarea căderii de tensiune măsurate, aceasta nefiind prin urmare cea reală.
Acest efect este prezent, într-o anumită măsură, ori de câte ori folosim un voltmetru. Scenariul prezentat mai sus este unul extrem, cu o rezistenţa a voltmetrului mult mai mică decât rezistenţa divizorului de tensiune. Din aceste motive, cu cât rezistenţa internă a voltmetrului este mai mare, cu atât efectul acestuia asupra circuitului de măsurat va fi mai mic. Din această cauză, un voltmetru ideal posedă o rezistenţă infinită. Dar, indiferent de valoarea acestei rezistenţe, efectul prezentat mai sus va fi tot timpul prezent într-un circuit.
8.3.1 Sensibilitatea voltmetrelor
Impactul creat de voltmetrele electromecanice asupra circuitelor este desemnat prin numărul de ohmi prezenţi între terminalii aparatului pentru fiecare domeniu de tensiune (poziţii diferite ale selectorului). Practic, acesta este un număr exprimat în Ω/V. Voltmetrele digitale posedă de obicei o rezistenţa constantă între sondele aparatului indiferent de domeniu de tensiune ales.

Să reluăm exemplu din secţiunea precedentă. Pe domeniul 1000 V, rezistenţa totală este de 1 MΩ (999,5 kΩ + 500Ω), ceea ce înseamnă 1 MΩ / 1000 V, sau 1 kΩ/V. Această sensibilitate rămâne constantă indiferent de domeniul ales:
domeniul 100 V; sensibilitatea: 100 kΩ / 100 V = 1 kΩ / V domeniul 10 V; sensibilitatea: 10 kΩ / 10 V = 1 kΩ / V domeniul 1 V; sensibilitatea: 1 kΩ / 1 V = 1 kΩ / V
Astfel, valoarea exprimată în ohm/volt este o caracteristică principală a voltmetrului, şi nu depinde de domeniul selectat. Dacă suntem foarte atenţi, putem observa că această valoare este determinată de un singur factor: curentul necesar pentru deplasarea maximă a acului indicator, în acest caz, 1 mA. „Ohm/volt” este inversa matematică a raportului „volt/ohm”, ceea ce conform legii lui Ohm, este chiar curentul (I = E / R). Prin urmare, curentul necesar deplasării maxime dictează sensibilitatea ohm/volt a aparatului, indiferent de domeniile de tensiune disponibile şi de valorile rezistorilor de multiplicare. În cazul nostru particular, o deplasare maximă pentru valoarea de 1 mA rezultă într-o sensibilitate de 1000 Ω/V, indiferent de modul de aranjare al rezistorilor de multiplicare.
Pentru minimizarea efectelor asupra circuitelor, curentul de deplasare maximă trebuie să fie prin urmare cât mai mic. Acest lucru se poate realiza prin reproiectarea aparatului pentru o sensibilitatea maximă (un curent mai mic pentru o deflecţie maximă). Variabila ce trebuie luată însă în considerarea este robusteţea aparatului: cu cât deplasarea este mai sensibilită, cu cât acesta tinde să fie mai fragil.
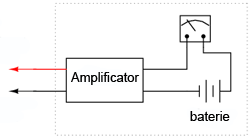
O altă modalitate constă în amplificarea electronică a curentului necesar deplasării, astfel încât curentul ce este absorbit de către aparat din circuit să fie cât mai mic. Acest tip de circuit electronic poartă numele de amplificator.
Nu vom intra în detaliile modului de funcţionare ala amplificatorului aici, dar putem spune că circuitul permite tensiuni de măsurat sa controleze valoarea curentului prin ampermetru. Astfel, curentul necesar deplasării acului indicator este generat de o baterie internă şi nu de circuitul exterior. Şi în acest caz există un anumit curent absorbit de aparat din circuitul măsurat, dar acesta este de sute sau mii de ori mai mici decât curentul absorbit în mod normal de un astfel de aparat fară amplificare.
8.3.2 Detectorul de nul
O ultimă soluţie, şi una foarte ingenioasă, la problema efectului introdus de voltmetru în circuit, îl constitue detectorul de nul. Acesta nu necesită un circuit complicat, dar este nevoie de multă pricepere din partea utilizatorului.
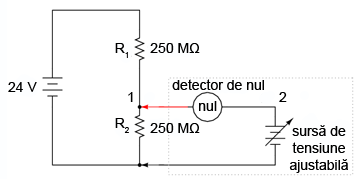
Într-un detector de nul, o sursă de tensiune de precizie, ajustabilă, este comparată cu tensiune de măsură iar aparatul indică diferenţa de tensiune dintre cele două. În cazul în care indicaţie este zero (nulă), căderea de tensiune din circuitul de test este egală cu tensiunea sursei de tensiune de precizie, iar curentul absorbit din circuit va fi de zero amperi. În unele situaţii, aparatul este prevăzut cu un potenţiometru de precizie pentru reglarea fină a tensiunii.
Deoarece scopul unui detector de nul este indicarea precisă a condiţiei de zero (volţi), şi nu indicarea unei valori specifice diferite de zero, scala de valori folosită este irelevantă. Aceste dispozitive sunt proiectate a fi cât mai sensibile cu putinţă.
Un detector de nul extrem de simplu constă dintr-un set de căşti, utilizând difuzoarele pe post de „ac indicator”. Dacă amplicăm o tensiune de c.c. unui difuzor, curentul rezultat va deplasa conul acestuia, iar difuzorul va produce un „click” scurt. Un alt „click” se poate auzi la deconectarea sursei de c.c.
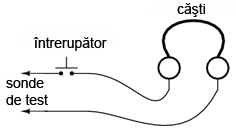
Luând în considerare acest principiu, un detector de nul sensibil poate fi realizat dintr-o simplă pereche de căşti şi un întrerupător.
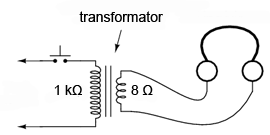
Dacă folosim o pereche de căşti de 8 Ω, sensibilitatea aparatului poate fi crescută prin conectarea sa la un transformator coborâtor de tensiune. La închidere/deschiderea întrerupătorului, curentul mic de la intrare va avea o valoare mult mai mare la ieşirea transformatorului. Rezultatul este un „click” mai puternic şi mai uşor de sesizat, chiar şi pentru curenţi mult mai mici.
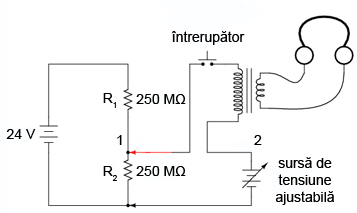
Conectat în circuitul cu detector de nul prezentat mai sus, configuraţia arată precum în figura alăturată.
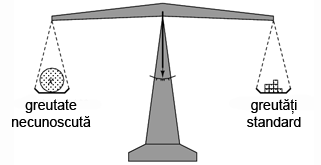
Scopul oricărui detector de nul este să se comporte precum o balanţă de laborator, indicând condiţia de egalitate ale celor două tensiuni, sau, altfel spus, lipsa unei căderi de tensiune între cele două puncte (1 şi 2). O astfel de balanţă nu măsoară de fapt nimic, ci doar indică egalitatea între o greutate necunoscută şi un set de greutăţi calibrate standard.
Asemănător, detectorul de nul indică pur şi simplu momentul în care căderea de tensiune între punctele 1 şi 2 este egală (potenţialul celor două puncte este egal). Conform legii lui Kirchhoff pentru tensiune, acest lucru se va întâmpla atunci când sursa de tensiune ajustabilă este egală cu căderea de tensiune pe rezistorul R2.
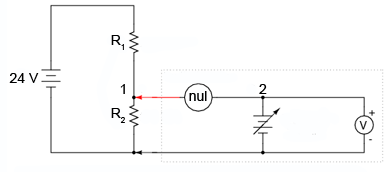
Pentru a utiliza acest instrument, trebuie să ajustăm manual sursa de tensiune prin intermediul unui potenţiometru, acţionând de fiecare data întrerupătorul, până în momentul în care detectorul de nul va indica o condiţie de zero. Circuitul este echilibrat atunci când, în urma acţionării întrerupătorului, nu se va mai auzi nici un sunet la căşti. Valoarea căderii de tensiune pe R2 va fi citită de pe un volmetru conectat la sursa de tensiune de precizie.
Voltmetrul utilizat la bornele sursei de tensiune de prezicie nu trebuie neapărat sa aibă o sensibilitate Ω/V foarte ridicată, deoarece curentul necesar funcţionăii acestuia va fi generat de către sursă. Atâta timp cât căderea de tensiune pe detectorul de nul este zero, nu va exista niciun curent între punctele 1 şi 2, impactul voltmetrului asupra circuitului fiind inexistent.
Merită să reamintim faptul că această metodă, executată perfect, aproape că nu introduce nicio rezistenţă suplimentară în circuitul de măsurat. Ideal, această rezistenţa ar fi zero, dar pentru atingerea acestui scop, căderea de tensiune pe detectorul de nul ar trebui să fie exact zero volţi. Acest lucru ar fi posibil doar prin intermediul unei metode de detectarea infinit sensibile şi o tensiune la fel de precisă din partea surse de tensiune de precizie. Totuşi, în ciuda acestui „neajuns”, un astfel de circuit reprezintă o metodă excelentă de măsurare a căderilor de tensiune. Şi, comparată cu soluţia amplificatorului, ce rezolvă această problemă cu ajutorul tehnologiei avansate, soluţia de faţă rezolvă problema aproape perfect utilizând o lege fundamentală a circuitelor electrice (legea lui Kirchhoff pentru tensiune).
8.4 Ampermetrul
Un aparat de măsură conceput special pentru măsurarea valorii curentului electric (în amperi), poartă numele de ampermetru.
La proiectarea ampermetrelor, rezistorii de multiplicare (rezistori de şunt în acest caz) se vor conecta în paralel şi nu în serie, precum era cazul voltmetrelor. Asta datorită faptului că dorim o divizare a curentului, nu a tensiunii, iar un divizor de curent se realizează prin rezistori conectaţi în serie.
Considerând aceiaşi deplasare precum în cazul voltmetrului, putem observa că un astfel de aparat este destul de limitat, deplasarea maximă realizându-se pentru un curent de doar 1 mA.

Odată cu extinderea plajei de valori ale aparatului de măsură, trebuie să modificăm şi scala valorilor pentru a reflecta această modificare. De exemplu, pentru un ampermetru a cărei valoare maximă măsurată poate atinge 5 A, deplasarea indicatorului fiind aceiaşi, va trebui să modificăm marcajul astfel: 0 A în partea stângă şi 5 A în partea dreaptă, în loc de 0 mA şi 1 mA.
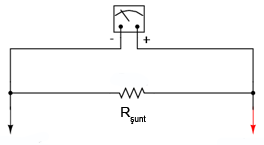
După ce ne-am hotărât ca vrem să extindem domeniul maxim la 5 A, vom trece la determinarea rezistenţei de şuntare. Aceasta va asigura o valoare maximă a curentului prin dispozitivul de detectare propriu-zis de maxim 1 mA şi nu de 5 A (în situaţia în care curentul printre cele două sonde nu depăşeşte nici el valoarea de 5 A).
| Unitate | Deplasare | Rşunt | Total | Unitate |
|---|---|---|---|---|
| E | V | |||
| I | 1 m | 5 | A | |
| R | 500 | Ω |
Putem introduce datele cunoscute într-un tabel, pentru uşurarea calculelor.
| Unitate | Deplasare | Rşunt | Total | Unitate |
|---|---|---|---|---|
| E | 0,5 | V | ||
| I | 1 m | 5 | A | |
| R | 500 | Ω |
Din valorile cunoscute, putem determina căderea de tensiune pe aparatul de măsură, aplicând legea lui Ohm (E = IR).
| Unitate | Deplasare | Rşunt | Total | Unitate |
|---|---|---|---|---|
| E | 0,5 | 0,5 | 0,5 | V |
| I | 1 m | 5 | A | |
| R | 500 | Ω |
Circuitul de faţă este un circuit paralel, prin urmare, căderile de tensiune pe şunt, pe sistemul de detectare a deplasarării, precum şi între cele două sonde ale aparatului de măsură, trebuie să fie egale.
| Unitate | Deplasare | Rşunt | Total | Unitate |
|---|---|---|---|---|
| E | 0,5 | 0,5 | 0,5 | V |
| I | 1 m | 4,99 | 5 | A |
| R | 500 | Ω |
Ştim de asemenea ca prin şunt, curentul trebuie să fie egal cu diferenţa dintre curentul total (5 A) şi curentul deplasării (1 mA), datorită adunării curenţilor de ramuri în configuraţia parelel.
| Unitate | Deplasare | Rşunt | Total | Unitate |
|---|---|---|---|---|
| E | 0,5 | 0,5 | 0,5 | V |
| I | 1 m | 4,99 | 5 | A |
| R | 500 | 100,02 m | Ω |
Aplicând apoi legea lui Ohm (R = E / I), determinăm rezistenţa de şunt necesară.
Desigur, în realitate, rezistenţa de şunt se regăşeste în interiorul aparatului de măsură.
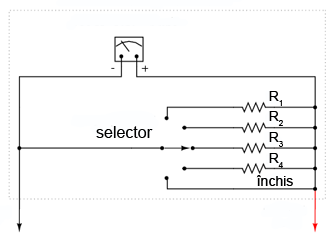
La fel ca şi în cazul voltmetrelor, pot exista mai multe valori ale curenţilor de deplasare maximă. Acest lucru se realizează prin introducerea în circuit a unui număr suplimentar de rezistori de şunt. Selectarea lor se realizează printr-un comutator (selector) multi-polar.
Observăm că rezistorii sunt conectaţi în paralel cu aparatul de măsură, şi nu în serie precum în cazul voltmetrului. Selectorul cu cinci poziţii realizează contact doar cu câte un rezistor pe rând. Marimea fiecărui rezistor este diferită şi conform cu deplasarea maximă a domeniului respectiv de valori, bazându-se pe caracteristicile sistemului de detectare al deplasării (1 mA, 500 Ω).
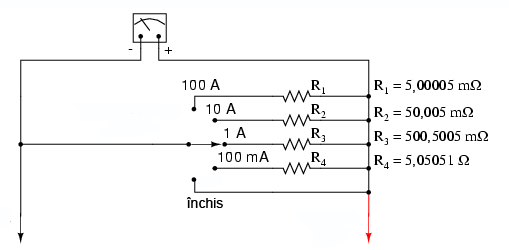
Valoarea fiecărui rezistor se determină prin aceiaşi metodă, luând în considerare curentul total, deplasarea maximă şi rezistenţa internă. Pentru un ampermetru cu un domeniu de valori maxim de 100 mA, 1 A, 10 A, respectiv 100A, rezistenţele de şunt sunt conform figurii alăturate.
Aceste rezistenţe de şunt sunt extrem de mici! Pentru a atinge astfel de rezistenţe, rezistori de şunt ai ampermetrelor trebuie realizaţi de cele mai multe ori printr-o comandă specială din conductori cu diametru relativ mare sau din plăci metalice solide.
Trebuie să fim atenţi însă la puterea disipată în această situaţie. Faţă de voltmetru, curentul prin rezistorii unui ampermetru sunt destul de mari. Dacă acei rezistori nu sunt proiectaţi corespunzător, se pot încălzi şi distruge, sau, în cel mai „fericit” caz, îşi pot pierde acurateţea prin încălzire excesivă. Pentru exemplul precedent, puterea disipată pentru valoarea maximă a deplasării, în valori aproximative, este următoarea:
PR1 = E2 / R1 = (0,5 V)2 / 5,00005 mΩ = 50 W PR2 = E2 / R2 = (0,5 V)2 / 50,005 mΩ = 5 W PR3 = E2 / R3 = (0,5 V)2 / 500,5 mΩ = 0,5 W PR4 = E2 / R4 = (0,5 V)2 / 5,05 mΩ = 49,5 mW
Un rezistor de 1/8 W este suficient pentru R4, unul de 1/2 W pentru R3 şi unul de 5 W pentru R2. Totuşi, rezistorii îşi menţin acurateţea pentru o perioadă mult mai îndelungată de timp dacă nu funcţionează foarte aproape de valoarea maximă admisă; prin urmare, o supra-dimensionare a rezistorilor R2 şi R3 ar fi binevenită. Dar, rezistorii de precizie cu o putere nominală de 50 W sunt extrem de rari şi de scumpi. Singura modalitate este realizarea la comandă a acestora.
8.4.1 Măsurarea curentului cu un rezistor de şunt şi un voltmetru
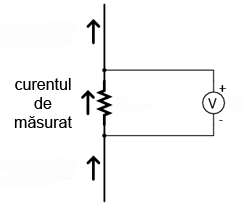
În unele cazuri, rezistorii de şunt sunt utilizaţi în combinaţie cu voltmetre cu rezistenţa de intrare ridicată pentru măsurarea curenţilor. Curentul prin voltmetru va fi suficient de mic pentru a-l putea neglija, iar rezistenţa de şunt poate fi dimensionată în funcţie de numărul de volţi sau milivolţi produşi pentru fiecare amper de curent.
De exemplu, dacă rezistorul de şunt din figura de mai sus ar fi dimensionat la o valoare de exact 1 Ω, pentru fiecare creştere de un amper, căderea de tensiune la bornele acestuia va creşte cu un volt. Indicaţia voltmetrului va putea fi considerată ca fiind direct legată valoarea curentului prin şunt. Pentru valori foarte mici ale curentului, rezistenţa de şunt trebuie să fie mare pentru a putea genera tensiuni mai mari pentru fiecare unitate de curent, extinzând astfel gama valorilor măsurate cu voltmetrul spre mărimi foarte mici. Această metodă de măsurare este des întâlnită în aplicaţiile industriale. Desigur, în acest caz, scala voltmetrului poate fi modificată/înlocuită pentru a putea citi direct valorile curentului.
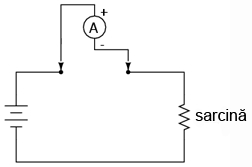
Utilizarea unui rezistor de şunt în combinaţie cu un voltmetru poate simplifca operaţiile de măsurare ale curenţilor, atunci când acestea sunt dese, În mod normal, atunci când măsurăm curentul dintr-un circuit cu ampermetrul, circuitul trebuie întrerupt (deschis), iar ampermetru conectate între cele două capete libere închizând astfel din nou circuitul.
măsurarea curentului cu ajutorul unui voltmetru; util în cazul unui circuit asupra căruia sunt necesare măsurători dese ale valorii
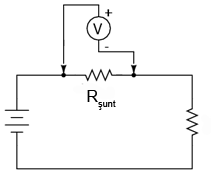
Dacă avem un circuit în care această operaţie trebuie realizată des, sau dacă dorim simplificarea procesului de măsură, putem plasa permanent un rezistor de şunt între cele două capete rămase libere după deschiderea circuitului. Curentul poate fi măsurat de acum încolo cu ajutorul unui voltmetru, fără a necesita întreruperea circuitului la fiecare măsurătoare.
Desigur, dimensiunea şuntului trebuie să fie suficient de mică pentru a nu afecta funcţionarea normală a circuitului în care este introdus. Va exista o mică eroare de măsură datorită prezenţei şuntului, dar aceasta se încadrează în limite acceptabile.

8.5 Impactul ampermetrului asupra circuitului
8.5.1 Ampermetrul ideal
Asemenea voltmetrelor, şi ampermetrele tind să influenţeze cantitatea de curent din circuitele în care sunt conectate. Totuşi, spre deosebire de voltmetrul ideal, rezistenţa interna a ampermetrului ideal este zero. Motivul îl reprezintă o cădere de tensiune cât mai mică la bornele acestuia. Observaţi că acest lucru este exact opus voltmetrului (curent cât mai mic consumat din circuit).
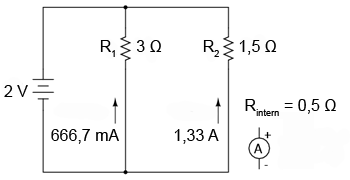
Să vedem un exemplu pentru identificarea efectelor unui ampermetru asupra circuitului. Atunci când ampermetrul nu este introdus în circuit, curentul prin rezistorul de 3 Ω este de 666,7 mA, iar curentul prin rezistorul de 1,5 Ω este de 1,33 A.
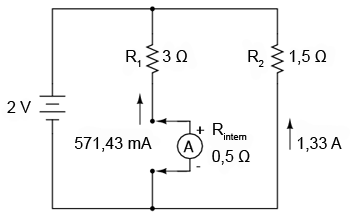
Dacă ampermetrul cu care efectuăm măsurătorile are o rezistenţă internă de 0,5 Ω, introducerea acestuia într-una din ramurile circuitului va afecta puternic circuitul. Modificând practic rezistenţa ramurii din stânga de la 3 Ω la 3,5 Ω, ampermetrul va indica un curent de 571, 43 mA în loc de 666,7 mA.
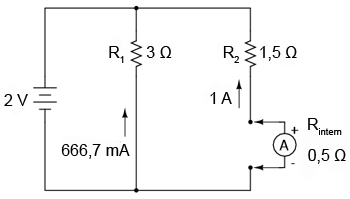
Introducerea ampermetrului în ramura din dreapta va avea un efect şi mai mare asupra curentului din aceasta. În acest caz, curentul de ramură va fi de 1 A, în loc de 1,33 A, din cauza creşterii rezistenţei prin introducerea ampermetrului.
La utilizarea ampermetrelor standard, ce se conectează în serie cu circuitul de măsurat, reproiectarea aparatului pentru o rezistenţa mai mică între cele două terminale, nu este practică sau poate chiar imposibilă. Totuşi, dacă măsurăm curentul cu ajutorul unui voltmetru şi a unui rezistor de şunt, cel mai indicat lucru este să alegem o rezistenţa cât mai mică. Orice rezistenţă adiţională introdusă în circuitul iniţial, va duce la modificarea comportamentului acestuia.
8.5.2 Cleştele ampermetric (clampmetrul)
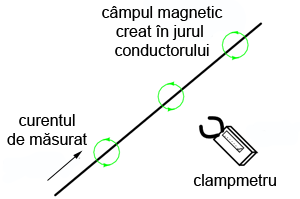
O metodă ingenioasă de reducere a impactului pe care îl are un aparat de măsură asupra circuitului, este utilizarea conductorului ca parte integrantă a ampermetrului. Toţi conductorii produc un câmp magnetic în jurul lor la trecerea curentului prin ei; valoarea acestui câmp magnetic este direct proprţională cu valoarea curentului prin conductor. Construind un instrument pentru măsurarea puterii acelui câmp magnetic, se poate evita contactul direct şi întreruperea circuitului. Un astfel de ampermetru poartă numele de clampmetru sau cleşte ampermetric.
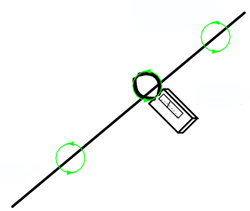
Acesta constă practic din doi cleşti ce se pun în jurul conductorului. Cu ajutorul acestor dispozitive se pot realiza măsurător rapide şi sigure, în special în cazul circuitelor de putere. Datorită faptului că clampmetrul nu introduce nicio rezistenţa suplimentară în circuitul de test, nu va exista practic nicio eroare de măsurătoare în acest caz.
8.6 Ohmmetrul
8.6.1 Scopul ohmmetrului
Chiar daca ohmmetrele mecanice (analogice) sunt folosite destul de rar astăzi, fiind înlocuite de instrumentele digitale, modul lor de funcţionare este foarte interesant şi merită prin urmare studiat.
Scopul unui ohmmmetru este, desigur, măsurarea rezistenţei conectată între bornele sale. Citirea valorii rezistenţei se face prin observarea deplasării unui mecanism de deplasare acţionat de un curent electric. Prin urmare, ohmmetrul trebuie echipat cu o sursă internă de tensiune pentru a crea curentul necesar acţionării deplasării. Avem nevoie, de asemenea, de rezistenţe suplimentare pentru a permite trecerea unui curent necesar şi suficient prin mecanismul de deplasare, pentru oricare valoare a rezistenţei de măsurat.
8.6.2 Realizarea unui ohmmetru simplu
Începem cu un circuit simplu, format din mecanismul de măsură şi o baterie:
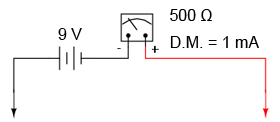
Când avem o rezistenţă infinită (nu există continuitate între cele două sonde), curentul prin circuitul intern al ohmmetrului este zero. În acest caz, nu avem nicio deplasare, iar acul indicator este poziţionat în partea stângă a scalei de valori. Din acest punct de vedere, indicaţia ohmmetrului este chiar „inversă”, deoarece valoarea maximă (infinit) este la stânga scalei. Indicaţia voltmetrelor şi ampermetrelor este chiar inversă.
Dacă sondele acestui ohmmetru sunt conectate împreună (scurt-circuitate, rezistenţa 0 Ω), curentul prin aparatul de măsură va fi maxim. Valoarea acestui curent este limitată doar de tensiunea bateriei şi de rezistenţa internă a mecanismului de măsură:
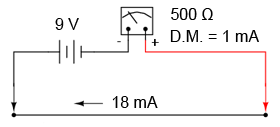
Cu o tensiune a bateriei de 9 V şi o rezistenţa internă a mecanismului de deplasare de doar 500 Ω, curentul prin circuit va fi de 18 mA. Această valoare este mult peste deplasarea maximă (D.M. = 1 mA) permisă de dispozitivul nostru. Un asemenea exces va duce cu siguranţa la distrugerea aparatului.
Pe lânga aceste aspecte, dispozitivul de mai sus nu va fi nici foarte practic. Dacă partea din stânga a scalei reprezintă o rezistenţă infinită, atunci partea din drepta (deplasare maximă) ar trebui să reprezinte 0 Ω. Trebuie să ne asigurăm de faptul că deplasarea acului indicator este maximă spre dreapta doar când sondele sunt conectate împreună (scurt-circuitate). Acest lucru se realizează prin adăugarea unei rezistenţe serie în circuitul aparatului de măsură:
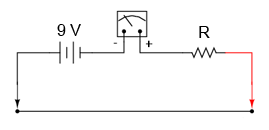
Pentru determinarea valorii lui R, calculăm rezistenţa totală din circuit necesară pentru a limita curentul la 1 mA (curentul necesar pentru deplasarea maximă). Ştim de asemenea că avem o diferenţa de potenţial de 9 V, dinspre baterie. Valoarea rezistenţei pe care o căutăm va fi diferenţa dintre această rezistenţă totală şi rezistenţa internă a aparatului de măsură:
Rtotal = E / I = 9 V / 1 mA Rtotal = 9 kΩ R = Rtotal - 500 Ω = 8,5 kΩ
8.6.3 Împărţirea scalei
Acum că avem valoarea corectă a rezistorului R, mai avem o problemă: scala aparatului de măsură. După cum se ştie deja, în stânga scalei avem infinit, iar în drepta zero. În afara faptului că această scală este inversă faţă de cea a voltmetrelor şi ampermetrelor, mai are o ciudăţenie: valorile între care se face citirea se află între două extreme (infinit şi zero). În cazul celorlalte aparate de măsură, valorile citite se află între zero şi o anumită valoare (10 V, 1 A, etc.). Prin urmare, ce valoare reprezintă mijlocul scalei ?! Ce valoare se află exact între infinit şi zero?
Răspunsul acestui paradox poartă numele de „scală ne-liniară”. Pe scurt, scala unui ohmmetru nu reprezintă o trecere liniară de la zero spre infinit, pe măsură ce acul indicator se deplasează dinspre dreapta spre stânga. Iniţial, indicaţia este maximă spre dreapta (rezistenţa zero), iar valorile rezistenţelor se adună din ce în ce mai rapid una lângă cealaltă pe măsură ce trecem în partea stângă a scalei:
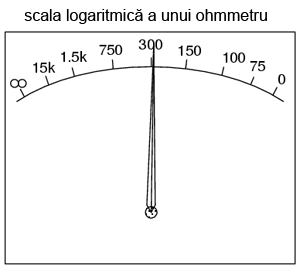
Nu ne putem apropia de infinit printr-o manieră liniară, pentru că scala nu ar ajunge niciodată acolo! Cu o scală ne-liniară, cantitatea de rezistenţa acoperită de o anumită distanţă creşte pe măsură ce scala se apropie de infinit. În acest caz, putem spune că infinitul este o „valoare” ce poate fi atinsă.
Mai există totuşi încă o nelămurire legată de scala noastră. Care este valoarea necesară a rezistenţei dintre sonde, astfel încât acul indicator să se regăsească la jumătatea scalei? Cunoaştem că deplasarea maximă este 1 mA. Atunci, 0,5 mA (500 µA) este valoare curentului necesară pentru această deplasare la mijlocul scalei. Păstrâng bateria de 9 V în circuit, obţinem următorul rezultat:
Rtotal = E / I = 9 V / 500 µA Rtotal = 18 kΩ
Cu o rezistenţa internă de 500 Ω, şi un rezistor serie de 8,5 kΩ, ne mai rămân 9 kΩ pentru o rezistenţa de test externă (conectată între sonde), pentru o deplasare la jumătatea a scalei. Cu alte cuvinte, rezistenţa de test necesară unei deplasări la jumătatea scalei a acului indicator, este egală în valoare cu rezistenţa serie internă totală a aparatului de măsură. Aplicând din nou legea lui Ohm, putem determina valoarea rezistenţei de test pentru o deplasare la 1/4 şi 3/4 a scalei:
Deplasare la 1/4 (0,25 mA):
Rtotal = E / I = 9 V / 250 µA Rtotal = 36 kΩ Rtest = Rtotal
- Rintern Rtest = 36 kΩ - 9 kΩ Rtest = 27 kΩ
Deplasare la 3/4 (0,75 mA):
Rtotal = E / I = 9 V / 750 µA Rtotal = 12 kΩ Rtest = Rtotal
- Rintern Rtest = 12 kΩ - 9 kΩ Rtest = 3 kΩ
Prin urmare, scala finală a ohmmetrului arată astfel:
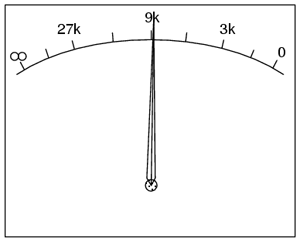
8.6.4 Dezavantajele metodei de mai sus
O problemă majoră a acestui aranjament constă în necesitatea utilizării unei baterii precise. În caz contrar, valorile citite nu vor fi reale. Dacă tensiunea bateriei scade (acest lucru se întâmplă cu toate bateriile chimice), ohmmetrul va pierde din precizie. Cu rezistorul de scală conectat în serie şi la o valoare constantă de 8,5 kΩ, o descreştere a tensiunii bateriei va însemna că deplasarea acului indicator nu se va realiza înspre poziţia dreapta-maximă la conectarea sondelor împreună (0 Ω). Identic, o rezistenţa de test de 9 kΩ nu va reuşi să deplaseze acul indicator la exact jumătatea scalei de măsură, dacă tensiunea bateriei scade.
Desigur, există metode de compensare a acestei pierderi de tensiune a bateriei. Aceste „artificii” însă nu rezolvă în totalitate problema, şi sunt considerate în cel mai bun caz doar aproximaţii. Din acest motiv, şi datorită scalei neliniare, acest tip de ohmmetru nu poate fi în niciun caz considerat un instrument de precizie.
Mai există încă o particularitate a ohmmetrelor ce trebuie menţionată: acestea funcţionează corect doar atunci când măsoară o rezistenţă ce nu este alimentată de o sursă de curent sau de tensiune. Cu alte cuvinte, nu putem măsură rezistenţa cu un ohmmetru, atunci când circuitul este alimentat (conectat la o sursă de tensiune). Motivul este simplu: indicaţia precisă a ohmmetrului se bazează pe faptul că singură sursă de tensiune din circuit este propria sa baterie internă. Prezenţa unei alte căderi de tensiune la bornele componentului supus măsurătorii va da peste cap funcţionarea corectă a ohmmetrului. Dacă această cădere de tensiune este suficient de mare, poate duce chiar la distrugerea acestuia.
8.7 Ohmmetre pentru tensiuni înalte
8.7.1 Limitările ohmmetrelor de joasă tensiune
Majoritatea ohmmetrelor de tipul celui prezentat în secţiunea precedentă folosesc o baterie cu o tensiune relativ mică, de 9 V sau chiar mai puţin. Acest lucru este suficient pentru măsurarea rezistenţelor cu valori mai mici de câţiva mega-ohmi (MΩ). Pentru a măsura însă rezistenţe extrem de mari, o baterie de 9 V nu este suficientă pentru generarea unui curent necesar acţionării mecanismului electromecanic de deplasare.
De asemena, după cum am discutat deja, rezistenţa nu este tot timpul o valoare stabilă (liniară). Acest lucru este valabil în special în cazul materialelor ne-metalice. Un dielectric format dintr-o mică porţiune de aer, prezintă (aproximativ) următorul grafic curent-tensiune:
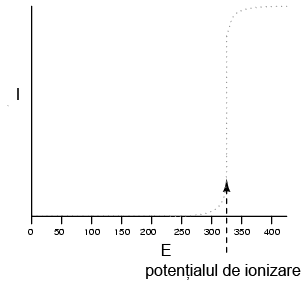
Deşi acesta este un exemplu extrem de conducţie non-liniară, aceleaşi proprietăţi izolatoare/conductoare se regăsesc şi în cazul altor substanţe când sunt supuse tensiunilor înalte. Evident, un ohmmetru echipat cu o baterie de tensiune joasă ca şi sursă de putere, nu poată măsura rezistenţa gazului în zona potenţialului de ionizare, sau la punctul de străpungere a unui dielectric. Dacă este necesară măsurarea unor astfel de rezistenţe, avem nevoie de un ohmmetru echipat cu o sursă de tensiune înaltă.
8.7.2 Modul de proiectare al ohmmetrelor de tensiune înaltă
Metoda cea mai directă de măsurare a rezistenţelor folosind tensiuni înalte, constă în simpla înlocuire a bateriei, păstrând structura precedentă a ohmmetrului neschimbată:
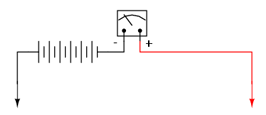
Totuşi, cunoscând faptul că rezistenţa unora dintre materiale tinde să se modifice odată cu variaţia tensiunii aplicate, ar fi avantajos dacă am putea selecta tensiunea de funcţionare a ohmmetrului în funcţie de condiţiile de realizare a măsurătorii:
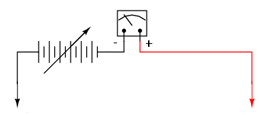
Din păcate, această situaţie crează o problemă de calibrare a ohmmetrului. Dacă deplasarea acului indicator este maximă cu o anumită valoare a curentului prin aparat, scala aparatului de măsură (în ohmi) se va modifica odată cu variaţia tensiunii sursei de alimentare. Imaginaţi-vă că am conecta o rezistenţa stabilă la bornele ohmmetrului, variind tensiunea sursei de alimentare: pe măsură ce tensiunea creşte, curentul prin aparat va fi din ce în ce mai mare; deplasarea acului indicator va fi la rândul ei din ce în ce mai mare.
8.7.3 Megohmmetrul
Avem nevoie prin urmare de un sistem electromecanic ce produce o deplasare stabilă, indiferent de rezistenţa de măsurat şi de tensiunea aplicată. Această nevoie poate fi îndeplinită folosind un sistem electromecanic special, sistem tipic megohmmetrelor:
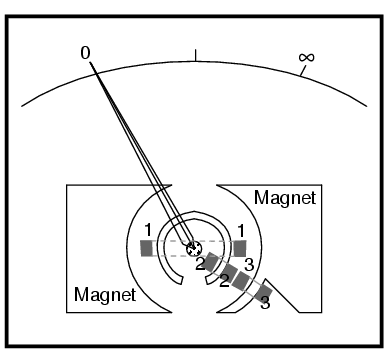
Blocurile rectangulare numerotate din figura de mai sus reprezintă secţiuni transversale al bobinelor. Toate cele trei bobine se deplasează odată cu acul indicator. Nu există niciun arc care să readucă acul la poziţia iniţială. Când aparatul nu este alimentat, acul indicator va „pluti” într-o poziţie aleatoare. Electric, bobinele sunt conectate astfel:
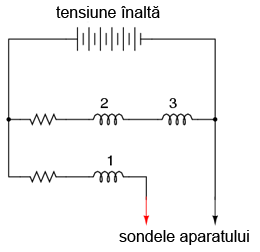
Când avem o rezistenţă infinită între cele două sonde (circuit deschis, precum în figura de sus), singurul curent existent în circuit va fi prin bobinele 2 şi 3, dar nu şi prin bobina 1. Când sunt alimentate, aceste bobine încearcă să se alinieze în spaţiul liber dintre cei doi poli magnetici. Acul indicator se va deplasa spre dreapta scalei (infinit):
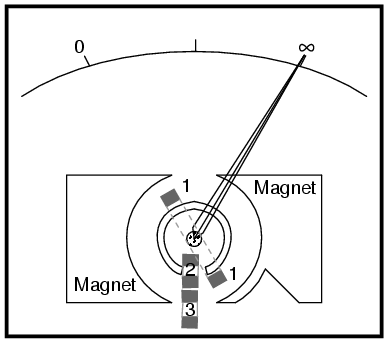
Existenţa unui curent prin bobina 1 (printr-o rezistenţa de măsurat conectată între cele două sonde de măsură) tinde să ducă acul indicat spre stânga scalei (zero). Valorile rezistenţelor interne ale sistemului de măsură sunt calibrate astfel încât, în cazul în care sondele sunt scurt-circuitate, acul indicator indică exact 0 Ω.
Datorită faptului că orice variaţie a tensiunii bateriei interne va afecta cuplul generat de ambele seturi de bobine (bobinele 2 şi 3, ce deplasează acul indicator spre dreapta, şi bobina 1 şi deplasează acul spre stânga), aceste variaţii nu vor avea niciun efect asupra setării deplasării. Cu alte cuvinte, precizia sistemului de măsură a acestui ohmmetru nu este afectată de tensiunea bateriei: o anumită valoare a rezistenţei de măsurat va produce o anumită deplasare a acului indicator, indiferent de valoarea tensiunii produsă de baterie.
8.8 Multimetre
Am văzut modul în care un sistem electromecanic poate funcţiona pe post de voltmetru, ampermetru sau ohmmetru prin simpla conectare a unor reţele externe de rezistori. Ne putem gândi că am putea realiza un aparat de măsură universal (multimetru), în care să fie încorporate toate funcţiile de mai sus. Acest lucru se realizează practic prin utilizarea corespunzătoare a contactelor şi rezistorilor.
8.8.1 Voltmetru/ampermetru analogic
Schema de principiu a unui voltmetru/ampermetru analogic simplu, arată astfel:
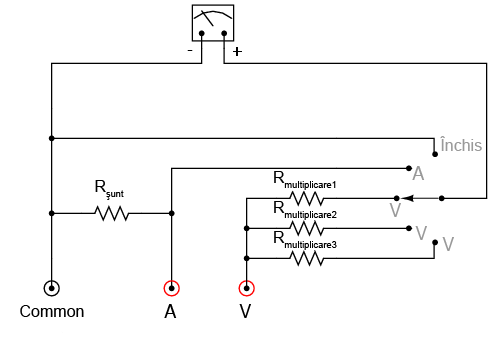
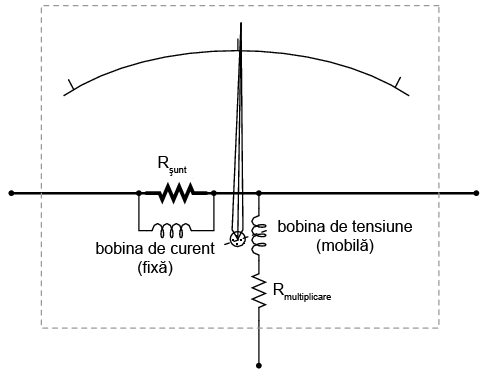
În cele trei poziţii de jos ale comutatorului, mecanismul de detecţie al aparatului este conectat la prizele „common” şi V printr-unul din cei trei rezistori serie (Rmultiplicare). În acest caz, aparatul se comportă precum un voltmetru. În cea de a patra poziţie, mecanismul de deplasare este conectat în paralel cu rezistorul de şunt (Rşunt. Astfel, aparatul este în acest caz un ampermetru. Curentul intră pe la priza „common” şi iese pe la priza A. În ultima poziţie, mecanismul de deplasare este deconectat de la ambele prize roşii (V şi A), dar scurcircuitat prin intermediul comutatorului.
8.8.2 Adăugarea unui ohmmetru
Dacă dorim şi adăugarea unui ohmmetru aparatului de măsură de mai sus, putem înlocui una din cele trei poziţii ale voltmetrului, astfel:
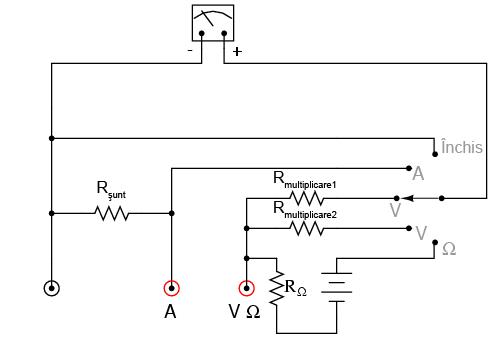
Cu toate cele trei funcţii disponibile, acest multimetru mai este cunoscut şi sub numele de volt-ohm-miliampermetru.
8.9 Terminali tip Kelvin şi rezistori de precizie
8.9.1 Măsurarea rezistenţelor aflate la distanţă
Să presupunem că vrem să măsurăm rezistenţa unui anumit component ce se află la o distanţă destul de mare de aparatul nostru de măsură (ohmmetru). Un asemenea scenariu va crea probleme, deoarece ohmmetrul măsoară rezistenţa totală din bucla de circuit. Aici este inclusă şi rezistenţa conductorilor (Rfir) ce realizează conexiunea ohmmetrului cu rezistenţa de măsurat (Rmăsură):
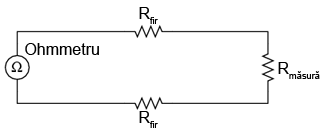
În mod normal, rezistenţa fireloc conductoare este foarte mică. Dar, dacă firele conductoare sunt foarte lungi, sau în cazul în care componentul de măsurat are o rezistenţă foarte mică, eroarea de măsură introdusă de conductori poate fi substanţială:
indicaţia ohmmetrului = Rfir + Rmăsură + Rfir
8.9.2 Măsurarea rezistenţei cu o combinaţie ampermetru-voltmetru
O metodă ingenioasă de măsurare a unei rezistenţe în acest caz, presupune utilizarea împreună a unui ampermetru şi a unui voltmetru. Ştim din legea lui Ohm că rezistenţa este egală cu raportul dintre tensiune şi curent (R = E / I). Putem determina prin urmare rezistenţa componentului dacă măsurăm curentul ce trece prin el şi căderea de tensiune la bornele sale:
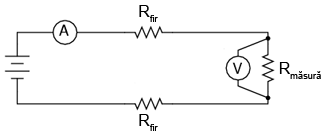
Valoarea curentului este aceiaşi în întreg circuitul, deoarece este un circuit serie. Întrucât măsurăm doar căderea de tensiune la bornele rezistenţei de măsurat (şi nu pe rezistenţele conductorilor), rezistenţa calculată cu ajutorul legii lui Ohm reprezintă doar rezistenţa componentului în cauză:
Rmăsură = indicaţia voltmetrului / indicaţia ampermetrului
Dar, voltmetrul se află în apropierea componentului de măsurat, ceea ce este imposibil în situaţia de faţă (am convenit că dorim să măsură rezistenţa componentelor aflate la o distanţa apreciabilă faţă de aparatele noastre de măsură). Prin urmare, dacă ar fi să conectăm voltmetrul la o distanţa apreciabilă faţă de component, vom introduce din nou rezistenţa „parazită” a firelor conductoare în circuit. Ce este de făcut în acest caz?
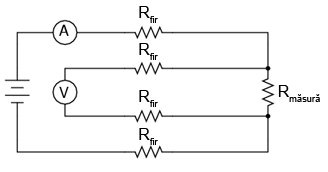
Dacă suntem puţin mai atenţi, putem observa că nu există nicio problemă legată de căderea de tensiune în lungul conductorilor, deoarece valoarea curentului prin conductorii voltmetrului este minusculă. Prin urmare, căderea de tensiune în lungul conductorilor este neglijabilă. Indicaţia voltmetrului este aproape identică în cele două cazuri: voltmetru conectat în apropierea componentului de măsurat şi voltmetru conectat la o distanţă apreciabilă:
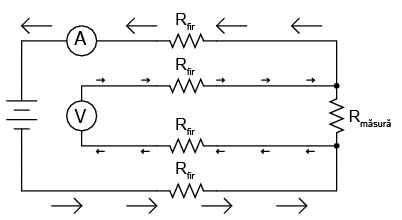
Orice cădere de tensiune existentă pe conductorii principali nu va fi măsurată de voltmetru. Precizia măsurătorii poate fi îmbunătăţită dacă reducem curentul prin volmetru la o valoare minimă, fie folosind un aparat de măsură de calitate (curent mic pentru deplasare maximă), fie un sistem cu detector de nul.
8.9.3 Metoda Kelvin (metoda celor patru conductori)
Această metodă de măsurare ce evita erorile cauzate de rezistenţa conductorilor poartă numele de metoda Kelvin, sau metoda celor patru conductori. Există anumiţi terminali speciali, denumiţi terminali Kelvin, ce sunt special realizaţi pentru a facilita acest tip de măsurători:
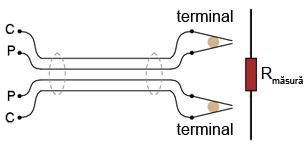
Terminalii/clemele tip crocodil (banane) au ambele jumătăţi ale braţului comune din punct de vedere electric (de obicei în zona articulaţiei). În cazul terminalilor Kelvin însă, cele două jumătăţi sunt izolate între ele în zona articulaţie. Singurul contact se realizează în zona vârfurilor ce se „prind” pe conductorul sau pe terminalul componentului de măsurat. Astfel, curentul prin braţele „C” (curent) nu trece prin braţele „P” (potenţial, sau tensiune) şi nu va exista o cădere de tensiune în lungul lor care să ducă la erori de măsură:
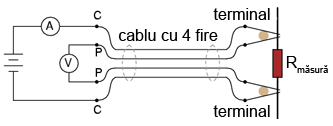
8.9.4 Rezistori de şunt de precizie înaltă
Acelaşi principiu de utilizare a diferitelor puncte de conctat pentru măsurarea curentului şi a tensiunii poate fi folosit în cazul rezistorilor de şunt de precizie pentru măsurarea valorilor mari de curent. După cum am mai discutat, rezistorii de şunt sunt folosiţi pe post de dispozitive de măsură de curent. Căderea de tensiune la bornele acestora depinde strict de valoare curentului ce-i străbate, această cădere de tensiune fiind măsurată cu un voltmetru. În acest caz, un şunt de precizie „transformă” valoarea curentului în tensiune. Curentul poate fi măsurat cu o precizie ridicată prin măsurarea căderii de tensiune la bornele şuntului:

Măsurarea curentului cu ajutorului unui rezistor de şunt şi un voltmetru este indicată în aplicaţiile de curent înalt. În astfel de cazuri, rezistenţa şuntului are valori de ordinul miliohmilor sau microohmilor. Căderea de tensiune la bornele sale va fi foarte mică, chiar şi pentru o valoare maximă a curentului de măsurat. O rezistenţă aşa de mică este comparabilă cu rezistenţa firelor conductoare. Acest lucru înseamnă că tensiunea măsurată la bornele unui astfel de şunt trebuie măsurată astfel încât să se evite introducerea unei erori de măsură datorate căderilor de tensiune din lungul conductorilor dintre voltmetru şi şunt. Pentru ca voltmetrul să măsoare doar căderea de tensiune la bornele şuntului, fără nicio altă cădere de tensiune parazită datorată fireloc conductoare, şunturile sunt adesea prevăzute cu patru terminali:
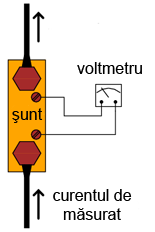
8.9.5 Rezistori de precizie cu patru terminali
În aplicatii metrologice (metrologie = "ştiinţă măsurătorilor”), unde acurateţea este de o importanţă crucială, rezistorii „standard” de precizie sunt prevăzuţi de asemenea cu patru terminali: doi pentru transportul curentului de măsurat, şi doi pentru măsurarea căderii de tensiune cu ajutorului voltmetrului. În acest mod, voltmetru măsoară doar căderea de tensiune pe rezistorul de precizie, fără introducerea altor tensiuni parazite datorită firelor conducătoare sau a rezistenţelor datorate contactelor dintre fire şi terminale.
Observaţi că rezistorul de precizie standard de 1 Ω din figura de mai jos are patru terminali: cei doi terminali mari pentru curent şi cei doi terminali mai mici pentru tensiune:

Trebuie să facem observaţia că rezistenţa măsurată astfel, folosind atât un voltmetru cât şi un ampermetru, este supusă unei erori compuse. Datorită faptului că rezultatul final depinde de precizia de măsură a ambelor instrumente, precizia măsurătorii finale s-ar putea să fie mai mică decât cea a fiecărui instrument individual. De exemplu, dacă precizia ampermetrului este de +/- 1%, iar cea a voltmetrului este şi ea de +/- 1%, orice măsurătoare ce depinde de indicaţia ambelor instrumente are o precizie de +/- 2% (valoarea reală este mai mică sau mai mare cu 2% decât valoarea măsurată).
O precizie sporită poate fi obţinută prin înlocuirea ampermetrului cu un rezistor de precizie standard, folosit pe post de şunt de măsurare a curentului. Şi în acest caz va exista o eroare compusă din eroarea rezistorului cu cea a voltmetrului utilizat pentru măsurarea căderii de tensiune. Această eroare va fi însă mai mică decât eroare prezentă în cazul utilizării unui aranjament voltmetru + ampermetru, datorită faptului că precizia unui rezistor standard este mult mai mare decât precizia unui ampermetru obişnuit. Folosind terminali de tip Kelvin pentru realizarea contactelor cu rezistenţa de măsură, circuitul arată astfel:
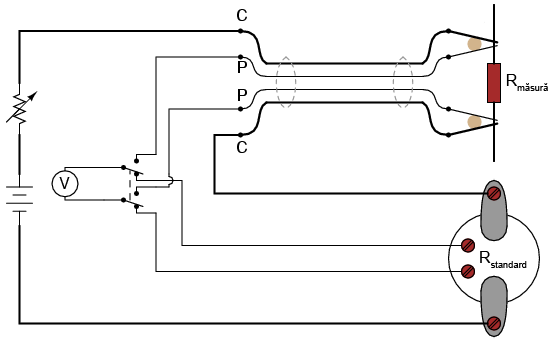
Toţi conductorii din figura de mai sus prin care trece curent sunt reprezentaţi cu linie îngroşată, pentru a face distincţie între conductorii.
8.10 Circuite în punte - puntea Wheatstone şi Thomson
Circuitele în punte se foloesc de un detector de nul pentru a compara două tensiuni. Principiul este asemănător unei balanţe de laborator ce compară două greutăţi pentru a indica egalitatea lor. Spre deosebire de circuitul „potenţiometric” utilizat pentru a măsura pur şi simplu o cădere de tensiune necunoscută, circuitele în punte pot fi folosite pentru a măsura o varietate de mărimi electrice, una din ele fiind rezistenţa.
8.10.1 Puntea Wheatstone
Circuitul în puncte standard, numit adeasea şi punte Wheatstone, arată astfel:
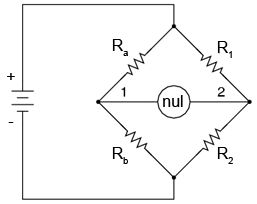
Atunci când căderea de tensiune între punctul 1 şi borna negativă a bateriei este egală cu tensiunea dintre punctul 2 şi borna negativă a bateriei, detectorul de nul va indica valoarea zero. În acest caz spunem că puntea este „echilibrată”. Starea de echilibru a balanţei este dependentă da raporturile Ra / Rb şi R1 / R2 şi este independentă de tensiunea de alimentare (a bateriei).
Pentru măsurarea rezistenţelor folosind puntea Wheatstone, rezistenţa necunoscută se conectează în locul rezistorului Ra sau Rb. Celelalte trei componente sunt dispozitive de precizie, a căror rezistenţă este cunoscută. Oricare din cei trei rezistori poate fi înlocuit sau ajustat, astfel încât puntea să fie echilibrată. Când se ajunge la echilibru, valoarea rezistorului necunoscut se determină din raporturile rezistenţelor cunoscute.
O cerinţă a acestui sistem de măsură constă în existenţa unor seturi de rezistori variabili de precizie. Din moment ce rezistenţa acestora este cunoscută, pot fi folosiţi ca şi referinţă. De exemplu, dacă folosim o punte Wheatstone pentru a măsura o rezistenţă necunoscută Rx, va trebui să cunoaştem valorile exacte ale celorlalţi trei rezistori în starea de echilibru, dacă dorim să determinăm valoarea lui Rx:
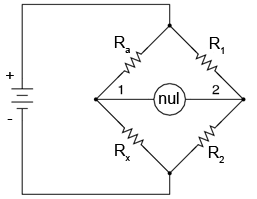
Ecuaţia de echilibru a punţii Wheatstone este următoarea:
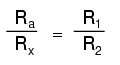
Fiecare din cei patru rezistori a unei punţi poartă numele de braţ. Rezistorul conectat în serie cu rezistenţa necunoscută Rx (Ra în figura de mai sus) poartă de obicei numele de reostat de reglaj. Din fericire, rezistenţele standard precise şi stabile nu sunt aşa de greu de realizat.
Punţile Wheatstone sunt considerate superioare circuitelor de măsură standard prezentate în secţiunea precedentă din punct de vedere al măsurării rezistenţelor. Spre deosebire de acele circuite, punţile Wheatstone sunt liniare şi extrem de precise.
Având la dispoziţie rezistenţe standard de o precizie ridicată şi un detector de nul cu o sensibilitate suficientă, putem măsura rezistenţe cu o precizie de cel puţin +/- 0,05 %. Această metodă este preferată şi indicată pentru măsurarea rezistenţelor de laborator datorită preciziei ridicate.
Există multe variaţii a circuitului în punte Wheatstone de bază. Majoritatea circuitelor în punte de curent continuu sunt folosite pentru măsurarea rezistenţei. Dar circuitele alimentate în curent alternativ pot fi folosite pentru a măsura diferite mărimi electrice precum inductanţă, capapacitate şi frecvenţă.
8.10.2 Puntea Thomson (puntea Kelvin dublă)
O variantă interesantă a punţii Wheatstone o reprezintă puntea dublă Kelvin, cunoscută şi sub numele de punte Thomson. Aceast circuit este utilizat pentru măsurarea rezistenţelor extrem de mici (sub 1/10 ohmi):
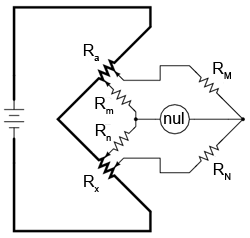
Rezistorii de valoare mică sunt reprezentaţi prin simboluri cu linie îngroşată, la fel şi conductorii (prin care trece un curent mare) la care sunt conectaţi. Această punte „ciudată” poate fi cel mai bine înţeleasă dacă reluăm puntea Wheatstone standard pentru măsurarea rezistenţelor mici, pentru a ajunge apoi, pas cu pas (datorită problemelor întâmpinate), la forma finală a punţii Thomson.
Dacă am dori să folosim o punte Wheatstone standard pentru a măsura rezistenţe de o valoare foarte mica, circuitul ar artăta astfel:
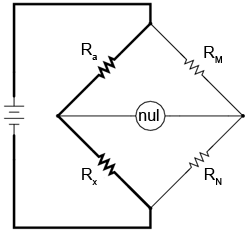
Când detectorul de nul indică o tensiune zero, ştim că puntea este echilibrată iar raporturile Ra / Rb şi RM / RN sunt egale. Cunoscând valorile rezistorilor Ra, RM şi RN putem determina Rx…aproximativ.
Avem totuşi o problemă: contactele şi firele conductoare dintre Ra şi Rx prezintă şi ele o anumită rezistenţă. Aceste rezistenţe parazite pot fi substanţiale în comparaţie cu rezistenţele mici Ra şi Rx. De asemenea, căderea de tensiune pe aceste rezistenţe parazite va fi suficient de mare, ducând la un curent mare prin ele. Toate aceste lucruri vor afecta indicaţia detectorului de nul, şi prin urmare, starea de echilibru a punţii:
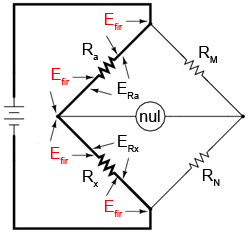
Din moment ce nu dorim măsurarea acestor rezistenţe parazite, ci doar a rezistenţei Rx, trebuie găsita o modalitate de corectare a detectorului de nul astfel încât acesta să nu fie influenţat de căderile de tensiune din lungul acestor rezistenţe parazite. În cazul în care conectăm detectorul de nul şi braţele RM / RN direct la bornele rezistorilor Ra şi Rx, ne vom apropia de o soluţia mai practică:
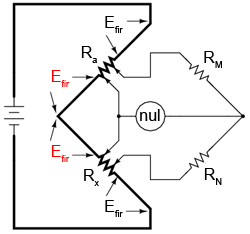
În această configuratie, cele două căderi de tensiune Efir din partea de sus şi de jos nu au niciun efect asupra detectorului de nul şi nu vor influenţa precizia măsurătorii lui Rx. Totuşi, celelalte două căderi de tensiune Efir vor cauza probleme.
Cunoscând faptul că partea stângă a detectorului de nul trebuie conectată la cele două borne ale rezistorilor Ra şi Rx pentru evitarea introducerii căderilor de tensiune Efir în bucla detectorului de nul, şi că orice conductor ce face legătura cu cele două terminale va conduce el însuşi un curent substanţial (ce va duce la căderi de tensiune parazite adiţionale), singura soluţie în această situaţie este realizarea unui drum puternic rezistiv între partea de jos a rezistorului Ra şi partea de sus a rezistorului Rx:
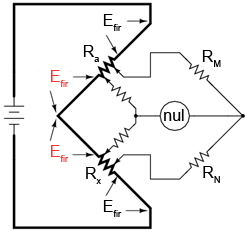
Putem controla căderile de tensiune parazite între Ra şi Rx prin dimensionarea celor doi rezistori noi, astfel încât raportul celui de sus cu cel de jos să fie egal cu raportul celor două braţe de pe partea celalată a detectorului de nul. Acesta este şi motivul pentru care aceşti rezistori au fost denumiţi Rm şi Rn în schema iniţială a puncţii Thomson: pentru a scoate în evidenţa proporţionalitatea lor cu rezistorii RM şi RN:

Raportul Rm / Rn fiind egal cu raportul RM / RN, braţul Ra (reostatul) este ajustat până în momentul în care detectorul de nul indică echilibrul punţii. În acest moment putem spune că Ra / Rx este egal cu RM / RN. Putem calcula Rx cu următoarea ecuaţie:
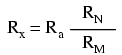
De fapt, ecuaţia de echilibru a punţii Thomson este următoarea:
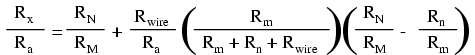
unde Rfir este rezistenţa firului conductor gros dintre rezistenţa standard de jos Ra şi rezistenţa de test Rx.
Atâta timp cât raportul dintre RM şi RN este egal cu raportul dintre Rm şi Rn, ecuaţia de echilibru nu este mai complexă decât cea a punţii Wheatstone normale. Rx / Ra va fi egal cu RN / RM, deoarece ultimul termen al ecuaţiei va fi zero, anulând efectele tuturor rezistorilor cu excepţia lui Rx, Ra, RM şi RN.
8.10.3 Observaţii asupra punţii Thomson
În multe cazuri, RM=Rm şi RN = Rn. Totuşi, cu cât rezistenţele Rm şi Rn sunt mai mici, cu atât detectorul de nul va fi mai sensibil, deoarece rezistenţa conectată în serie cu el va fi mai mică. Creşterea sensibilităţii detectorului este un lucru bun, deoarece permite detectarea unor dezechilibre mult mai mici, şi prin urmare, atingerea unei situaţii de echilibru mult mai precise. Din această cauză, unele punţi Thomson folosesc rezistori Rm şi Rn a căror valori sunt spre 1/100 din raportul braţelor opuse (RM şi RN).
Din păcate totuşi, cu cât valorile rezistorilor Rm şi Rn, cu atât vor conduce un curent mai mare, ceea ce va duce la creşterea efectului oricăror rezistenţe prezente la joncţiunea dintre acestea şi rezistorii Ra şi Rx. După cum se poate vedea, instrumentele de precizie înalta necesită luarea în considerare a tuturor factorilor susceptibili de a produce erori de măsură. De cele mai multe ori, cea mai bună soluţie reprezintă un compromis între două sau mai multe tipuri diferite de erori.
8.11 Wattmetrul
Puterea într-un circuit electric este produsul dintre tensiune şi curent. Prin urmare, orice aparat de măsura a puterii trebuie să poată măsură ambele variabile.
Un mecanism de deplasare priectat special pentru măsurarea puterii este mecanismul de tip dinamometru. Structura acestuia este similară modelelor D'Arsonval şi Weston, cu diferenţa că se utilizează o bobină (staţionară) în locul unui magnet permanent pentru generarea câmpului magnetic. Bobina mobilă este în general alimentată de la tensiunea circuitului, iar bobina staţionară este alimentată de curentul circuitului. Într-un cirucuit, o astfel de strucutră arată astfel:
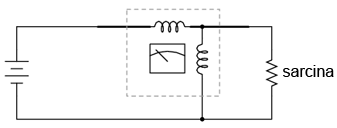
Bobina de sus (orizontală) măsoară curentul, în timp ce bobina de jos (verticală) măsoară căderea de tensiune. La fel ca în cazul voltmetrelor, deplasarea dinamometrului este de obicei conectată în serie cu un rezistor pentru a nu aplica întreaga cădere de tensiune pe mecanism. Asemanător, bobina (staţionară) de curent va fi prevăzută cu rezistori de şunt pentru a diviza curentul în jurul acesteia. Totuşi, de multe ori nu este nevoie de rezistori de şunt, deoarece grosimea conductorului din care este realizată bobina staţionară poate fi oricât de mare (pentru reducerea curentului), fără a influenţa răspunsul aparatului de măsură. Bobina mobilă nu se poate bucura de această „libertate”, deoarece ea trebuie realizată din conductori cât mai usori pentru a o inerţie minimă.
8.12 Realizarea practică a rezistenţelor de calibrare
De multe ori, în cazul realizării circuitelor de măsură, avem nevoie de rezistenţe precise pentru a obţine circuitul dorit. În majoritatea cazurilor însă, valorile necesare ale rezistorilor nu se găsesc pe piaţă. În acest caz, ne vedem nevoiţi să ne construit proprii noştrii rezistori.
8.12.1 Realizarea unei înfăşurări bifilare
O soluţie a acestei dileme este realizarea rezistorilor dintr-un conductor special cu rezistenţă mare. Putem folosi o mică „bobină” ca şi suport pentru înfăşurarea rezultată. Înfăşurarea este astfel realizată încât să elimine orice efecte electromagnetice: lungimea dorită a firului conductor este împăturită în două, şi înfăsurată apoi în jurul bobinei. Astfel, curentul se deplasează în sensul acelor de ceasornic pentru o jumătate din lungimea conductorului şi în sens invers acelor de ceasornic pentru cealaltă jumătate. O astfel de înfăşurare poartă numele de înfăşurare bifilară. Orice câmp magnetic generat de trecerea curentului prin conductor este anulat. De asemenea, un câmp magnetic extern nu poate induce o cădere de tensiune în lungul conductorului:
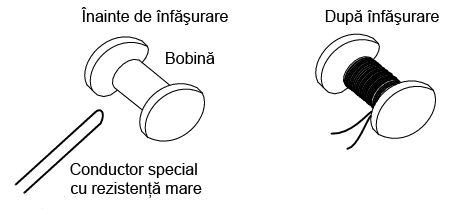
După cum vă puteţi imagina, această se poate dovedi extrem de laborioasă, îndeosebi în cazul în care avem nevoie de mai mulţi rezistori.
8.12.2 Conectarea rezistorilor în combinaţii serie-paralel
O soluţie mai uşoară a acestei probleme constă în conectarea mai multor rezistori cu rezistenţe cunoscute într-o combinaţie serie-paralel pentru a obţine valoarea dorită a rezistenţei. Această soluţie, deşi necesită un timp îndelungat pentru găsirea combinaţiei perfecte, poate fi duplicată mult mai uşor pentru crearea unor rezistenţe multiple cu aceiaşi valoare:
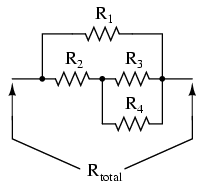
Dezavantajul ambelor metode constă în faptul că ambele rezistenţe rezultate au o valoare fixă. Într-o lume perfectă, mecanismele de deplasare ale aparatelor de măsură nu-şi pierd niciodată puterea magnetică a magneţilor permanenţi din componenţă, temperatura şi timpul nu au niciun efect asupra rezistenţelor componentelor, iar firelor conductoare şi contactele pastrează pentru totdeauna o rezistenţă zero. În această „lume perfectă”, rezistorii cu valori fixe sunt suficienţi. Dar, în realitate, abilitatea de ajustare sau calibrare a instrumentelor în viitor este avantajoasă.
8.12.3 Utilizarea potenţiometrelor
Ne-am putea gândi ca în acest caz să folosim potenţiometre (conectate ca şi reostate, de obicei) ca şi rezistenţe variabile. Potenţiometrul ar putea fi montat în interiorul aparatului de măsură, astfel încât doar o persoană autorizată să-i poată modifica valoarea.
Totuşi, rezistenţa majorităţii potenţiometrelor variază prea mult pentru o deplasarea mică a manetei şi nu pot fi ajustate cu foarte mare precizie. Să presupunem că am dori o rezistenţă de 8,335 kΩ +/- 1 Ω, şi folosim un potenţiometru de 10 kΩ pentru obţinerea ei. O precizie de 1 Ω în cazul unui potenţiometru de 10 kΩ reprezintă 1 parte din 10.000, sau 0,01% din deplasarea maximă a potenţiometrului. Un astfel de rezultat este aproape imposibil de atins folosind un potenţiometru standard. Prin urmare, cum putem obţine valoarea rezistenţei dorite dar cu posibilitatea ajustării ei în viitor?
Soluţia problemei constă în utilizarea unui potenţiometru ca parte a unei combinaţii mai mari de rezistori. Acest lucru va crea un domeniu limitat de selecţie. Să urmărim următorul exemplu:
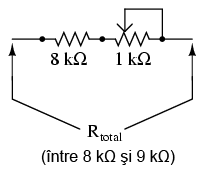
În acest caz, potenţiometrul de 1 kΩ, conectat ca şi reostat, introduce în circuit o rezistenţă variabilă între 0 Ω şi 1 kΩ. Conectat în serie cu rezistorul de 8 kΩ, rezistenţa totală din circuit poate fi ajustată între 8 kΩ şi 9 kΩ. O precizie de +/- 1 Ω reprezintă 1 parte din 1.000, sau 0,1 % din deplasarea maximă a potenţiometrului. Precizia ajustării este de 10 ori mai bună decât în cazul precedent unde am folosit un potenţiometru de 10 kΩ.
Dacă dorim să mărim şi mai mult precizia ajustării - pentru a realiza o rezistenţă de 8,335 kΩ cu o precizie şi mai bună - putem reduce impactul potenţiometrului asupra valorii totale a rezistenţei circuitului prin conectarea unui rezistor de valoare fixă în paralel:
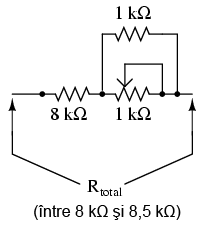
Acum, ajustarea rezistorului se poate face doar în limita a 500 Ω, de la 8 kΩ la 8,5 kΩ. O precizie de +/- 1 Ω este egală cu 1 parte din 500, sau 0,2 %. Sensibilitatea ajustării este în acest caz de două ori mai bună decât înainte. Ajustarea nu va fi totuşi liniară, poziţionarea deplasării potenţiometrului la mijloc nu va rezulta într-o rezistenţă totală de 8,25 kΩ, ci de 8,333 kΩ.
Totuşi, aceasta este o îmbunătăţire a sensibilităţii circuitului, şi reprezintă o soluţie practică pentru problema construirii unei rezistenţe ajustabile pentru un instrument de precizie.