< Curent continuu
5 Circuite electrice serie si paralel
5.1 Ce sunt circuitele „serie” şi „paralel”
Circuitele formate dintr-o singură baterie şi o singură rezistenţă sunt foarte uşor de analizat, dar nu sunt foarte des întâlnite în practică. De obicei circuitele conţin mai mult de două componente conectate între ele
Există două modalităţi de bază în care putem conecta mai mult de două componente într-un circuit: serie şi paralel. Mai jos e un exemplu de circuit serie:
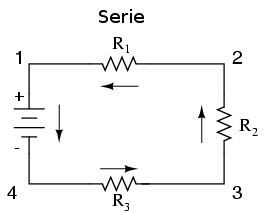
În acest circuit avem 3 rezistori (R1,R2 şi R3) conectaţi într-un singur lanţ de la un terminal al bateriei la celălalt. Caracteristica principală a unui circuit serie este existenţa unei singure căi pentru curgerea electronilor.
Să ne uităm acum şi la celălalt tip de circuit, cel paralel:
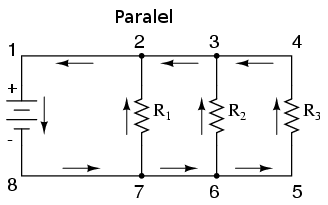
Şi în acest caz avem tot 3 rezistori, dar de data această există mai multe căi pentru curgerea electronilor. Există o cale de la 8 la 7, 2, 1 şi înapoi la 8. Mai exista una de la 8 la 7, 6, 3, 2, 1 şi înapoi la 8. Şi mai există o a treia cale de la 8 la 7, 6, 5, 4, 3, 2, 1 şi înapoi la
- Fiecare cale individuală (prin R1,R2 şi R3) poartă denumirea
de ramură
Caracteristica definitorie pentru un circuit paralel este faptul că toate componentele sunt conectate electric între aceleaşi seturi de puncte. În circuitul de mai sus, punctele 1, 2, 3 şi 4 sunt toate comune din punct de vedere electric. La fel şi punctele 8, 7, 6 şi 5. Toate rezistoarele, precum şi bateria, sunt conectate între aceste două puncte.
Desigur, complexitatea nu se opreşte nici la circuite serie sau paralel! Putem avea de asemenea circuite ce sunt o combinaţie dintre acestea două:
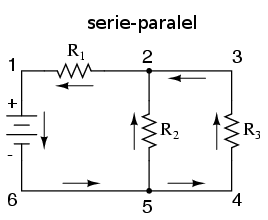
În acest circuit, avem două ramuri prin care electroni pot să circule: una de la 6 la 5, 2, 1 şi înapoi la 6, iar altă ramură de la 6 la 5, 4, 3, 2, 1 şi înapoi la 6. Observaţi cum ambele drumuri trec prin R1 (de la punctul 2 spre punctul 1). În această configuraţie, spunem că R1 şi R2 sunt paralele între ele, în timp ce R1 este în serie cu combinaţia paralelă R1 şi R2.
Idea de bază într-o conexiune serie este conectarea componentelor de la un capăt la altul într-o linie dreaptă:
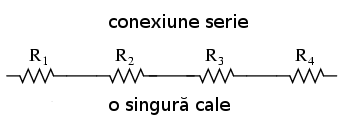
Idea de bază într-o conexiune paralel, pe de altă parte, este că toate componentele sunt conectate între la aceleaşi capete. Într-un circuit pur paralel, nu există niciodată mai mult de două puncte comune, indiferent de numărul componentelor din circuit conectate. Există mai mult de o singură cale pentru deplasarea electronilor, dar o singură cădere de tensiune asupra tuturor componentelor"
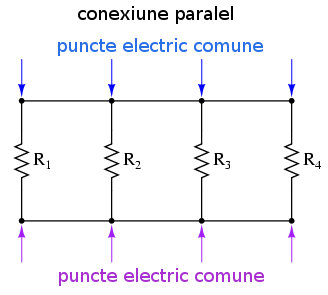
Cele două tipuri de configuraţii, serie şi paralel, prezintă proprietăţi electrice total diferite.
5.2 Circuite serie simple
Să începem cu un circuit electric format dintr-o baterie şi trei rezistori:
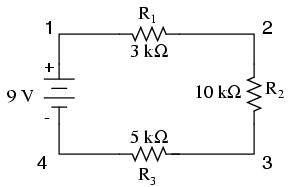
Primul principiu pe care trebuie să-l înţelegem legat de circuitele serie este păstrarea constantă a valorii curentului în întreg circuitul, şi prin urmare, prin fiecare component (prin fiecare component va trece aceeiaşi cantitate de curent electric). Acest lucru se datorează existenţei unei singurei căi pentru trecerea electronilor, iar dacă privim circuitul ca un tub cu bile, putem înţelege de ce rata de deplasare a bilelor trebuie să fie aceeiaşi în orice punct al tubului (circuitului).
După modul în care este aşezată bateria de 9 volţi în circuit, ne putem da seama că deplasarea electronilor se va realiza în sens invers acelor de ceasornic (atenţie, folosim sensul real de deplasare al electronilor în circuit), de la punctul 4 la 3, 2, 1 şi înapoi la 4. Totuşi, avem o singură sursa de tensiune şi trei rezistori. Cum putem aplica legea lui Ohm în acest caz?
Un principiu important de ţinut minte legat de legea lui Ohm, este relaţia dintre tensiune, curent şi a rezistenţă între aceleaşi două puncte din circuit. De exemplu, în cazul unei singure bateri şi a unui singur rezistor în circuit, putem calcula foarte uşor valorile circuitului, pentru că acestea se referă la aceleaşi două puncte din circuit:
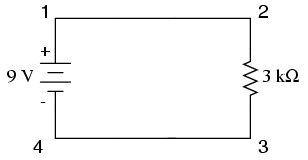
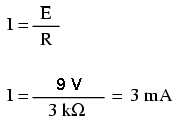
Din moment ce punctele 1 şi 2 sunt conectate împreună printr-un fir de o rezistenţă neglijabilă (la fel şi punctele 3 şi 4), putem spune că punctele 1 şi 2 sunt comune, precum şi că punctele 3 şi 4 sunt comune între ele. De asemenea, ştim faptul că avem o tensiune electromotoare de 9 volţi între punctele 1 şi 4 (direct asupra bateriei), şi pentru că punctele 1 şi 2 cu punctele 3 şi 4 sunt comune, trebuie de asemenea să avem tot 9 volţi între punctele 2 şi 3 (direct asupra rezistorului). Prin urmare, putem aplica legea lui Ohm (I=E/R) asupra curentului prin rezistor, pentru că ştim tensiunea (E) la bornele rezistorului precum şi rezistenţa acestuia. Toţi termenii (E, I, R) se aplică în cazul aceloraşi două puncte din circuit, asupra aceluiaşi rezistor, prin urmare putem folosi legea lui Ohm fără nicio problemă.
Totuşi, în circuitele ce conţin mai mult de un singur rezistor, trebuie să fim atenţi cum aplicăm legea lui Ohm. În exemplul de jos cu trei rezistori în circuit, ştim că avem 9 volţi între punctele 1 şi 4, valoare reprezentând forţa electromotoare disponibilă pentru impingerea electronilor prin conexiunea serie realizată din rezistorii R1,R2 şi R3. Nu putem însă împărţi cei 9 volţi la 3kΩ, 10kΩ sau 5kΩ pentru a găsi valoarea curentului, pentru că nu cunoaştem defapt valoarea tensiunii pe fiecare din rezistori în parte, cunoaştem valoarea tensiunii pe întreg ansamblul de rezistori doar.

Valoarea de 9 volţi reprezintă o cantitate totală din circuit, pe când valorile de 3kΩ, 10kΩ şi 5kΩ, reprezintă cantităţi individuale din cadrul circuitului de faţă. Dacă ar să folosim în cadrul legii lui Ohm o valoare totală (tensiunea în acest caz) concomitent cu o valoare individuală (rezistenţa în acest caz), rezultatul nu va fi acelaşi pe care îl vom regăsi într-un circuit real.
În cazul lui R1, legea lui Ohm se va folosi specificând tensiunea şi curentul la bornele rezistorului R1, şi valoarea rezistenţei lui, 3kΩ:

Dar din moment ce nu cunoaştem tensiunea la bornele lui R1 (doar tensiunea totală pe toţi cei trei rezistori conectaţi în serie), şi nu cunoaştem nici curentul prin R1 (curentul prin întreg circuitul defapt, deci şi prin ceilalţi doi rezistori), nu putem realiza niciun calcul cu niciuna dintre formule. Acelaşi lucru este valabil şi pentru R2 şi R3.
Prin urmare, ce putem face? Dacă am cunoaşte valoarea totală a rezistenţei din circuit, atunci am putea calcula valoarea totală a curentului pentru cantitatea totală a tensiunii (I=E/R).
Cu această observaţia putem enunţa al doilea principiu al circuitelor serie: în oricare circuit serie, rezistenţa totală a circuitului este egală cu suma rezistenţelor individuale a fiecărui rezistor, prin urmare, cu cât avem mai multe rezistenţe în circuit, cu atât mai greu le va fi electronilor să se deplaseze prin circuit. În exemplul nostru, aveam trei rezistori în serie, de 3 kΩ, 10 kΩ, respectiv 5 kΩ, ceea ce rezultă într-o rezistenţă totală de 18Ω:
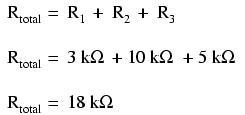
Ceea ce am făcut de fapt, a fost să calculăm rezistenţa echivalentă a rezistenţelor de 3 kΩ, 10 kΩ şi 5 kΩ luate împreună. Cunoscând acest lucru, putem redesena circuitul cu un singur rezistor echivalent reprezentând combinaţia serie a celor trei rezistori R1, R2 şi R3:
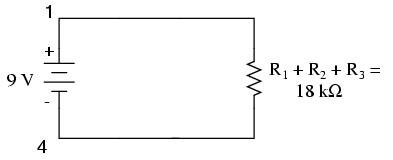
Acum avem toate informaţiile necesare pentru a calcula curentul prin circuit, deoarece aven tensiunea între punctele 1 şi 4 (9 volţi), precum şi rezistenţă între punctele 1 şi 4 (18kΩ):
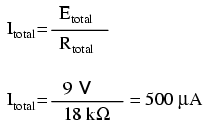
Cunoscând faptul că prin fiecare component în cadrul unui circuit serie, curentul este acelaşi, şi cunoscând valoarea acelui curentu în cazul de faţă, putem merge înapoi la circuitul iniţial şi să notăm valoarea curentului prin fiecare component în parte:
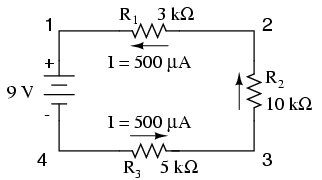
Acum că valoarea curentului prin fiecare rezistor ne este cunoscută, putem folosi legea lui OHm pentru determinarea căderilor de tensiune pe fiecare component în parte:
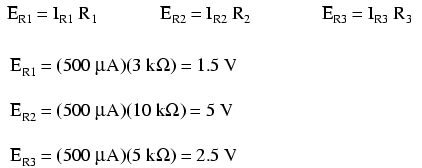
Putem observa căderea te tensiune pe fiecare rezistor în parte şi faptul că suma acestor căderi de tensiune (1.5 V + 5 V + 2.5 V) este egală cu tensiunea la bornele bateriei, 9 V. Acesta reprezintă al treilea principiu al circuitelor serie: tensiune electromotoare (a bateriei) este egală cu suma căderilor de tensiune pe fiecare component în parte.
5.3 Circuite paralel simple
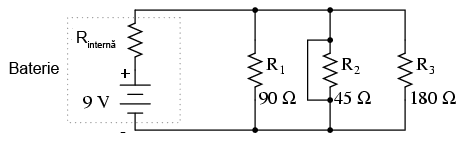
Să începem cu un circuit paralel format din trei rezistori şi o singură baterie:
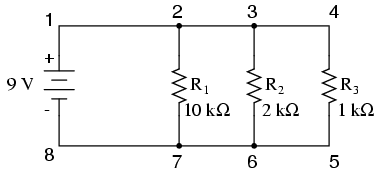
Primul principiu pe care trebuie să-l înţelegem despre circuitele paralele este legat de faptul că tensiunea este egală la bornele tuturor componentelor din circuit. Acest lucru se datorează existenţei a unui număr de numai două seturi de puncte comune din punct de vedere electric într-un circuit paralel, iar tensiunea măsurată între seturi de puncte comune trebuie să fie tot timpul aceeiaşi. Prin urmare, în circuitul de mai sus, tensiunea la bornele rezistorului R1 este egală cu tensiunea la bornele rezistorului R2egală cu tensiunea (căderea de tensiune) la bornele rezistorului R3 şi de asemenea egală cu tensiunea (electromotoare) la bornele bateriei.
Ca şi în cazul circuitelor serie, dacă dorim aplicarea legii lui Ohm, valorile tensiunii, curentului şi ale rezistenţei trebuie să fie în acelaşi context (total sau individual) pentru a obţine rezultate reale prin aplicarea formulelor. Totuşi, în circuitul de mai sus, putem aplica de la început legea lui Ohm fiecărui rezistor în parte, pentru că se cunoaşte tensiunea la bornele fiecărui rezistor (9 voloţi) precum şi rezistenţa fiecărui rezistor:

Până în acest moment, nu cunoaştem valoarea totală a curentului, sau rezistenţă totală a acestui circuit paralel, asfel că nu putem aplica legea lui Ohm pentru a afla valoarea totală a curentului prin circuit (între punctele 1 şi 8 de exemplu). Totuşi, putem observa că valoarea totală a curentului prin circuit trebuie să fie egală cu suma valorilor curenţilor prin fiecare ramură (fiecare rezistor în parte):
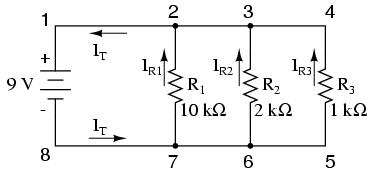
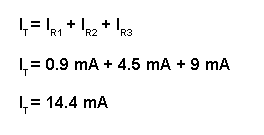
Pe măsură ce curentul iese prin terminalul negativ (-) al bateriei la punctul 8 şi se deplasează prin circuit, o parte din această cantitate se împarte în două la punctul 7, o parte mergând spre R1. La punctul 6 o parte din cantitate se va întrepta spre R2, iar ceea ce mai rămâne va curge spre R3. Acelaşi lucru se întâmplă pe partea cealaltă , la punctele 4, 3 şi 2, numai că de această dată curenţii se vor aduna şi vor curge împreună spre terminalul pozitiv al bateriei (+), la punctul 1. Cantitatea de electroni (curentul) ce se deplasează din punctul 2 spre punctul 1 trebuie să fie egală cu suma curenţilor din ramurile ce conţin rezistorii R1, R2 şi R3.
Acesta este al doilea principiu al circuitelor paralele: valoarea totală a curentului prin circuit este egală cu suma curenţilor de pe fiecare ramură în parte.
Şi în sfârşit, aplicând legea lui Ohm pe întreg circuitul, putem calcula valoarea totală a rezistenţei prezentă în circuit:
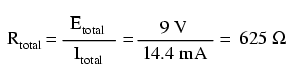
Trebuie să observăm un lucru foarte important în acest caz! Valoarea rezistenţei totale este de numai 625 Ω: mai puţin decât valoarea oricărei rezistenţe luate separat. În cazul circuitelor serie, unde rezistenţa totală este egală cu suma tuturor rezistenţelor individuale, suma totală a fost mai mare decât valoarea oricărei rezistenţe luate separat. În cadrul circuitelor paralel, este exact invers. Acesta este al doilea principiu al circuitelor electrice paralele, iar matematic, această relaţie între rezistenţa totală şi rezistenţele individuale din circuit poate fi exprimată astfel:
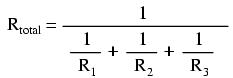
5.4 Conductanţa
Prin definiţie, rezistenţa este mărimea ce măsoară frecarea întâmpinată de electroni atunci când se deplasează prin componentul respectiv (rezistor). Totuşi, putem să ne gândim şi la inversa aceasei mărimi electrice: cat de uşor le este electronilor să se deplaseze printr-un component, faţă de cât de dificil, cum este cazul rezistenţei. Denumirea pentru această uşurinţă este conductanţa electrică, în opoziţie cu rezistenţa electrică.
Matematic, conductanţa este inversa rezistenţei:
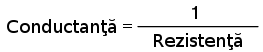
Cu cât valoarea rezistenţei este mai mare, cu atât mai mică va fi cea a conductanţei şi invers. Simbolul folosit pentru desemnarea conductanţei este „G”, iar unitatea de măsură este siemens, abreviat prin „S”.
Întorcându-ne la circuitul paralel studiat, putem vedea că existenţa mai multor ramuri în circuit reduc rezistenţa totală a circuitului, pentru că electroni sunt capabil să curgă mult mai uşor prin circuit atunci când există mai multe ramuri decât atunci când există doar una. În termeni de rezistenţă, ramurile îm plus rezultă într-o rezistenţă mai scăzută. Dacă folosim însă termenul de conductanţă, ramurile adiţionale din circuit duc la o conductanţă (totală) mai mare.
Rezistenţa totală paralelă este mai mică decât oricare dintre rezistenţele ramurilor luate individual (Rtotal mai mică decât R1, R2, R3 sau R4 luate individual):
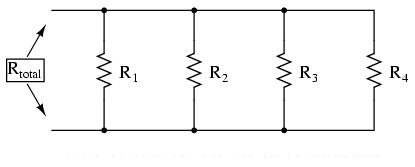
Conductanţa paralelă este mai mare decât oricare dintre conductanţele ramurilor luate individual, deoarece rezistorii paraleli conduct mai bine curantul electricât decât o fac fiecare luat în parte(Gtotal mai mare decât G1, G2, G3 sau G4 luate individual):
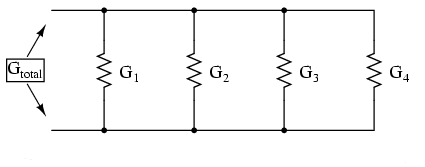
Matematic, această relaţie se exprimă asfel:
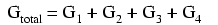
Cunoscând relaţia matematică inversă dintre conductanţă şi rezistenţă (1/x), putem transforma fiecare din termenii formulei de mai sus în rezistenţe:
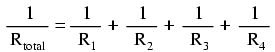
Rezolvând ecuaţie de mai sus pentru Rtotal, ajungem la următoarea formulă:
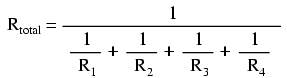
Asfel, ajungem la formula rezistenţei totale dintr-un circuit paralel.
5.5 Calcularea puterii
La calcularea puterii disipate pe componentele rezistive, putem folosi oricare dintre ecuaţiile de putere în funcţie de mărimile cunoscute: tensiune, curent şi/sau rezistenţă pe fiecare componentă.
P = IE, P = E2 / R, P = I2R
Acest lucru este mult mai uşor de realizat prin simpla adăugare a unui rând adiţional în tabelul tensiunilor, curenţilor şi rezistenţelor.
| Marime | R1 | R2 | R3 | Total | Unitate |
|---|---|---|---|---|---|
| E | V | ||||
| A | I | ||||
| R | Ω | ||||
| P | W |
Indiferent de coloană, puterea se va afla folosind ecuaţia corespunzătoare a legii lui Ohm.
O regulă interesantă pentru puterea totală vizavi de puterea individuală, este că aceasta este aditivă indiferent de configuraţia circuitului în cauză: serie, paralel, serie-paralel sau altfel. Fiind o expresie a lucrului mecanic efectuat, puterea configuraţia circuitului nu are niciun efect asupra calculelor matematice dacă luăm în considerare şi faptul că puterea disipată trebuie să fie egală cu puterea totală introdusă de către sursă în circuit (conform legii conservării energiei).
Atenţie, cele de mai sus se aplică doar în cazul calculării puterilor în circuitele pur rezistive (ce conţin doar rezistori).
5.6 Aplicarea corectă a legii lui Ohm
Una dintre cele mai frecvente greşeli ale începătorilor în aplicarea legii lui Ohm constă în utilizarea greşită a mărimilor pentru tensiune, curent şi rezistenţa. Cu alte cuvinte, se poate întâmpla ca în aplicarea legii să se utilizeze valoarea curentului I printr-un rezistor şi valoarea căderii de tensiune U (sau E) pe un set de rezistori interconectaţi, cu speranţa că rezistenţa totală astfel calculată este egală cu rezistenţa reala a configuraţiei în cauză. Acest lucru este însă incorect! Reţineţi acest principiu extrem de important: variabilele utilizate în ecuaţiile legii lui Ohm trebuie să corespundă tot timpul aceluiaşi set de două puncte a circuitului în cauză. Cu alte cuvinte, dacă luăm în considerare o rezistenţă RAB aflată între două puncte din circuit, desemnate prin A şi B, atunci şi curentul IAB cât şi căderea de tensiune UAB trebuie să se refere exact la aceleaşi puncte pentru a putea aplica corect legea lui Ohm. Această observaţie este extrem de importantă în special în circuitele combinate serie-paralel, acolo unde componente adiacente pot avea valori diferita atât pentru tensiune cât şi pentru curent.
Utilizând metoda tabelului, putem să ne asigurăm de aplicarea corectă a legii lui Ohm considerând ca şi coloane doar rezistori individuali şi nu set de rezistori conectaţi în combinaţii serie, paralel sau serie-paralel. Vom folosi această metodă mai târziu pentru rezolvarea unor circuite mai complicate.
| Marime | R1 | R2 | R3 | Total | Unitate |
|---|---|---|---|---|---|
| E | V | ||||
| I | A | ||||
| R | Ω | ||||
| P | W |
Astfel, în cazul circuitelor serie, coloana total poate fi foarte uşor calculată utilizând regulile circuitelor serie, şi anume: căderea totală de tensiune este egală cu suma căderilor individuale pe fiecare component, curentul total este egal cu valoarea curentului prin oricare component, rezistenţa totală este egală cu suma rezistenţelor individuale, iar puterea totală este şi ea egală cu suma puterilor individuale.
Pentru circuitele serie, coloana total se calculează astfel: căderea de tensiune totală este aceiaşi cu tensiunea de pe fiecare component, curentul total este egal cu suma curenţilor individuali, rezistenţa totală se calculează cu formula rezistenţei totale a circuitelor parale, iar puterea totală este egală cu suma puterilor individuale.
5.7 Analiza circuitelor defecte
Sarcina unui tehnician presupune adesea localizarea şi remedierea sau înlocuirea componentelor dintr-un circuit defect. Identificarea componentelor defecte presupune un efort considerabil, necesitând o foarte bună înţelegere a principiilor de bază, abilitatea de a formula ipoteze, de a judeca valoare acestora bazându-se pe probabilităti şi un simt al creactivitâţii în aplicarea unei soluţii pentru remedierea problemei. Deşi este posibilă trasarea unor metode ştiinţifice în jurul acestor abilităţi, majoritatea tehnicienilor cu experienţă văd această activitate ca pe o artă ce necesită ani de experienţă.
O abilitate esenţială este înţelegerea rapidă şi intuitivă a modului în care defectarea componentelor afectează comportamentului circuitului în ansamblul său, indiferent de configuraţia acestuia. Vom explora unele dintre aceste efecte atât în cazul circuitelor serie cât şi în cazul circuitelor paralel.
5.7.1 Analiza defectelor într-un circuit serie simplu
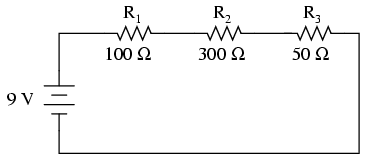
Să considerăm circuitul alăturat
| Marime | R1 | R2 | R3 | Total | Unitate |
|---|---|---|---|---|---|
| E | 2 | 6 | 1 | 9 | V |
| I | 20 m | 20 m | 20 m | 20 m | A |
| R | 100 | 300 | 50 | 450 | Ω |
Atunci când toate componentele acestui circuit funcţionează la parametrii normali, putem determina pe cale matematică toţi curenţi şi căderile de tensiune din circuit.
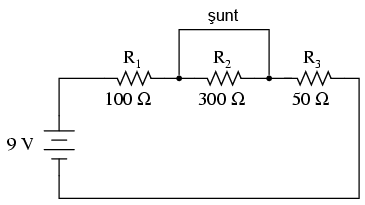
Să presupunem acum că rezistorul R2 este scurt-circuitat; acest lucru înseamnă de fapt că, în locul rezistorului avem un simplu fir ce prezintă o rezistenţa aproape nulă. Practic, în circuitul alăturat, spunem că am realizat o şuntare a rezistorului R2 iar firul utilizat poartă numele de conductor de şuntare, sau simplu, şunt.
| Marime | R1 | R2 | R3 | Total | Unitate |
|---|---|---|---|---|---|
| E | 6 | 0 | 3 | 9 | V |
| I | 60 m | 60 m | 60 m | 60 m | A |
| R | 100 | 0 | 50 | 150 | Ω |
Odată cu scurt-circuitarea rezistorului R2, fie prin şuntarea intenţionată a acestuia fie printr-un defect intern, valoarea rezistenţei totale din circuit va fi mai mică. Din moment ce tensiunea la bornele bateriei rămâne aceiaşi, o scăderea a rezistenţi totale din circuit conduce la creşterea curentului total.
Odată cu creşterea curentului de la 20 mA la 60 mA, căderea de tensiune pe rezistorii R1 şi R3 (a căror rezistenţă nu s-a modificat) creşte şi ea, astfel încât căderea de tensiune totală pe cele două componente rămase să fie tot 9 V. Rezistorul R2, fiind şuntat de rezistenţa foarte mică a conductorului de şuntare, este practic eliminat din circuit, rezistenţa dintre cele două captele ale conductorului fiind practic zero. Din această cauză, căderea de tensiune pe rezistorul R2 este de zero V, chiar dacă valoarea totală a curentului din circuit a crescut.
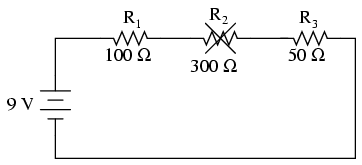
Pe de altă parte, dacă defectul suferit de rezistorul R2 este de aşa natură încât circuitul va rămâne deschis în acel punct - rezistenţa între cele două captele libere ale conductorilor rămaşi creşte practic spre infinit - efectele asupra circuitului iniţial vor fi diferite, dar la fel de radicale.
| Marime | R1 | R2 | R3 | Total | Unitate |
|---|---|---|---|---|---|
| E | 0 | 9 | 0 | 9 | V |
| I | 0 | 0 | 0 | 0 | A |
| R | 100 | ∞ | 50 | ∞ | Ω |
Cu R2 având o rezistenţă infinită, iar rezistenţa totală într-un circuit serie fiind dată de suma tuturor rezistenţelor individuale, rezistenţa totală creşte spre infinit iar curentul total la zero. În această situaţie, nu va mai exista nicio deplasare a electronilor prin circuit necesară producerii unor căderi de tensiune pe rezistorii R1 sau R3. În schimb, întreaga cădere de tensiune dezvoltată de baterie se va regăsi pe terminalele rezistorului R2.
5.7.2 Analiza defectelor într-un circuit paralel simplu
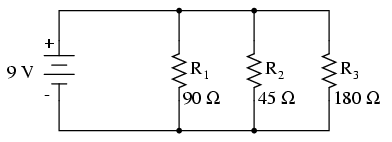
Putem aplica aceleaşi metode şi în cazul unui circuit paralel.
| Marime | R1 | R2 | R3 | Total | Unitate |
|---|---|---|---|---|---|
| E | 9 | 9 | 9 | 9 | V |
| I | 100 m | 200 m | 50 m | 350 m | A |
| R | 90 | 45 | 180 | 25,71 | Ω |
Să observăm prima dată comportamentul unui circuit paralel „sănătos”.
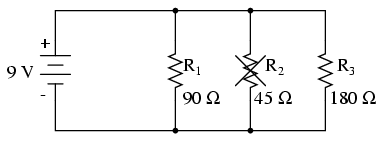
- Înlăturarea rezistorului
Să presupunem acum deschiderea rezistenţei R2 în acest circuit paralel.
Marime R1 R2 R3 Total Unitate E 9 9 9 9 V I 100 m 0 50 m 150 m A R 90 ∞ 180 60 Ω Efectele acestui defect le putem observa în tabelul alăturat.
În cazul acestui circuit paralel, deschiderea unei ramuri afectează doar curentul prin acea ramură precum şi curentul total dincircuit. Căderea de tensiune, fiind egală pe toate componentele va rămâne neschimbată pe toţi rezistorii. Datorită tendinţei sursei de alimentare de menţinere constantă a tensiunii de alimentare, aceasta nu se va modifica, şi datorită faptului că este conectată în paralel cu toţi rezistorii, căderea de tensiune pe fiecare dintre ei, după apariţia defectului, rămâne egală cu 9 V. Din această cauză (rezistenţa constantă, căderea de tensiune constantă) curentul prin ceilalţi doi rezistori nu se modifică nici ei.
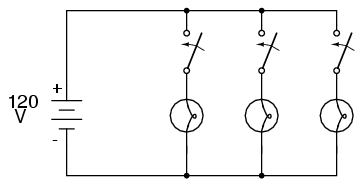
Acelaşi lucru îl putem observa şi într-un circuit casnic: toate becurile sunt conectate în paralel. La pornirea sau oprirea unui bec (o ramură din circuitul paralel se închide şi se deschide), funcţionarea celorlalte becuri nu este afectată; singurul lucru care se modifică este curentul prin acel bec (circuit de ramură) şi curentul total din circuit.
- Şuntarea rezistorului
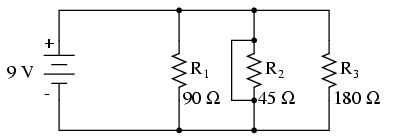
Într-un caz ideal (surse de tensiune perfecte şi conductori cu rezistenţă zero), rezistorii scurt-circuitaţi dintr-un circuit paralel simplu nu vor avea niciun efect asupra comportamentului celorlalte ramuri din circuit. În realitate însă, efectul nu este acelaşi, după cum putem observa din exemplul alăturat.
Marime R1 R2 R3 Total Unitate E 9 9 9 9 V I 100 m ∞ 50 m ∞ A R 90 0 180 0 Ω Un rezistor scurt-circuitat (rezistenţa de 0 Ω) va permite, teoretic, trecerea unui curent infinit de la oricare sursă finită de tensiune (I = E / 0). În acest caz, rezistenţa nulă a rezistorului R2 descreşte rezistenţa totală a circuitului la zero Ω, ducând la creşterea valorii curentului spre infinit. Atâta timp cât tensiunea sursei rămâne constantă la 9 V, curenţii prin celelalte ramuri ale circuitului (IR1 şi IR3) rămân neschimbaţi.
Ipoteza critică pe care ne-am asumat-o în această situaţie este că tensiunea de alimentare rămâne constantă pentru un curent infinit introdus în circuit. Acest lucru nu este însă deloc realist. Chiar dacă scurt-circuitul prezintă o rezistenţa mică (faţă de o rezistenţa egală cu zero), nicio sursă reală de tensiune nu poate genera un supra-curent extrem de mare în acelaşi timp cu menţinerea valorii tensiunii la un nivel constant.
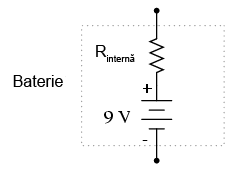
Acest lucru se datorează rezistenţei interne caracteristice tuturor surselor de putere electrice, rezistenţe datorate proprietătilor intrinseci ale materialelor din care sunt construite.
Aceste rezistenţe interne, oricât de mici, transformă circuitul paralel de mai sus într-o combinaţie serie-paralel. De obicei, rezistenţele interne al surselor de putere sunt suficient de mici pentru a putea fi ignorate fără nicio problemă, dar odată cu apariţia curenţilor foarte mari datorită componentelor scurt-circuitate, efectelor lor nu mai pot fi neglijate. În acest caz, scurt-circuitarea rezistenţei R2 va duce la situaţia în care întreaga cădere de tensiune se va regăsi pe rezistenţa internă a bateriei, căderile de tensiune pe R1, R2 şi R3 fiind aproape zero.
Marime R1 R2 R3 Total Unitate E mică mică mică mică V I mic mare mic mare A R 90 0 180 0 Ω Ca şi concluzie, scurt-circuitarea intenţionată a terminanilor surselor de alimentare, indiferent de tipul acestora, trebuie evitată cu orice preţ. Chiar şi în cazul în care curenţii mari dezvoltaţi (căldură, scântei, explozii) nu duc la rănirea niciunei persoane din apropiere, sursa de tensiune va suferi cu siguranţă unele defecte în cazul în care nu este proiectată a rezista la curenţi de scurt-circuit (majoritatea surselor de tensiune nu sunt).
5.8 Construirea circuitelor rezistive simple
Pe măsură ce studiaţi circuitele electrice, veţi dori probabil să construiţi propriile circuite utilizând baterii şi rezistori (becuri, de exemplu). Există câteva opţiuni pentru realizarea acestor circuite, unele mai simple decât altele, opţiuni pe care le vom prezenta în acest capitol.
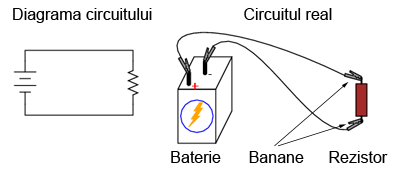
Dacă dorim realizarea unui circuit simplu cu o sigură baterie şi un singur rezistor, putem foarte bine să utilizăm conductori cu cleme (crocodil/banană).
Astfel de conductori, prevăzuţi cu banane pe la capete, reprezintă o metodă practică şi sigură din punct de vedere electric pentru conectarea componentelor între ele.
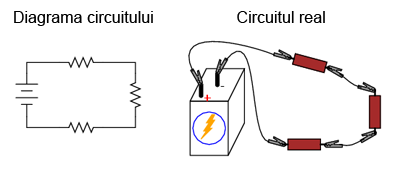
Dacă am dori să realizăm un circuit simplu cu o baterie şi trei rezistor, putem utiliza aceiaşi metodă de conectare a conductorilor.

Totuşi, această tehnică se dovedeşte a nu fi practică atunci când avem de a face cu circuite mult mai complicate decât cele de mai sus. O metodă mult mai practică de realizare a circuitelor temporare este utilizarea unei plăci de test (solderless breadboard), un dispozitiv realizat din plastic ce permite realizarea uşoară a unui număr relativ mare de conexiuni între componente.
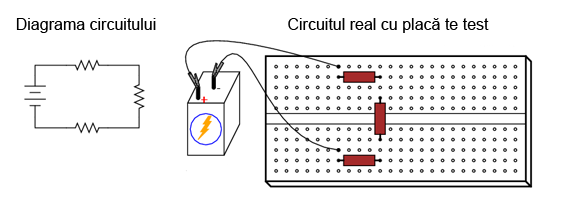
Alăturat este un exemplu de circuit realizat cu ajutorul plăcii de test.
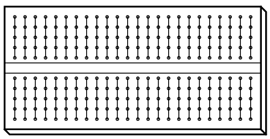
Sub fiecare cavitate există un arc metalic ce prinde orice conductor sau terminal al componentelor introduse în acesta. Aceste arcuri metalice sunt conectate între ele pe spatele plăcii, realizâd astfel conexiuni între conductorii inseraţi prin partea superioară. Modelul plăcii este astfel încât, există o serie de cinci astfel de cavităţi unite vertical între ele, conform figurii alăturate.
Astfel că atunci când inserăm un conductor într-una dintre cavităţi, există încă o serie de patru astfel de cavităţi pe aceeiaşi coloană, ce sunt comune din punct de vedere electric cu prima. Introducerea unui terminal sau conductor în oricare dintre aceste puncte comune este identică din punct de vedere electric cu conectarea directă a terminalilor sau conductorilor celor două componente. Rezultatul este o platformă extrem de flexibilă pentreu realizarea circuitelor electrice sau electronice temporare.
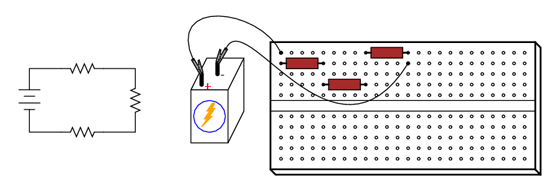
De exemplu, circuitul electric de mai sus, format din trei rezistori, poate fi construit cu ajutorul unei plăci de test conform figurii alăturate.
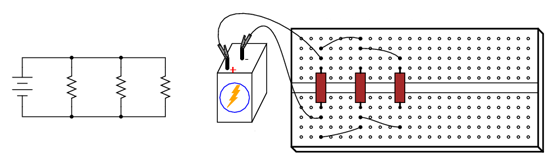
Un alt exemplu, de această dată a unui circuit paralel cu trei rezistori, este prezentat în figura alăturată.
Acest plăci de test au totuşi unele neajunsuri. În primul rând, scopul lor sunt doar circuitele temporare. Dacă întoarcem placa şi o scuturăm, componentele s-ar putea să cadă din locaţiile lor respective. De asemenea, plăcile sunt limitate la curenţi destul de mici (sub 1 A). Acele arcuri metalice au o suprafaţă de contact destul de mică, prin urmare, nu pot suporta curenţi mari fără încălzirea lor excesivă.
5.8.1 Regleta de conexiuni
O metodă alternativă constă în utilizarea unei reglete de conexiuni (regletă de borne). Acestea sunt compuse dintr-un material izolator prevăzut cu spaţii metalice pentru prinderea conductorilor cu ajutorul unor şuruburi; acest procedeu este similor modului de conectare al prizelor sau întrerupătoarelor casnice.

Un exemplu de astfel de regletă, având o serie de conductori ataşaţi, este prezentat în poza alăturată.

O altă variantă este cea din poza alăturată. Această variantă, denumită şi „europeană” are şuruburile introduse într-un canal pentru a preveni scurt-circuitarea accidentală între terminali prin intermediul unei şurubelniţi sau al unui alt obiect metalic.
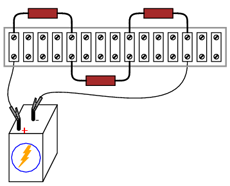
În figura alăturată, este prezentat un circuit serie compus dintr-o singură baterie şi trei rezistori folosind o regletă de conexiuni.
Conxiunile realizate cu ajutorul unei reglete sunt robuste şi pot fi prin urmare folosite atât pentru circuitele temporare cât şi pentru construcţia circuitelor permanente.
Una dintre deprinderile esenţiale ale celor care vor să pună în practică lecţiile învăţate despre circuitele electrice şi electronice, este „traducerea” unei diagrame într-un circuit real. Diagramele circuitelor sunt de obicei realizate pentru a facilita citirea lor cu uşurinţă, dar circuitele practice au de cele mai multe ori o orientare complet diferită.
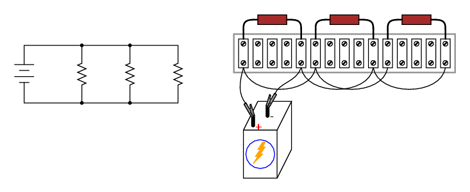
Să luăm ca şi exemplu un circuit paralel format dintr-o singură baterie şi trei rezistori.
Trecerea de la o diagrama circuitului la realizarea propriu-zisă a acestuia - mai ales atunci când rezistori ce trebuie conectaţi sunt aranjaţi liniar (asemănător circuitelor serie, nu paralel) pe regletă - nu este chiar aşa de evidentă, prin urmare, vom prezenta procesul pas cu pas în cele ce urmează.
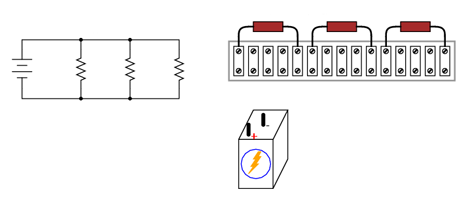
Pentru început, considerăm diagrama iniţială a circuitului şi toate componentele prinse pe regleta de conexiuni dar fără niciun conductor electric între ele.
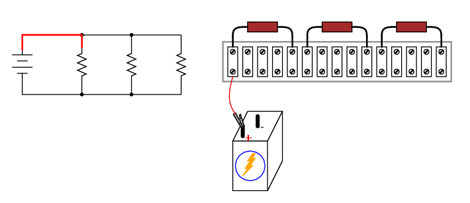
Apoi, urmărim conductorul dinspre terminalul pozitiv al bateriei spre primul component al diagramei, realizând în acelaşi timp o legătură fizică, prin intermediul unui conductor, între aceste două puncte pe circuitul real. Dacă ne este mai uşor, putem trasa o linie de o culoare diferită pe diagramă, pentru a reprezenta ce tip de conexiuni au fost deja realizate în circuitul real.
Continuând acest proces, fir cu fir, până în momentul în care întreaga schemă electrică (diagramă) a circuitului este acoperită.
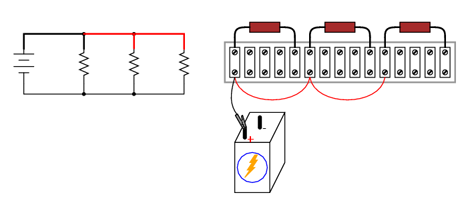
Următorul pas, aşadar, constă în conectarea bornelor superioare a celor doi rezistori rămaşi.
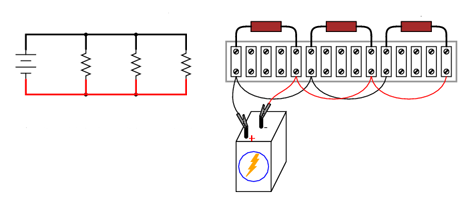
Având toate bornele superioare ale tuturor rezistorilor din circuit conectate la borna pozitivă a bateriei, următorul pas este să conectăm bornele inferioare ale acestora la borna negativă a bateriei.
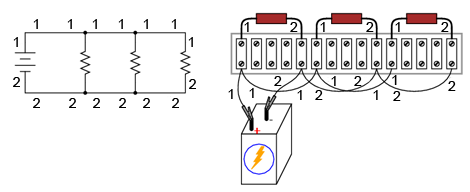
În mod normal, în circuitele practice folosite în industrie, toate firele sunt marcate; conductorii comuni din punct de vedere electric posedă acelaşi număr de marcaj. În exemplu nostru, am marcat conductorii cu 1 şi 2.
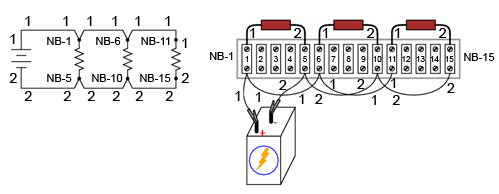
O altă convenţie constă în modificarea uşoară a diagramei iniţiale pentru a indica punctul de contact propriu-zis al conductorului pe regletă. Acest lucru necesită un sistem de marcaj al regletei: „NB” (numărul blocului), si un număr reprezentând fiecare conexiune metalică de pe regletă.
În acest mod, diagrama poate fi utilizata ca şi o „hartă” pentru localizarea punctelor dintr-un circuit real, indiferent cât de încâlcit şi de complex este în realitate. Această metodă poată părea exagerată pentru circuitul simplu cu trei rezistori de mai sus, dar aceste detalii sunt absolut necesare pentru realizarea şi întreţinerea circuitelor mari, în special ale acelora care se intind pe o distanţă considerabilă, folosind mai multe relgete localizate în puncte diferite.
Pentru circuite permanente, se pot folosi plăci imprimate, un subiect destul de vast în ale cărui detalii nu vom intra aici.