< Curent continuu

13 Condensatorul

13.1 Câmpuri şi capacitatea electrică

Atunci când între doi conductori există o tensiune electrică, spunem că există un câmp electric în spaţiul dintre ei. Vorbind de câmpuri ne referim de fapt la interacţiunile ce au loc în spaţiul dintre şi din jurul conductorilor şi nu în interiorul acestora.

Conceptul de „câmp” este cu siguranţă unul destul de abstract. Cel puţin în cazul curentului electric ne putem imagina, fără prea mare dificultate, existenţa unor particule minuscule, denumite electroni, ce se deplasează între atomii conductorilor. Dar un „câmp” nu are nici măcar masă şi poate să nu existe deloc în materie.

În ciuda aspectului abstract, putem da un exemplu destul de practic cu care majoritatea dintre noi suntem familiarizaţi, şi anume magneţii. Deşi aparent nu există nicio legătură directă între două bucăţi separate de magnet, există cu siguranţă o forţă de atracţie sau de respingere în funcţie de orientarea lor relativă. Această „forţă” nu are nici culoare, nici masă, nici miros, iar dacă nu am observa interacţiunile dintre ei, nici nu am ştii că există. În cadrul fizicii, interacţiunile ce au loc în spaţiul dintre magneţi poartă numele de câmpuri magnetice. Dacă plasăm pilitură de fier în jurul unui magnet, putem oberva (re)orientarea acesteia în jurul liniilor de câmp; în acest fel putem avea o indicaţie vizuală a prezenţei câmpului magnetic.

Subiectul acestui capitol sunt câmpurile electrice (şi condensatoarele ce utilizează acest principiu) nu câmpurile magnetice, dar există multe asemănări între cele două. Mai mult ca sigur că sunteţi familiarizaţi şi cu câmpurile electrice. Un exemplu a fost dat îm primul capitol, atunci când am explicat electricitatea statică şi modul în care materiale precum parafina şi lâna se atrag după ce au fost în prealabil frecate una de cealaltă. Din nou, fizicienii includ aceste interacţii în domeniul câmpurilor electrice generate de două corpuri ca rezultat al dezechilibrului de electroni dintre ele. Este suficient să spunem că prezenţa unei diferenţe de potenţial (tensiuni) dintre două puncte duce la apariţia unui câmp electric în spaţiul rămas liber dintre acestea.

Câmpurile au două caracteristici principale: forţa şi fluxul. Forţa reprezintă cantitatea de „împingere” pe care un câmp îl exercită la o anumită distanţă. Fluxul este cantitatea totală, sau efectul, câmpului prin spaţiu. Forţa şi fluxul câmpului sunt aproximativ similare tensiunii (împingere) şi curentului (curgere) printr-un conductor. Fluxul unui câmp poate întâmpina rezistenţă în spaţiu precum un curent întâmpină rezistenţă într-un conductor. Cantitatea fluxului dezvoltat în spaţiu este proporţională cu valoarea forţei aplicate împărţită la valoarea opoziţiei fluxului. În cazul curentului, tipul de material conductor determină rezistenţa specifică la curgerea acestuia; similar, în cazul fluxului, tipul materialului dielectric (izolator) ce separă cele două conductoare determină opoziţia specifică.

În mod normal, electronii nu pot intra într-un conductor decât dacă există o cantitate egală de electroni ce părăsesc exact acelaşi conductor (analogia tubului cu mărgele). Din această cauză conductorii trebuie conectaţii împreună pentru a forma un drum complet (circuit) pentru deplasarea continuă a electronilor. Ciudat este totuşi faptul că, electroni adiţionali pot fi „îngrămădiţi” într-un conductor, fără existenţa unui drum de ieşire, dacă este posibilă/permisă formarea unui câmp electric în spaţiul liber dintre acest conductor şi un alt conductor. Numărul electronilor adiţionali din conductor (sau numărul de electroni pierduţi) este direct proporţional cu valoarea fluxului câmpului dintre cei doi conductori.

Condensatoarele sunt componente ce utlizează acest fenomen electric în funcţionarea lor. Acestea sunt realizate din două armături (plăci) metalice conductoare plasate una în apropierea celeilalte, separate printr-un dielectric. Există totuşi o multitudine de tipuri şi moduri de construcţia a condensatoarelor, în funcţie de aplicaţia necesară.

Simbolul electric al condensatorului este prezentat în următoarea figură:

Atunci când la bornele condensatorului aplicăm o tensiune electrică, între cele două armături ia naştere un câmp electric ce permite existenţa unei diferenţe semnificative de electroni liberi (sarcină) între cele două armături:

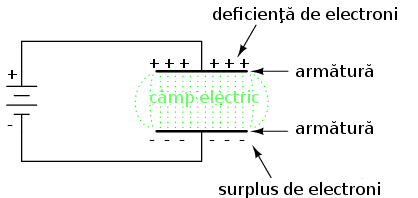
Pe măsură ce câmpul electric este format prin aplicarea tensiunii, electronii liberi vor fi forţaţi să se „adune” la terminalul negativ fiind „furaţi” de pe terminalul negativ. Acestă diferenţă de sarcină se traduce prin apariţia unui stoc de energie electrică în condensator şi reprezintă sarcina potenţială a electronilor dintre cele două armături. Cu cât diferenţa numerică a electronilor între cele două armături ale unui condensator este mai mare, cu atât mai mare este fluxul câmpului şi cu atât mai mare „stocul” de energie din condensator.

Deoarece condensatorii stochează energie potenţială sub formă de câmp electric, comportamentul lor într-un circuit este fundamental diferit de cel al rezistorilor, cei din urmă disipând pur şi simplu putere în circuit sub formă de căldură. Energia stocată într-un condensator depinde de tensiunea dintre armături precum şi de alţi factori pe care îi vom lua imediat în considerare. Abilitatea acestora de stocare a energiei în funcţie de tensiune rezultă într-o tendinţă de menţinere a tensiunii la un nivel constant. Cu alte cuvinte, condensatoarele tind să se opună variaţiei căderii de tensiune. Atunci când modificăm tensiunea la bornele unui condensator, fie o mărim, fie o scădem, acesta tinde să se opună schimbării trăgând curent de la sau generând curent spre sursa de variaţie a tensiunii, în opoziţie cu variaţia.

Pentru a stoca mai multă energie într-un condensator, trebuie mărită valoarea tensiunii la bornele sale. Acest lucru prsupune o înmulţire a electronilor pe armătura negativă şi o diminuare a lor pe cea negativă, lucru ce necesită existenţa unui curent în acea direcţie. Dimpotrivă, pentru a elibera energie dintr-un condensator, trebuie scăzută valoarea tensiunii la bornele sale. Acest lucru presupune o diminuare a electronilor pe armătura negativă prin deplasarea lor spre cea pozitivă; această deplasare dă naştere, evident, unui curent în acea direcţie (opusă).

Asemenea legii de mişcare a lui Isaac Newton (un obiect aflat în mişcare, tinde să rămână în mişcare; un obiect aflat în repaus tinde să rămână în repaus) ce descrie tendinţa obiectelor de a se opune variaţiilor de viteză, putem descrie tendinţă unui condensator de a se opune variaţiei tensiunii asfel: „Un condensator încărcat tinde să rămână încărcat; un condensator descărcat tinde să rămână descărcat.” Ipotetic, un condesator (încărcat sau descărcat) lasat neatins îşi va menţine la infinit starea sa iniţială. Doar o sursă (sau un canal) exterior de curent poate modifica valoarea energiei stocate (implicit şi a tensiunii la bornele sale) de un condensator perfect:

Practic, condensatoarele îşi vor pierde tensiune stocată datorită imperfecţiunilor interne ce permit electronilor să se deplaseze de pe o armătură pe cealaltă. În funcţie de tipul specific de condensator, timpul de „golire” poate fi foarte lung, de până la câţiva ani, pentru condensatoarele ce nu sunt deloc folosite.

Când tensiune la bornele condensatorului creşte, acesta trage curent din circuit; în acest caz condensatorul se comportă ca o sarcină şi spune că se încarcă. Observaţi direcţia de deplasare a electronilor (curentul) faţă de polaritatea tensiunii:

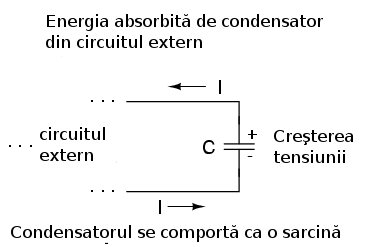
Invers, atunci când tensiunea la bornele condensatorului scade, acesta introduce/generează curent în circuitul extern; în acest caz condensatorul se comportă ca o sursă de putere şi spunem că se descarcă. Stocul de energie din câmpul electric este direcţionat către restul circuitului. Observaţi direcţia de deplasare a electronilor (curentul) faţă de polaritatea tensiunii:

Dacă introducem brusc o sursă de tensiune la bornele unui condensator descărcat (o creştere bruscă de tensiune), acest va trage curent din circuitul exterior, reprezentat în acest caz de sursa respectivă, până în momentul în care tensiune la bornele sale este egală cu tensiunea sursei. După atingerea acestui punct de încărcare, curentul scade spre zero (condensator încărcat). Invers, dacă o rezistenţă de sarcină este conectată la bornele unui condensator încărcat, acesta va genera curent spre sarcină până în momentul epuizării energiei stocate, iar tensiunea sa va scădea spre zero. După atingerea acestui punct de descărcare, curentul scade spre zero. Putem să ne gândim la condensatoare ca la un fel de baterii secundare prin modul de încărcare şi descărcare al lor.

Precum am mai spus, alegerea materialului izolant dintre plăci are o importanţă capitală în comportamentul condensatorului, mai bine spus, în mărimea fluxului electric şi implicit a tensiunii dintre armături. Datorită rolului acestui material în comportamentului fluxului, i s-a dat un nume special: dielectric. Nu toate materialele dielectrice sunt egale, ci sunt diferenţiate printr-o valoare fizică numită permitivitatea dielectricului.

Mărimea pentru volumul de energie stocat de un condensator, atunci când se aplică o anumită tensiune la bornele sale, poartă denumirea de capacitate. Simbolic, se notează cu „C” şi se măsoară în Farad, prescurtat „F”.

Există o anumită convenţie atunci când vine vorba de notaţia condensatoarelor, şi anume, valorile acestora se exprimă adesea în mircoFarad (µF).

Aparent, denumirea de condensator este învechită şi nu mai este folosită în lucrările de specialitate, fiind înlocuită cu cea de capacitor. Întrucât în literatura de specialitate de la noi din ţară se foloseşte încă termenul de condensator, îl vom folosi şi noi în această carte.

13.2 Relaţia tensiune-curent pentru condensator

Condensatorii nu au o „rezistenţă” stabilă precum am rezistorii. Totuşi, există o relaţie matematică precisă între tensiunea şi curentului unui condensator:

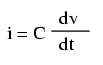
Litera „i” semnifică curentul instantaneu, adică valoarea curentului la un anumit moment din timp. Acest lucru este în contrast cu valoarea constantă a curentului, sau curentul mediu („I”) pe o perioadă de timp nedefinită. Expresia „dv/dt” aparţine analizei matematice şi semnifică rata de variaţia instantanee a tensiunii cu timpul, sau rata de variaţia a tensiunii (creştere sau descreştere în volt pe secundă) la un anumit moment în timp, acelaşi la care se referă şi curentul instantenu. Observaţi că notaţia tensiunii în acest caz este v şi nu e!

Până în acest moment nu am mai întâlnit variabila timp în studiul circuitelor electrice. Atunci când am vorbit de valori ale tensiunilor, curenţilor şi rezistenţelor rezistorilor, ne-a fost indiferent dacă măsurătorile au fost făcute pe o perioadă de timp nespecificată (E=IR; V=IR) sau la un anumit moment din timp (e=ir; v=ir). Formulele folosite sunt exact aceleaşi, şi asta pentru că timpul nu afectează valoarea tensiunii, a curentului sau a rezistenţei într-un component precum rezistorul.

În cazul unui condensator pe de altă parte, timpul este o variabilă esenţială, doarece curentul depinde de rapiditatea variaţiei tensiunii în timp. Pentru a înţelege pe deplin acest lucru, vom lua câteva exemple. Să presupunem că un condensator este conectat la o sursă de tensiune variabilă construită dintr-o baterie şi un potenţiometru:

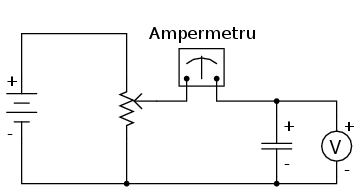
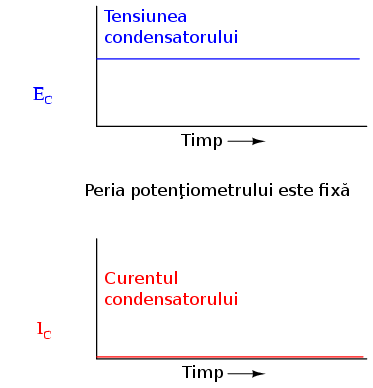
Dacă potenţiometrul rămâne în aceeiaşi poziţie (perie este fixă), voltmetrul conectat la bornele condensatorului va înregistra o tensiune constantă iar ampermetrul va înregistra 0 A. În acest caz, variaţia instantanee a tensiunii (dv/dt) este egală cu zero, deoarece tensiunea nu se modifică. Ecuaţia ne spune că având o rată de variaţie de 0 V / s pentru dv/dt, curentul instantaneu (i) trebuie să fie egal cu zero. Fizic, fără existenţa unei variaţii a tensiunii, nu este nevoie de nicio deplasare a electronilor de pe o armătură a condensatorului pe alta, şi prin urmare nu există nici curent.

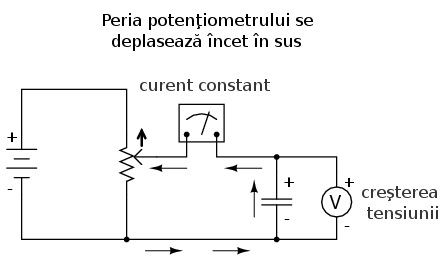
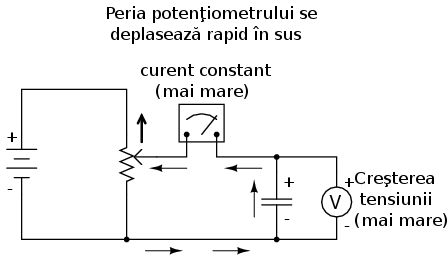
Dacă în schimb peria motenţiometrului se deplasează în mod constant în „sus” (spre borna pozitivă), căderea de tensiune pe condensator va fi din ce în ce mai mare. Voltmetrul înregistrează o creştere constantă a tensiunii indicate:

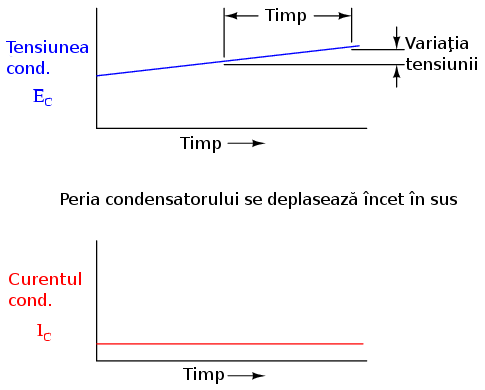
Dacă presupunem că deplasarea periei condensatorului în „sus” se realizează asfel încât există o rată constantă de creştere a tensiunii la bornele condensatorului (de ex., 2 volţi pe secundă), termenul dv/dt din formula de mai sus va avea o valoare fixă. Ecuaţia ne spune în acez caz că, valoarea fixă a lui dv/dt (2 V/s) înmulţită cu capacitatea condensatorului în Farad, de asemenea o valoare fixă, duce la o valoare fixă (constantă) a curentului. Fizic, o creştere a tensiunii la bornele condensatorului presupune o creştere a sarcinii diferenţiale (creşterea diferenţei numărului de electroni) între cele două armături. Pentru o creştere constantă a tensiunii, trebuie să existe prin urmare şi o creştere constantă a sarcinii acumulate în condensator, ceea ce se treduce de fapt printr-o deplasare constantă a electronilor între armături, adică existenţa curentului. În această situaţie, condensatorul se comportă precum o sarcină; electronii intră pe armătura negativă şi ies din armătura pozitivă, acumulând energie sub formă de câmp electric.

Dacă repetăm scenariul de mai sus, doar că în acest caz, mărim rata de deplasare a periei condensatorului, variaţia tensiuni (dv/dt) va avea o valoare mai mare; curentul prin condensator va fi şi el mai mare în acest caz:

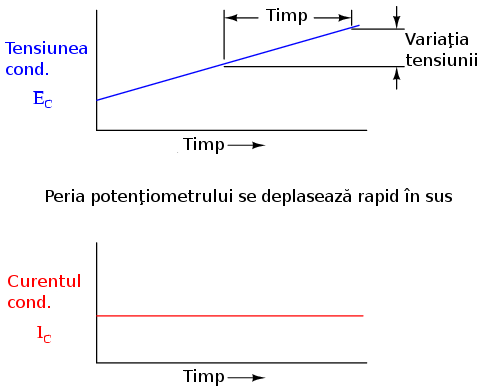
Analiza matematica introduce de fapt conceptul de rată de variaţie pentru o varietate de funcţii. Derivata unei funcţii, un principiu de bază al analizei matematice, este expresia variaţiei unei variabile în funcţie de o altă, în cazul nostru, variaţia tensiunii în funcţie de timp. Mai simplu spus, curentul printr-un condensator este direct proportional cu viteza de variaţie a tensiunii la bornele acestuia.

Să luăm acum un alt exemplu. Dacă de data aceasta deplasăm peria potenţiometrului în aceeiaşi direcţie ca şi inainte („sus”) dar nu constant ci la viteze (rate de variaţie) diferite. În acest caz obţinem un grafic al variaţiei tensiunii şi curentului ce arată aproximativ asfel:

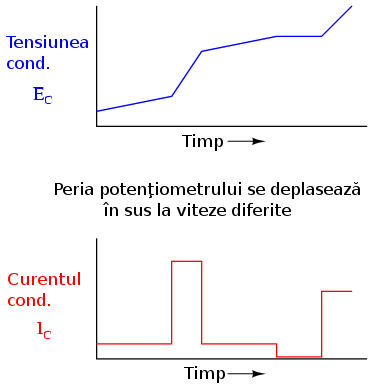
Putem observă de pe grafic că tot timpul curentul prin condensator este proporţional cu rata de variaţie sau panta tensiunii condensatorului. Când graficul tensiunii creşte rapid (pantă mare), curentul este de asemenea mare. Când panta tensiunii este mai mică, şi curentul este mai mic. La un moment dat panta tensiunii este zero (linie orizontală), datorită faptului că peria potenţiometrului nu s-a deplasat deloc în acest interval de timp; în acest caz, curentul prin condensator este zero (vezi graficul).

Dacă deplasăm în schimb peria potenţiometrului în „jos”, tensiunea la bornele condensatorului va scădea. Din nou, condensatorul reacţionează la această variaţie de tensiune prin producerea unui curent în sensul contrar de această dată. O descreştere a tensiunii unui condensator presupune că diferenţa de sarcină dintre armăturile condensatorului se reduce, singurul mod în care acest lucru se poate întâmpla este dacă electronii îşi schimbă direcţia de deplasare; condensatorul în acest caz se descarcă. În aceast caz, în care electronii ies de pe armătura negativă şi intră pe cea pozitivă, condensatorul se comportă precum o sursă (ex, o baterie), eliberând în circuitul extern energia stoacată sub formă de câmp electric.

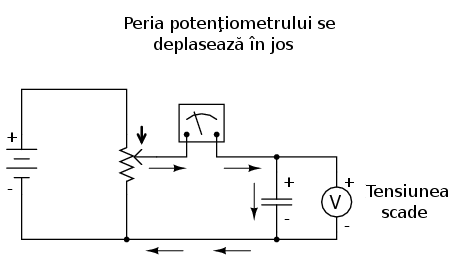
Din nou, cantitatea de curent prin condensator este direct proporţională cu rata de variaţie a tensiunii la bornele sale. Singura difrentă între scăderea şi creşterea tensiunii este direcţia de deplasare a electronilor (direcţia curentului). Pentru o aceeiaşi rată de variaţie a tensiunii cu tipul, valoarea absolută (sau amplitudinea) curentului este exact aceeiaşi. Matematic, o descreştere a tensiunii se traduce printr-o valoarea negativă a raportului dv/dt. Acest lucru se traduce printr-un curent cu semn negativ, indicând de fapt direcţia de deplasare a electronilor la descărcarea condensatorului, în sens opus faţă de încărcarea acestuia.

13.3 Factori ce afectează capacitatea electrică

Există trei factori de bază în construcţia condensatoarelor ce afectează valoarea capacităţii asfel create. Toţi aceşti factori afectează valoarea fluxului de câmp (diferenţa relativă de electroni între armături) dezvoltat între armături pentru o anumită valoare a forţei câmpului electric.

Aria armăturilor

Toţi ceilalţi factori fiind egali, o aria mai mare a armăturilor se traduce printr-o capacitate mai mare a condensatorului; o arie mai mică înseamnă o valoare mai mică a capacităţii. Exmplicaţia constă în faptul că o aria mai mare poate susţine o flux mai mare al câmpului (sarcină colectată pe armături) pentru o anumită valoare a forţei câmpului (tensiunea dintre armături).

Distanţa dintre armături

Toţi ceialţi factori fiind egali, o distanţă mai mare între armături se traduce printr-o capacitate mai mică a condensatorului; o distanţă mai mică între armături înseamnă o capacitate mai mare. Explicaţia constă în faptul că o distanţă mai mică duce la o forţă mai mare a câmpului (tensiunea dintre armături împărţită la distanţa dintre ele), ce rezultă într-un flux mai mare al câmpului (sarcină colectată pe armături), oricare ar fi valoarea tensiunii aplicate pe armături.

Materialul dielectric

Toţi ceilalţi factori fiind egali, o permitivitate mai mare a materialului dielectric se traduce printr-o capacitate mai mare a condensatorului; o valoarea mai mică a permitivităţii înseamnă o capacitate mai mică. Deşi explicaţia este puţin mai complicată, unele materiale oferă o opoziţie mai mică fluxului pentru o anumită valoare a forţei câmpului electric. Materialele cu o permitivitate mai ridicată permit existenţa unui flux mai mare (oferă mai puţină opoziţie), şi prin urmare sarcina colectată pe armături poate fi mai mare, oricare ar fi valoarea forţei câmpului (tensiunea aplicată la bornele condensatorului).

În acest context, „relativ” se referă la permitivitatea materialului relativ la permitivitatea vidului. Cu cât numărul este mai mare, cu atât este mai mare permitivitatea materialului. Sticla, de exemplu, cu permitivitatea relativă 7, are de şapte ori permitivitatea vidului şi va permite prin urmare stabilirea unul câmp electric (flux) de şapte ori mai puternic decâţ este posibil în vid, toţi ceilalţi factori fiind egali.

În următorul tabel sunt prezentate permitivităţile relative (cunoscută şi sub numele de „constanta dielectrică”) ale unor materiale obişnuite:

Material        Permitivitatea relativă (constanta dielectrică)
============================================================ 
Vid ---------------------------- 1.0000                      
Aer ---------------------------- 1.0006                      
PTFE, FEP ("Teflon") ----------- 2.0                         
Polipropilenă ------------------ 2.20 - 2.28                
Răşini ABS --------------------- 2.4 - 3.2                  
Polistiren --------------------- 2.45 to 4.0                
Hârtie ceruită ----------------- 2.5                         
Ulei de transformator ---------- 2.5 - 4                    
Cauciuc tare ------------------- 2.5 - 4.80                 
Lemn (stejar) ------------------ 3.3                         
Silicon ------------------------ 3.4 - 4.3                  
Bachelită ---------------------- 3.5 - 6.0                  
Cuarţ -------------------------- 3.8                         
Lemn (Arţar) ------------------- 4.4                         
Sticlă ------------------------- 4.9 - 7.5                  
Ulei de castor ----------------- 5.0                         
Lemn (Mesteacăn) --------------- 5.2                         
Mică, Muscovit  ---------------- 5.0 - 8.7                  
Mică, Sticlă ------------------- 6.3 - 9.3                  
Porţelan, Steatit -------------- 6.5                         
Alumina ------------------------ 8.0 - 10.0                 
Apă distilată ------------------ 80.0                       
Titanat-Bariu-Stronţiu --------- 7500                      
            

O valoare aproximativă pentru capacitatea unui condensator poate fi calculată cu următoarea formulă:

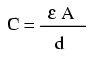
Condensatorul variabil

După modul de construire al condensatorului acesta poate fi fix (discutat mai sus), sau poate fi variabil. Cel mai uşor factor de exploatat în cazul celor variabile este aria armăturilor, sau mai bine spus, aria de suprapunere a lor.

Pe măsură ce rotim axul, gradul de suprapunere al armăturilor variază, afectând aria efectivă în care poate exista campul electric între cele două armături.

13.4 Conectarea condensatorilor în serie şi paralel

Conectarea în serie

La conectarea condensatorilor în serie, capacitatea totală este mai mică decât capcitatea oricărui condensator individual. Dacă doi sau mai mulţi condensatori sunt conectaţi în serie, efectul rezultat este cel al unui condensator (echivalent) avât distanţa dintre armături egală cu suma distanţei dintre armături ale tuturor condensatorilor individuali. După cum am văzut în secţiunea precedentă, creşterea distanţei dintre armături, toţi ceilalţi factorii find egali, rezultă în scăderea capacităţii.

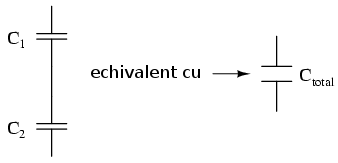
Formula pentru calculul capacităţii serie totale este asemănătoare celei pentru calcularea rezistenţei echivalente la conectarea rezistorilor în paralel.

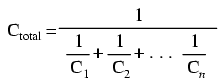
Conectarea în paralel

Atunci când conectarea condensatorilor se realizează în paralel, capacitatea echivalentă totală este suma capacităţilor individuale ale condensatorilor. Dacă doi sau mai mulţi condensatori sunt conectaţi în paralel, efectul rezultat este cel al unui singur condensator (echivalent) având aria armăturilor egală cu suma ariilor armăturilor tuturor condesatorilor. După cum am văzut în secţiunea precedentă, creşterea ariei armăturilor, toţi ceilalţi factori rămânând neschimbaţi, duce la o creştere a capacităţii.

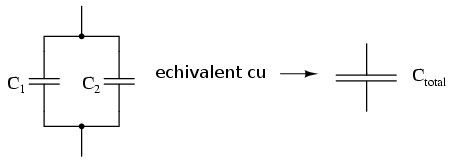
Formula pentru calculul capacităţii paralel totale este asemănătoare celei pentru calcularea rezistenţei echivalente la conectarea rezistorilor în serie:

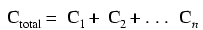
13.5 Consideraţii practice (condensatorul)

Condensatoarele, la fel ca toate celelalte componente, au unele limite de funcţionare şi utilizare. Acestea trebuie respectate dacă dorim o funcţionare corectă şi sigură a circuitelor electrice cu condensatoare.

13.5.1 Tensiunea maximă, polaritate şi condensatorul electrolitic

Din moment ce condensatoarele nu sunt altceva decât doi conductori separaţi printr-un mediu dielectric, trebuie să fim atenţi la tensiunea maximă adimisă la bornele acestora. Dacă aplicăm o tensiune mult prea mare, putem depăşi tensiunea de străpungere a dielectricului, rezultând un condensator scurt-circuitat intern.

Unele condensatoare sunt construite astfel încât să suporte aplicarea unei tensiuni de o anumită polaritate. Acest lucru se datorează modului lor de realizare: dielectricul reprezintă un strat microscopic de material izolator depus pe una dintre armături prin intermediul unei tensiuni de curent continuu. Aceste condensatoare sunt cunoscute sub numele de condensatoare electrolitice, iar polaritatea lor este tot timpul precizată. Simbolul condensatorului electrolitic este prezentat în următoarea figură:

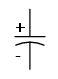
Armătura curbată reprezintă tot timpul armătura negativa. Inversarea polarităţii unui condensator electrolitic duce la distrugerea acelui strat foarte subţire de dielectric şi prin urmare şi a dispozitivului. Totuşi, mărimea dielectricului permite valori mari ale capacităţii relativ la mărimea propriu-zisă a condensatorului. Din acelaşi motiv, condensatoarele electrolitice suportă tensiuni mici faţă de celelalte modele de condensatoare.

13.5.2 Circuitul echivalent al condensatorului

Din moment ce armăturile unui condensator prezintă o anumită rezistenţă electrică, şi, din moment ce niciun dielectric nu este un izolator perfect, este imposibilă crearea unui condensator „perfect”. În realitate, un condensator are atât o rezistenţă serie cât si o rezistenţa paralel (de scurgere) suprapuse peste caracteristicile sale pur capacitive:

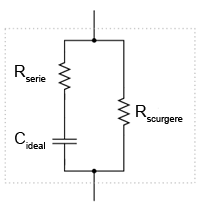
Din fericirea, realizarea condensatoarelor cu o rezisteţă serie foarte mică şi rezistenţă de scurgere foarte mare, este relativ uşoară.

13.5.3 Mărimea fizică a condensatoarelor

În majoritatea aplicaţiilor, mărimea (cât mai mică) joacă un rol ingineresc important. Cu cât componentele sunt mai mici, cu atât mai multe elemente pot fi introduse în circuit, iar greutatea întregului ansamblu scade şi ea.

În cazul condensatoarelor, există doi factori importanţi ce afectează mărimea unui component: tensiunea de lucru şi capacitatea. Aceşti doi factori tind să fie în opoziţie unul cu celălalt. Pentru un anumit dielectric ales, singura modalitate de a creşte tensiunea de lucru a unui condensator este creşterea grosimii dielectricului. Totuşi, după cum am văzut, această situaţie duce la descreşterea capacitătii dispozitivului. Putem readuce capacitatea la valoarea iniţială prin creşterea ariei armăturilor. Dar acest lucru duce la creşterea mărimii fizice a condensatorului. Acesta este motivul pentru care nu putem aprecia capacitatea unui condensator (în Farad) prin simpla observare a mărimii acestuia. Un condensator de o anumită marime, poate avea o capacitate mare şi o tensiune de lucru mică, sau o capacitate mică şi o tensiune de lucru mare, sau un compromis între cele două situaţii. p>