< Curent continuu
16 Constante de timp
16.1 Răspunsul tranzitoriu al condensatorului
Condensatorii tind să se comporte asemenea bateriilor secundare datorită posibilităţii de stocare şi eliberare ulterioară a energiei sub formă de câmp electric. Un condensator complet descărcat generează o tensiune de zero volţi la bornele sale, iar un condensator încărcat menţine o valoare constantă a tensiunii la bornele sale, asemenea unei baterii. Atunci când aceştia sunt introduşi într-un circuit cu alte surse de tensiune, abosrb energie de la aceste surse, la fel precum o baterie secundară se încarcă atunci când este conectată la un generator. Un condensator complet descărcat, având cădere de tensiune zero la bornele sale, conectată la o sursă de tensiune, se va comporta iniţial precum un scurt circuit, „trăgând” un curent maxim de la sursă pe măsură ce se încarcă. Cu timpul, tensiunea la bornele sale creşte spre valoarea tensinii aplicate de sursă, iar curent prin condensator scade din această cauză. După ce condensatorul a atins valoarea maximă a tensiunii sursei, încetează să mai tragă curent de la această, şi se comportă practic precum un circuit deschis.
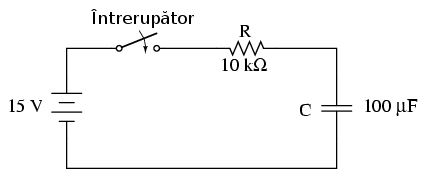
Atunci când întrerupător este închis prima dată, tensiunea la bornele condensatorului (considerat complet descărcat) este de zero volţi; de aceea, în primă fază se comportă precum un scurt-circuit. Cu timpul, tensiunea condensatorului creşte până la valoarea tensiunii bateriei, moment în care condensatorul se comportă precum un circuit deschis. În această configuraţie, curentul prin circuit este determinat de diferenţe de tensiune dintre baterie şi condensator, împărţită la valoarea rezistenţei, 10 kΩ. Pe măsură ce tensiune condensatorului se apropie de cea a baterie, curentul prin circuit se apropie şi el de valoarea zero. Odată atinsă tensiunea bateriei de către condensator (15 V), curentul va fi exact zero.
 **
**
------------------------------------------------ | Timp | Tensiune | Tensiune | Curent | |(secunde) | baterie | condensator | | |----------------------------------------------| | 0 | 15 V | 0 V | 1500 uA | |----------------------------------------------| | 0.5 | 15 V | 5.902 V | 909.8 uA | |----------------------------------------------| | 1 | 15 V | 9.482 V | 551.8 uA | |----------------------------------------------| | 2 | 15 V | 12.970 V | 203.0 uA | |----------------------------------------------| | 3 | 15 V | 14.253 V | 74.68 uA | |----------------------------------------------| | 4 | 15 V | 14.725 V | 27.47 uA | |----------------------------------------------| | 5 | 15 V | 14.899 V | 10.11 uA | |----------------------------------------------| | 6 | 15 V | 14.963 V | 3.718 uA | |----------------------------------------------| | 10 | 15 V | 14.999 V | 0.068 uA | ------------------------------------------------
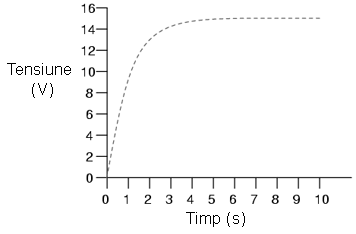
În timp, tensiunea condensatorului se apropie de 15 volţi iar curentul se apropie de zero; acest grafic se numeşte asimptotic, adică, ambele variabile se apropie din ce în ce mai tare de valoarea lor finală cu timpul, dar niciuna nu atinge exact acea valoare. Din punct de vedere practic însă, putem presupune că valoarea tensiunii la bornele condensatorului atinge la un moment dat 15 volţi, iar curentul zero amperi.
16.2 Răspunsul tranzitoriu al bobinei
O bobină complet descărcată (nu există câno magnetic), prin care nu trece niciun curent, la conectarea unei surse de tensiune la bornele sale, se va comporta iniţial asemenea unui circuit deschis (încearcă să menţină un curent de zero amperi), căderea de tensiunea la bornele sale fiind maximă. În timp, curentul creşte spre valoarea maximă permisă de circuit, iar tensiunea scade spre zero. Odată atinsă valoarea de zero volţi (pentru o bobină ideală), curentul rămâne la nivelul maxim, iar bobina se va comporta asemenea unui scurt circuit.
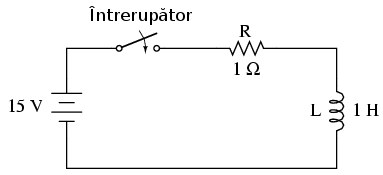
La închiderea întrerupătorului, căderea de tensiune pe bobină sare direct la valoarea tensiunii bateriei (precum un circuit deschis) şi scade spre zero cu timpul (ajungând să se comporte precum un scurt-circuit). Tensiunea pe bobină se determină calculând care este căderea de tensiune de pe R cunoscând curentul prin bobină; diferenţa dintre tensiunea bateriei şi cea a rezistorului este tensiunea de pe bobină. La închiderea iniţială a întrerupătorului, curentul este zero, dar creşte apoi cu timpul până ajunge să fie egală cu raportul dintre tensiunea furnizată de baterie şi rezistenţa rezistorului conectat în serie (1 Ω în acest caz). Comportamentul acest este exact invers faţă de circuitul RC (rezistor-condensator), unde curentul iniţial a fost maxim iar tensiunea pe condensator zero.
 **
**
--------------------------------------------- | Timp | Tensiune | Tensiune | Curent | |(secunde) | baterie | bobină | | |--------------------------------------------| | 0 | 15 V | 15 V | 0 | |--------------------------------------------| | 0.5 | 15 V | 9.098 V | 5.902 A | |--------------------------------------------| | 1 | 15 V | 5.518 V | 9.482 A | |--------------------------------------------| | 2 | 15 V | 2.030 V | 12.97 A | |--------------------------------------------| | 3 | 15 V | 0.747 V | 14.25 A | |--------------------------------------------| | 4 | 15 V | 0.275 V | 14.73 A | |--------------------------------------------| | 5 | 15 V | 0.101 V | 14.90 A | |--------------------------------------------| | 6 | 15 V | 37.181 mV | 14.96 A | |--------------------------------------------| | 10 | 15 V | 0.681 mV | 14.99 A | ---------------------------------------------
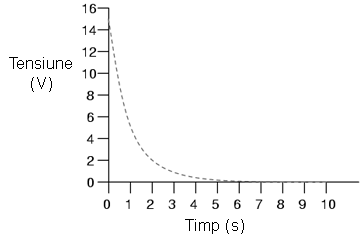
La fel ca în cazul circuitului RC, graficul tensiunii şi al curentului cu timpul este asimptotic.
16.3 Calcularea tensiunii şi a curentului
Valorile iniţiale şi cele finale
Există o metodă sigură de calcul a tuturor variabilelor dintr-un circuit reactiv (cu bobine şi/sau condensatori) de curent continuu. Primul pas este identificarea valorilor iniţiale şi a celor finale pentru tensiune în cazul condensatoarelor şi pentru curent în cazul bobinelor. La închiderea întrerupătorului (sau deschiderea) dintr-un circuit, componentul reactiv încearcă să menţină această cantitate (tensiune pentru condensator, curent pentru bobină) la valoarea existenţă înainte de acţionarea întrerupătorului; această valoarea este prin urmare folosită ca valoare „iniţială”. Valoarea finală a acestei mărimi este cantiatea la care ajunge după o durată de timp infinită de la acţionarea întrerupătorului. Aceasta poate fi determinată în analiza circuitului capacitiv considerând condensatorul un circuit deschis, iar în cazul analizei circuitului inductiv, condiderând bobina un scurt-circuit, deoarece acesta este comportamentul lor după ce sunt încărcate la maxim (dupa o perioadă de timp infinită).
Constanta de timp
Următorul pas este calcularea constantei de timp a circuitului: timpul necesar pentru ca valorile tensiunii şi ale curentului să variaze cu aproximativ 63% de la valorile lor de pornire până la valorile finale, într-o situaţie tranzitorie. Într-un circuit RC serie, constanta de timp este egală cu produsul dintre rezistenţa totală în ohmi şi capacitatea în farazi. Pentru un circuit serie L/R, constanta de timp este egală cu raportul dintre inductanţa totală în Henry şi rezistenţa totală în ohmi. În ambele cazuri, constanta de timp se exprimă în secunde şi este simbolizată prin litera grecească „tau”, τ:
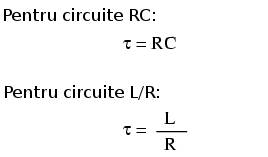
Creşterea şi descreşterea valorilor circuitului reactiv tranzitoriu, este asimptotică, curbele graficului sunt prin urmare exponenţiale.
După cum am spus mai sus, constanta de timp este durata de timp necesară pentru ca oricare dintre aceste valori să varieze cu 63% faţă de valoarea lor iniţială spre cea finală. Cu fiecare constantă de timp, aceste valori se situează cu 63% mai aproape de valoarea lor finală. Formula matematică pentru determinarea precisă a procentelor variaţiei este următoarea:
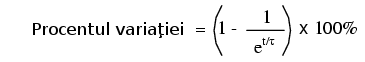
Litera e este constanta lui Euler, aproximativ 2.7182818. La formula de mai sus s-a ajuns cu ajutorul analizei matematice, după analiza asimptotică a valorilor circuitului. După un timp egal cu o constantă de timp, procentul variaţiei faţă de valoarea iniţială este de:
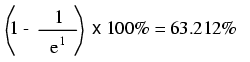
După o perioadă de două constante de timp, procentul variaţiei faţă de valoarea iniţială este:
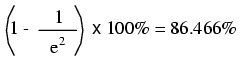
După zece constante de timp:
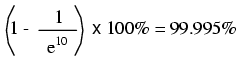
Cu cât perioada de timp de la aplicarea tensiunii bateriei la bornele bobinei/condensatorului este mai lungă, cu atât este mai mare valoarea numitorului fracţiei, întraga fracţie fiind asfel mai mică, iar totalul scăzut din valoarea 1 se apropie eventual spre 1, sau, 100%.
Putem deduce o formulă universală pentru determinarea valorile curentului şi ale tensiunii în circuitele tranzitorii, prin înmulţirea aceste valori cu diferenţa dintre valorile iniţiale şi cele finale ale tensiunii/curentului:

Analiza circuitului RC
Să analizăm circuitul RC serie de la începutul capitolului:

Din moment ce constanta de timp (τ) a unui circuit RC serie este produsul dintre rezistenţă şi capacitate, valoarea obţinută este de 1 secundă:
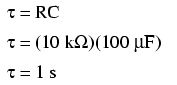
Analiza tensiunii
Analizăm în acest caz tensiunea deoarece este valoarea pe care condensatoarele încearcă să o menţină constantă. Cu toate că formula se poate aplica la fel de bine şi pentru curent, valorile finale şi cele iniţiale petru curent sunt de fapt derivate din tensiunea condensatorului, prin urmare, calcularea tensiunii este o metodă mai directă. Rezistenţa este de 10 kΩ iar capacitatea de 100 µF (microfarad).
Dacă iniţial condensatorul este complet descărcat (0 V), putem folosi această valoare pentru tensiunea iniţială. Valoarea finală va fi tensiunea bateriei, 15 V. Formula universală pentru tensiunea condensatorului în acest circuit arată asfel:
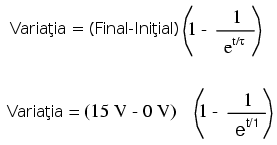
După 7.25 de secunde de la aplicarea tensiunii la bornele condensatorului (prin închiderea întrerupătorului), tensiunea va creşte asfel:
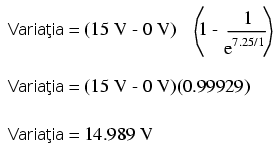
Deoarece tensiunea iniţială la bornele condensatorului a fost de 0 V, o creştere cu 14.989 V se traduce printr-o cădere de tensiune de 14.989 la bornele condensatorului după 7.25 s de la inchiderea circuitului.
Analiza curentului
Aceeiaşi formulă poate fi folosită şi pentru determinarea curentului din circuit. Ştim că un condensator descărcat se comportă precum un scurt circuit, prin urmare, curentul iniţial va fi maximul posibil în circuit:
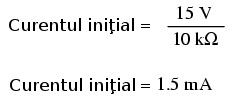
Ştim de asemenea că valoarea finală a curentului va fi zero, din moment ce condensatorul se va comporta eventual precum un circuit deschis, prin uramre, nu va exista curgere a electronilor prin circuit. Cunoscând valorile iniţiale şi cele finale, putem folosi formula universală pentru determinarea valorii curentului după 7.25 de secunde de la închiderea aceluiaşi circuit RC de mai sus:

Observăm că valoarea obiţinută este negativă, nu pozitivă! Acest lucru înseamă o descreştere a curentului şi nu creştere a acestuia în timp. Din moment ce am început cu un curent de 1.5 mA, această descreştere de 1.4989 mA se traduce prin existenţa unui curent de 0.001065 mA (1.065 µA) după un interval de timp de 7.25 de secunde de la închiderea circuitului.
Am fi putut determina curentul prin circuit după 7.25 s, scăzând tensiunea condensatorului din tensiunea bateriei pentru obţinerea tensiunii pe rezistor; aflam apoi curentul prin rezistor (şi prin întreg circuitul) folosing legea lui Ohm (I=E/R). În ambele cazuri, ar trebui să obţinem acelaşi răspuns:
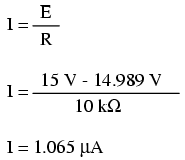
Analiza circuitului L/R
Să analizăm acum circuitul L/R serie de la începutul capitolului:

Cu o inductanţă de 1 Henry şi o rezistenţă serie de 1 ohm, constanta de timp a circuitului de faţă este de 1 secundă:
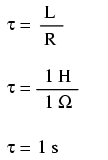
Analiza curentului
Deoarece este un circuit inductiv, iar bobinele ştim că se opun variaţiei curentului, vom aplica formula universală folosind valorile iniţiale şi finale ale curentului. Dacă îniţial întrerupătorul este deschis, curentul este egal cu zero (valoarea iniţială). După o perioadă de timp infinită, curentul va atinge valoarea sa finală, egală cu raportul dintre tensiunea sursei şi rezistenţa totală din circuit (I=E/R), 15 A în acest caz.
Dacă vrem să aflăm valoarea curentului la 3.5 secunde după închiderea întrerupătorului, aplicăm formula universală asfel:
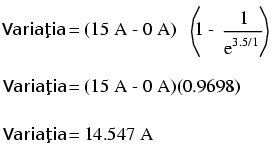
Din moment ce valoarea iniţială a curentului a fost zero, valoare acestuia după 3.5 secunde este de 14.547 amperi.
Analiza tensiunii
Având doar un singur rezistor în circuit, calculăm mai întâi căderea de tensiune pe acesta pentru timpul de 3.5 s:

Făcând diferenţa între tensiunea bateriei şi cea a rezistorului, căderea de tensiune pe bobină este de 0.453 pentru timpul de 3.5 s

16.4 De ce L/R şi nu LR
Pentru cei care studiază teoria circuitelor electrice pentru prima dată, este destul de greu de înţeles motivul pentru care calculul constantei de timp pentru un circuit inductiv este diferit faţă de circuitul capacitiv. Pentru un circuit rezistor-condensator (RC), constanta de timp (în secunde) se calculează ca produs dintre rezistenţă în ohmi şi capacitatea în Farad: τ=RC. Totuşi, pentru un circuit rezistor-bobină (L/R), constanta de timp se calculează ca raport dintre inductanţa în Henry şi rezistenţă în ohmi: τ=L/R.
Această diferenţă a modului de calcul are implicaţii profunde asupra analizei calitative a răspunsului tranzitoriu al circuitului. Circuitele RC au un răspuns mai rapid pentru o valoare mică a rezistenţei şi un răspuns mai lent pentru o valoare mare a rezistenţei; circuitele L/R sunt exact opusul, răspund mai rapid cu o rezistenţă mai mare şi mai lent pentru una mai mică. Circuitele RC în general sunt destul de intuitive, dar cele inductive sunt mai greu de înţeles.
Cheia care stă la baza înţelegerii circuitelor tranzitorii este o înşuşire temeinică a conceptului transferului de energie şi natura sa electrică. Atât condensatoarele cât şi bobinele pot stoca energie, condensatorul sub formă de câmp electric iar bobina sub formă de câmp magnetic. Energie electrostatică a condensatoruli tinde să menţină constantă valoarea tensiunii de la terminalele sale. Energia electromagnetică a bobinei tinde să menţină constantă valoarea curentului prin ea.
Descărcarea condensatorului şi a bobinei pe un rezistor
Să luăm în considerare ce se întâmplă în cazul fiecărui component reactiv în momentul descărcării, şi anume, atunci când energia stocată în dispozitiv (bobină sau condensator) este eliberată pe un rezistor şi disipată de acesta sub formă de căldură:
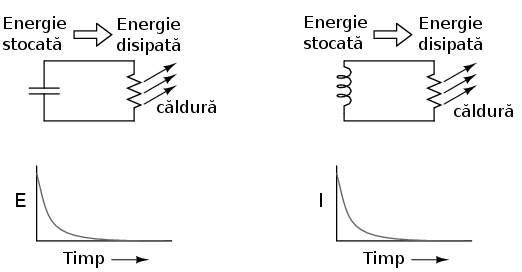
În ambele cazuri, căldura disipată pe/de rezistor constituie energie ce părăseşte circuitul, în consecinţă, componentul reactiv (condensatorul sau bobina) îşi pierde energia stocată în timp; rezultatul este fie o descreştere a tensiunii condensatorului sau o descreştere a curentului bobinei, lucru reprezentat pe grafic. Cu cât rezistorul disipă mai multă putere, cu atât mai rapidă este descărcarea dispozitivelor, deoarece puterea, prin definiţie, este rata transferului de energie cu timpul.
Prin urmare, constanta de timp a unui circuit tranzitoriu depinde de rezistenţa circuitului. Desigur, aceasta depinde şi de capacitatea de stocare a componentului reactiv, dar ne vom concentra momentan doar pe efectul rezistorului asupra circuitului. Constanta de timp a circuitului este mai mică (o rată de descărcare mai rapidă) dacă valoarea rezistorului este în aşa fel încât maximizează disiparea puterii (rata transformării energiei în căldură) din circuit. Pentru un circuit capacitiv, unde energia stocată este sub formă de tensiune, acest lucru înseamnă că rezistorul trebuie să aibe o valoare mică a rezistenţei pentru maximizarea curentului, oricare ar fi tensiunea existenţă. Pentru un circuit inductiv, unde energia stocată este sub formă de curent, acest lucru înseamnă că rezistorul trebuie să aibă o valoare mare a rezistenţei pentru maximizarea căderii de tensiune, oricare ar fi valoarea curentului (luând în considerare faptul că produsul dintre tensiune şi curent este egal cu puterea).
Analogie mecanică pentru modul de stocare al energiei din componentele reactive
Ca şi o analogie, putem recurge la o exemplificare mecanică a stocării energiei sub formă capacitivă şi inductivă. Condensatoarele, stocând energie electrostatic, sunt rezervoare de energie potenţială. Bobinele, stocând energie electromagnetic (electro/dinamic/), sunt rezervoare de energie cinetică. Mecanic, energia potenţială poate fi reprezentată cu ajutorul unei mase suspendate, iar energia cinetică cu ajutorul unei mase aflate în mişcare.
Analogia mecanică a energiei potenţiale pentru condensator
Să considerăm următoarea ilustraţie pentru condensator, considerând energia stocată în acest ca fiind energie potenţială:
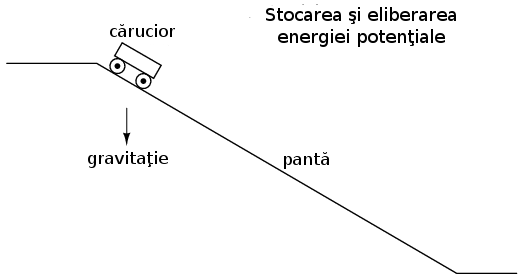
Căruciorul, atunci când se afla în vârful pantei, posedă energie potenţială datorată influenţei gravitaţiei şi poziţiei sale din vârf. Dacă luăm în considerare sistemul de frânare al căruciorului, acesta este analog rezistenţei circuitului/sistemului, iar căruciorul este în acest caz condensatorul; întrebarea este, ce valoare (mică sau mare) a rezistenţai ajută la o eliberare mai rapidă (parcurgerea mai rapidă a pantei) a energiei potenţiale? Desigur, o rezistenţă minimă (lipsa frânelor) ar duce la parcurgerea cea mai rapidă a pantei de către cărucior! Fară ca sistemul de frânare să acţioneze, căruciorul se va deplasa liber pe pantă în jos, folosind („consumând”) energie potenţială pe măsură ce pierde din înălţime. Atunci când sistemul de frânare acţionează la capacitate maximă, căruciorul nu se va deplasa la vale (sau o va face foarte încet), iar energia sa potenţială se va păstra pentru o perioadă mai îndelungată de timp. Acelaşi lucru se întâmplă şi în cazul circutului capacitiv, ce se descarcă rapid dacă rezistenţa sa este mică, şi se descarcă lent dacă rezistenţa este mare.
Analogia mecanică a energiei cinetice pentru bobină
Să considerăm acum o analigie mecanică pentru bobină, reprezentând energie stocată de acesta sub formă cinetică:

De această dată, căruciorul se află la nivelul solului şi este deja în mişcare. Energia sa în acest caz este energie cinetică (mişcare), nu potenţială (înălţime). Din nou, considerând sistemul de frânare al căruciorului ca fiind analog rezistenţei din circuit, atunci putem considera căruciorul ca fiind bobina; întrebarea în acest caz este este asemănătoare celei din cazul condensatorului, şi anume, ce valoare a rezistenţei facilitează eliberarea rapidă a energiei cinetice stocate? Desigur, o rezistenţă maximă (sistemul de frânarea acţionat la maxim) va încetini căruciorul cel mai repede (într-o perioadă de timp cât mai scurta). Cu sistemul de frânare acţionat la maxim, căruciorul se va opri foarte repede, folosind („consumând”) energia cinetică pe măsură ce încetineşte. Fără acţiunea frânelor, căruciorul se deplasează liber, pentru o perioadă de timp infinita (neglijând frecarea şi rezistenţa aerodinamică în acest caz, de dragul exemplificării), iar energia sa cinetică va fi menţinută (stocată) pentru o perioadă lungă de timp. Analog, un circuit inductiv se descarcă rapid dacă rezistenţa pe care se descarcă este mare şi invers, se descarcă lent dacă rezistenţa este mică.
16.5 Cazuri speciale de calcul
Există cazuri de analiză a circuitelor de curent continuu tranzitorii în care componentele reactive (condensatori sau bobine) nu sunt iniţial „descărcate”, prin urmare, valorile iniţiale ale tensiunii şi curentului nu sunt zero. Cu alte cuvinte, condensatorul poate fi parţial încărcat la momentul iniţial (tensiunea la bornele sale este diferită de zero), iar bobina poate fi deja străbătuta de un anumit curent la momentul iniţial. Să luăm următorul circuit ca şi exemplu; iniţial întrerupătorul este deschis, iar la momentul final acesta este închis:
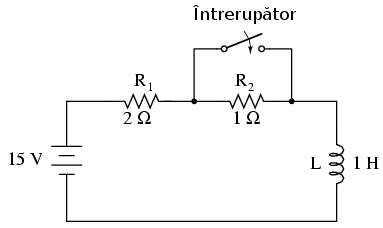
Deoarece acesta este un circuit inductiv, începem analiza prin determinarea valorilor iniţiale şi finale ale curentului. Acest pas este extrem de important în analiza circuitelor inductive, deoarece valorile iniţiale şi finale ale tensiunii nu pot fi cunoscute decât după determinarea curentului! Cu întrerupătorul în poziţia deschis (condiţia iniţială), rezistenţa serie totală este de 3 Ω, ceea ce limitează valoarea finală a curentului din circuit la 5 A:
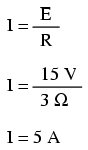
Asfel, chiar înainte de a închide întrerupătorul, avem un curent de 5 A prin bobină, faţă de 0 A în exemplul din secţiunea precedentă (link!). Când întrerupătorul este închis (condiţia finală), rezistorul de 1 Ω este scurt-circuitat, iar valoarea totală a rezistenţei din circuit se reduce la 2 Ω (R1); valoarea finală a curentului prin circuit cu întrerupătorul închis este:
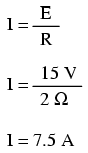
Prin urmare, bobina din acest circuit are un curent iniţial de 5 A şi unul final de 7.5 A. Deoarece ne interesează ce se întâmplă în circuit după închiderea întrerupătorului şi scurt-circuitarea rezistorului R2, calcularea constantei de timp se calculează pentru L1 şi R1: 1 Henry / 2 Ω, sau τ = 1/2 secunde. Cu aceste valori, putem acum calcula valorile curentului în timp. Tensiune pe bobină este egală cu diferenţa dintre tensiunea bateriei (15 V) şi produsul dintre curentul circuitului (7.5 A) şi rezistenţa R1 (2 Ω). Dacă observăm că tensiunea iniţială la bornele bobinei este de 5 V şi apoi scade la 0 volţi după un timp infinit de la închiderea întrerupătorului, putem folosi aceste valori în formula universală a constantei (link!) de timp pentru a ajunge la aceleaşi rezultate:
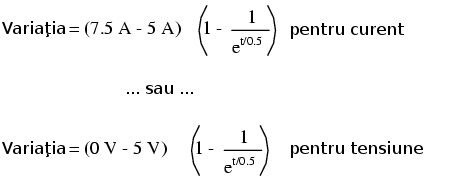
|-------------------------------------------| | Timp | Tensiune | Tensiune | Curent | |(secunde) | baterie | bobină | | |-------------------------------------------| | 0 | 15 V | 5 V | 5 A | |-------------------------------------------| | 0.1 | 15 V | 4.094 V | 5.453 A | |-------------------------------------------| | 0.25 | 15 V | 3.033 V | 5.984 A | |-------------------------------------------| | 0.5 | 15 V | 1.839 V | 6.580 A | |-------------------------------------------| | 1 | 15 V | 0.677 V | 7.162 A | |-------------------------------------------| | 2 | 15 V | 0.092 V | 7.454 A | |-------------------------------------------| | 3 | 15 V | 0.012 V | 7.494 A | |-------------------------------------------|
16.6 Circuite complexe
Ce facem în cazul în care avem un circuit mai complicat decât configuraţiile serie considerate până acum? Să luăm acest circuit, de exemplu:
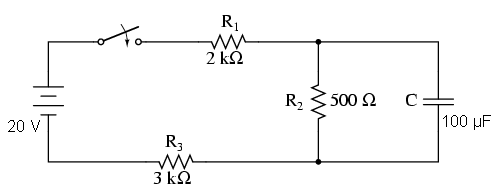
Formula constantei de timp (τ=RC) se bazează pe un circuit capacitiv serie simplu, format dintr-un condensator şi un rezistor conectate în serie. Acelaşi lucru este valabil şi pentru constanta de timp în circuitul inductiv serie simplu (τ=L/R). Ce putem face prin urmare într-o situaţie asemănătoare celei de faţă, unde rezistorii sunt conectaţi într-o configuraţie serie-paralel cu condensatorul/bobina?
Răspunsul este că putem folosi metodele învăţate la analiza reţelelor (link!). Teorema lui Thevenin ne spune că putem reduce oricare circuit liniar la un circuit echivalent compus dintr-o sursă de tensiune, un rezistor conenctat în serie cu aceasta şi o sarcină, urmând câţiva paşi simpli. Pentru aplicarea teoremei lui Thevenin la circuitul de faţă, considerăm componentul reactiv, condensatorul, ca fiind sarcina; pasul următor este îndepărtarea acestuia din circuit pentru determinarea tensiunii şi a rezistenţei Thevenin. Apoi, dupa ce am determinat valorile din circuitul echivalent, reconectăm condensatorul şi determinăm tensiunea şi curentul în funcţie de timp, exact cum am făcut şi până acum.
După ce am identificat condensatorul ca fiind „sarcina” circuitului, îl îndepărtăm şi determinam tensiunea la bornele sarcinii (întrerupătorul este închis)
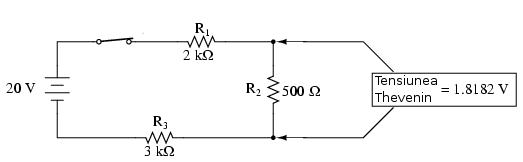
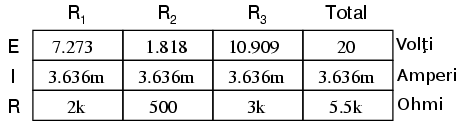
Acest pas al analizei reflectă faptul că tensiunea la bornele sarcinii (aceeiaşi ca la bornele rezistorului R2) este de 1.8182 V atunci când nu este conectată nicio sarcină. Dacă suntem atenţi, observăm că această tensiunea este chiar tensiunea finală la bornele condensatorului, deoarece un condensator complet încărcat se comportă precum un circuit deschis (curent zero). Folosim această valoare a tensiunii pentru circuitul echivalent Thevenin.
Pentru determinarea rezistenţei Thevenin, trebuie să eliminăm toate sursele de putere din circuitul original şi să recalculăm rezistenţa aşa cum este ea văzută de la terminalele sarcinii:
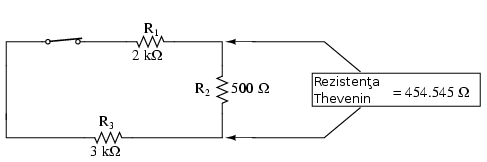
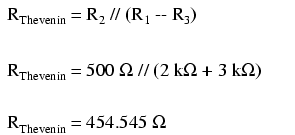
Următorul pas este redesenarea circuitului original sub forma circuitului echivalent Thevenin:
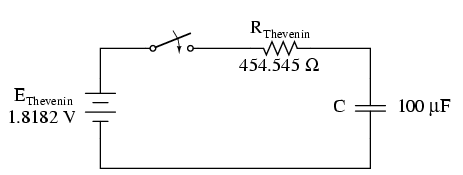
Constanta de timp pentru acest circuit va fi egală cu produsul dintre rezistenţa Thevenin şi capacitatea condensatorului (τ=RC). Cu valorile de mai sus, putem face următoarele calcule:

În acest moment putem afla şi tensiunea la bornele condensatorului direct din formula universală de calcul a constantei de timp. Să facem calculele pentru o valoare de 60 de milisecunde. Deoarece este o formulă capacitivă, vom face calculele în funcţie de tensiune:
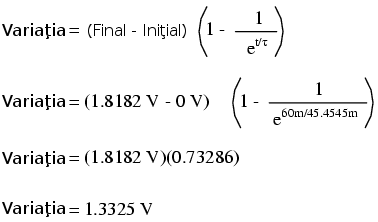
Din nou, deoarece valoarea iniţială a tensiunii condensatorului am presupus-o ca fiind zero volţi, căderea de tensiune actuală pe condensator dupa un interval de 60 ms de la închiderea întrerupătorului este suma dintre valoarea iniţială (0 V) şi cea finală (1.3325 V), adică 1.3325 V.
16.7 Rezolvarea circuitului pentru variabila timp
În unele cazuri este necesară determinarea duratei de timp pentru care circuitul va atinge o valoarea predeterminată. Acest lucru este în special întâlnit în cazurile în care proiectăm circuitul RC sau L/R pentru o aplicaţie în funcţie de timp. Pentru acest calcul, trebuie să modificăm formula universală a constantei de timp. Cea originală arată asfel:
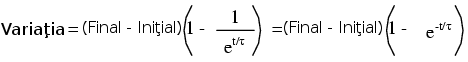
În acest caz dorim însă să realizăm un calcul în funcţie de timp. Pentru aceasta, modificăm formula, şi scoatem variabila timp în stânga formulei, în loc de „variaţie”:
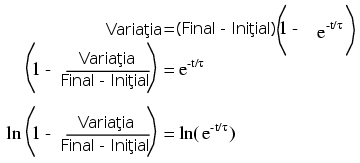
Unde ln reprezintă logaritmul natural: inversa lui e:
Dacă ex = a, atunci ln a = x: puterea la care trebuie ridicat e pentru a produce rezultatul a
Exemplu
Folosim acelasi circuit rezistor-condensator de la începutul capitolului şi ne folosim de datele deja determinate pentru a afla durata de timp pentru a ajunge la ele:

Constanta de timp este aceeiaşi, 1 secundă (10 kΩ înmulţit cu 100 µF); iar valorile iniţiale şi finale rămân şi ele neschimbate (tensiunea iniţială a condensatorului este iniţial 0 V, iar finală 15 V). După cum reiese din tabelul de la începutul capitolului (link!), după 2 secunde condensatorul va fi încărcat la 12.970 V. Să întroducem aşadar valoarea de 12.970 V în formula determinată mai sus pentru a vedea dacă timpul rezultat este de 2 secunde:

Într-adevăr, răspunsul este cel aşteptat, şi anume 2 secunde. Putem însă afla duratele de timp necesare încărcarii condensatorului pentru oricare valoare din intervalul (iniţial, final). De exemplu, care este durata de timp pentru care condensatorul se încarcă la 10 V? p>