< Curent continuu
12 Fizica conductorilor
12.1 Introducere fizica conductorilor
Ar trebui să fiţi deja familiarizaţi cu legătura ce există între conductivitatea electrică şi tipul materialului. Acele materiale ce permit trecerea uşoară a electronilor liberi, poartă numele de conductori, pe când cele ce se opun trecerii electronilor prin ele, poartă numele de materiale dielectrice.
Din păcate, teoriile ştiinţifice ce explică motivul pentru care unele materiale sunt conductoare iar altele nu, sunt destul de complexe, şi conţin explicaţii despre modul de aranjare al electronilor în jurul nucleelor atomilor. Contrar modelului „planetar” atât de răspândit, conform căruia electronii se deplasează în jurul nucleului atomului precum nişte bucăţi de materie sub forma orbitelor eliptice, electronii nu se comportă deloc precum nişte bucăţi de materie. De fapt, electronii posedă atât caracteristici ale particulelor cât şi ale undelor, comportamentul lor fiind determinat de plasarea lor în zona distincte din jurul nucleului, zone denumite straturi sau substraturi. Electronii pot ocupa aceste zone doar într-o anumită bandă de energie, în funcţie de zona respectivă şi de prezenţa altor electroni. Dacă electronii s-ar comporta într-adevăr precum nişte planete ţinute pe orbita nucleului de către atracţia electrostatică, iar comportamentul lor fiind descris în acest caz de aceleaşi legi ce descriu mişcarea planetelor adevărate, atunci nu ar exista nicio distincţie reală între materialele conductoare şi dielectrice, iar legăturile chimice dintre atomi nu ar exista sub forma pe care o cunoaştem în acest moment. Aceste fenomene se datorează prin urmare naturii discrete, cuantificate a energiei electronilor şi poziţionării acestora, aşa cum sunt ele descrise de fizica cuantică.
Atunci când un electron este liber să treacă într-o stare energetică mai mare în jurul nucleului atomului (datorită plasării acestuia într-un anumit strat), acesta este liber să se „desprindă” de atomul său şi să constituie o parte a curentului electric prin substanţa din care face parte atomul respectiv. Acest scenariu este tipic materialelor conductoare. Dacă limitările cuantice impuse unui electric nu-i permit această liberate, se consideră că electronul este „legat” şi nu se poate desprinde de atom (cel puţin, nu uşor) pentru a lua parte la curentul total din substanţă. Acest scenariu este tipic materialelor dielectrice (izolatoare).
12.1.1 Conductivitatea electrică
În unele texte de specialitate este afirmat faptul că atât conductivitatea cât si non-conductivitatea unui element este determinată exclusiv de numărul electronilor din stratul de valenţă (stratul exterior al atomului). Această explicaţie este însă o simplificare exagerată, fapt ce devine aparent în momentul în care consultăm tabelul elementelor şi comparăm conductivitatea materialelor cu numărul electronilor de valenţă (numărul electronilor de pe ultimul strat). Adevărata complexitate a problemei este scoasă la lumină atunci când luăm în considerare conductivitatea moleculelor (mai mulţi atomi legaţi între ei prin intermediul activităţii electronilor).
Un exemplu pertinent în acest sens este carbonul, ce cuprinde două materiale de conductivităţi total diferite: grafitul şi diamantul. Grafitul este un conductor mediu de electricitate, pe când diamantul este practic un dielectric; tehnic însă, diamantul este clasificat ca şi semiconductor - material ce se comportă precum un dielectric în forma sa pură, dar poate conduce la temperaturi înalte sau/şi sub influenţa impurităţilor. Atât grafitul cât şi diamantul sunt compuse din exact aceleaşi tipuri de atomi, şi anume, din atomi de carbon ce conţin 6 protoni, 6 neutroni şi 6 electroni fiecare. Diferenţa fundamentală dintre cele două tipuri de materiale o constituie modul de aranjare al atomilor de carbon pentru formarea structurii.
Dacă atomii de carbon formează compuşi cu alte tipuri de atomi, conductivitatea electrică este din nou afectată. Carbura de siliciu (SiC), un compus al carbonului cu siliciul, prezintă un comportament neliniar: rezistenţa sa electrică descreşte odată cu creşterea tensiunii aplicate (rezistenţă negativă). Compuşii pe bază de hidrocarburi, precum produsele petroliere, sunt în general dielectrici foarte buni.
După cum putem vedea, simpla numărare e electronilor de valenţa a unui atom nu este un indicator foarte bun pentru conductivitatea electrice a materialului în cauză.
Toate elementele metalice sunt buni conductori de electricitate, datorită tipului de legături dintre atomi. Electronii atomilor metalelor sunt liberi să se deplaseze între nivelurile energetice, astfel că aceştia „plutesc” liber între diferitele nuclee din componenţa substanţei, fiind „motivaţi” foarte uşor de prezenţa unui câmp electric. De fapt, electronii sunt într-atât de mobili încât ne putem imagina că nucleele atomilor „plutesc într-o mare de electroni”. Această mobilitate este răspunzătoare şi de alte propritetăţi bine cunoscute ale metalelor: conductivitate termică, maleabilitate şi ductilitate.
Din fericire, fizica din spatele tuturor acestor fenomene este în mare parte irelevantă pentru scopul acestei cărţi, deşi o înţelegere a principiilor fizice ce stau la baza funcţionării circuitelor electrice sau electronice reprezintă un atu extrem de important în orice împrejurare.
Un pas important în „stăpânirea” curentului electric, este construirea căilor conductoare necesare deplasării electronilor şi controlul acestora prin intermediul rezistenţelor. De asemenea, este la fel de importantă prevenirea deplasării electronilor în locuri nedorite, folosind materiale dielectrice. Totuşi, nu toţi conductorii sunt la fel; acelaşi lucru este valabil şi în cazul dielectricilor. Trebuie să înţelegem prin urmare unele caracteristici principale ale conductorilor şi dielectricilor, pentru a le putea aplica în circuitele reale.
Aproape toţi conductorii posedă o anumită rezistenţă măsurabilă (în afară de supraconductoare). În mod normal, presupunem că rezistenţa conductorilor dintr-un circuit este zero, iar curentul ce trece prin ei nu prezintă nicio cădere de tensiune. În realitate, va exista tot timpul o cădere de tensiune în lungul conductorilor, fie că o dorim sau nu.
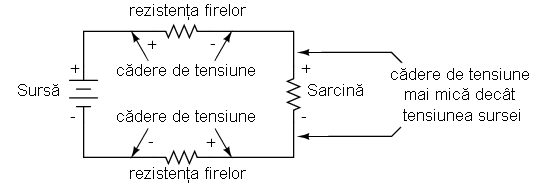
Pentru a putea calcula aceste căderi de tensiuni în oricare circuit, trebuie să putem determina rezistenţa oricăror conductori, cunoscând materialul din care este confecţionat, diametrul precum şi lungimea acestuia, lucru ce-l vom explora în următoarele capitole.
12.2 Mărimea şi amperajul conductorilor
12.2.1 Diametrul conductorilor si deplasarea electronilor
Ar trebui să ne putem da seama de faptul că lichidele ce curg prin conducte cu diametru mare trec mai uşor decât lichidele ce curg prin conducte de diametru mic (ca şi exemplu practic, încercaţi să beţi un lichid folosind paie de diametre diferie). Acelaşi principiu general se aplică şi în cazul deplasării electronilor prin conductori: cu cât secţiunea transversală (grosimea) a conductorului este mai mare, cu atât există mai mult loc pentru deplasarea electronilor; acest lucru se traduce printr-o rezistenţă mai mică.
12.2.2 Tipuri de conductoare
Conductoarele electrice sunt de obicei rotunde, deşi există câteva excepţii de la această regulă, şi confecţionează în două variante de bază: solid şi răsucit. Conductoarele de cupru solide sunt exact asta: un singur fir de cupru pe toată lungimea cablului. Cele răsucite sunt format din mai multe fire solide de cupru răsucite împreună pentru a forma un singur conductor mai mare. Cel mai mare avantaj al cablurilor răsucite constă în flexibilitatea lor mecanică, fiind capabile să suporte îndoituri şi răsuciri repetate mult mai bine decât un singur fir de cupru; acesta din urmă tinde să „îmbătrânească” şi să se deterioreze (rupă) cu timpul.
12.2.3 Mărimea conductorilor - aria secţiunii transversale
Mărimea firelor poate fi măsurată în mai multe moduri. Am putea vorbi despre diametru firului, dar, din moment ce elementul cel mai important legat de deplasarea electronilor este de fapt aria secţiunii transversale, cel mai corect este să desemnăm mărimea unui fir prin intermediul acestei arii.
Figure 470: secţiunea transversală printr-un conductor şi aria acesteia Desigur, secţiunea transversală a firului de sus nu este reprezentată la scară. Diametrul firului este de 1,13 mm. Calculând aria secţiunii transversale cu formula de mai jos, obţinem rezultatul de 1 mm2:A = πr2 A = 3,14 (1,13 / 2)2 A = 1 mm2
12.2.4 Bare metalice conductoare
Pentru anumite aplicaţii ce utilizează curenţi mari, dimensiunea maximă practică a firelor circulare nu este suficientă. În aceste situaţii se folosesc bare metalice pe post de conductori. Acestea sunt realizate în general din cupru sau aluminiu, şi de cele mai multe ori nu sunt izolate. Cea mai întâlnită forma este cea rectangulară, dar nu este singura.
12.2.5 Amperajul conductorilor
Cu cât aria secţiunii transversale a conductorului este mai mică, cu atât este mai mică rezistenţa conductorului pentru a ceeiaşi lungime a sa, toţi ceilalţi factori ramânând constanţi. Un conductor cu o rezistenţă mai mare va disipa o cantitate mai mare de energie sub formă de căldura, oricare ar fi valoarea curentului, puterea fiind egală cu P = I2R.
Puterea disipată într-o rezistenţă se manifestă sub formă de căldură, iar căldura excesivă poate distruge conductorul, cât şi obiectele din jurul acestuia, şi în special materialul izolant din jurul acestuia ce se poate topi şi chiar arde. Conductorii mai subţiri, prin urmare, vor tolera un curent de o valoare mai mică decât conductorii groşi, toţi ceilalţi factori rămânând constanţi. Curentul maxim pe care un conductor îl poate susţine, fără a duce la distrugerea acestuia, poartă numele de amperaj.
Tabelele tipice pentru amperajul cablurilor descriu curenţii maximi pentru diferite valori şi aplicaţii ale acestora. Deşi punctul de topire al cuprului impune o limită amperajului conductorului, meterialele folosite de obicei la izolarea acestora posedă puncte de topire mult sub această temperatură; prin urmare, limitările amperajului iau practic în calcul limitele termice ale izolaţiei. Căderea de tensiune datorată rezistenţei excesive a conductorului este de asemenea un factor în alegerea tipului de conductori dintr-un circuit, dar această valoare se calculează prin metode specifice.
12.3 Siguranţe fuzibile
12.3.1 Definiţia şi scopul siguranţelor fuzibile
În mod normal, amperajul unui conductor reprezintă o limită a circuitului electric ce nu trebuie depăşită în mod intenţionat. Siguranţele fuzibile sunt proiectate tocmai pentru a acţiona în cazul unor astfel de „supra-curenţi”.
O siguranţă fuzibilă nu este altceva decât o un fir conductor scurt, proiectat astfel încât, în situaţia unui curent excesiv, acesta să se separe prin topire. *Siguranţele fuzibile se conectează tot timpul în serie cu componentul sau componentele ce necesită o protecţia la supra-curent*, astfel încât, în cazul deschiderii circuitului prin topirea siguranţei, curentul prin toate componentele sa scadă la zero. Desigur, o siguranţa fuzibilă conectată pe o ramură a unui circuit paralel, nu va afecta curentul prin celelalte ramuri.
În mod normal, firul conductor este acoperit de un înveliş protector pentru minimizarea pericolelor arcului electric în cazul deschiderii bruşte a circuitului. În cazul siguranţelor din locuinţă clasice, „liţele” sunt protejate de un patron din ceramică (poză). Siguranţele fuzibile folosite în cazul autoturismelor sunt transparente, astfel încât elementul fuzibil poate fi observat direct (poza).
Simbolul siguranţei fuzibile pe care îl vom folosi, este cel în formă de „S”, precum în figura alăturată.
Deoarece siguranţele fuzibile sunt proiectate pentru a se „defecta” în cazul în care limita maximă de curent din circuit este depăşită, este ideal ca acestea să poată fi îndepărtate şi înlocuite cu uşurinţă din circuit. Acest lucru înseamnă că ele vor fi introduse într-o cutie de siguranţe şi nu vor fi lipite sau prinse direct în circuit (poză).
12.3.2 Întrerupătoare automate
Întrerupătoarele automate sunt cele mai utilizate dispozitive pentru protecţia la supracurent. Aceste dispozitive sunt nişte întrerupătoare proiectate special pentru deschiderea automată şi oprirea alimentării cu energie electrică în cazul apariţiei unui supra-curent. Întrerupătoarele automate mici, precum cele din locuinţe, comerciale şi pentru iluminat, funcţionează pe bază termică. Acestea conţin o bandă bimetalică (o bandă subţirea formată din două metale puse cap la cap). La trecerea curentului din circuit prin aceasta, banda bimetalică se curbează sub acţiunea căldurii disipate. Atunci când forţa generată de bandă este suficient de mare (datorită supra-curentului ce o încălzeşte), mecanismul de întrerupere este acţionat iar întrerupătorul va deschide circuitul. Întrerupătoarele automate mai mari, sunt acţionate de forţa câmpului magnetic produs de conductoarele străbătute de curet din interiorul acestuia, sau pot fi acţionate de dispozitive exterioare (relee de protecţie) ce monitorizează curentul din circuit. În ambele cazuri, dispozitivul nu se distruge, ci doar se deschide; acesta poate fi reînchis prin acţionarea unei manete şi nu necesită nicio înlocuire precum esta cazul siguranţelor fuzibile (poza).
12.3.3 Consideraţii practice
Siguranţele fuzibile sunt catalogate după curentul maxim admis prin ele, şi anume, în amperi. Cu toate că funcţionarea acestora depinde de generarea căldurii în cazul curenţilor excesivi de către propria lor rezistenţa, acestea sunt construite astfel încât să contribuie cu o rezistenţă adtiţională neglijabilă în circuitul protejat. Acest lucru se relaizează printr-un fir conductor cât mai scurt posibil. La fel cum amperajul unui conductor nu depinde de lungimea sa, un fir folosit pentru construirea siguranţei fuzibile se va topi la un anumit curent indiferent de lungimea acestuia. Din moment ce lungimea nu reprezintă un factor pentru capacitatea maximă în curent a siguranţei, cu cât această lungime este mai mică, cu atât rezistenţa dintre cele două capete ale firului va fi mai mică.
Totuşi, trebuie luată în considerare şi situaţie în care o siguranţa fuzibilă se topeşte („sare”): capetele libere ale firului conductor vor fi separate în acest caz de un spaţiu liber şi o diferenţa de potenţial (tensiune) între acestea. Dacă firul nu este destul de lung, într-un circuit de tensiune înaltă, este posibilă ionizarea aerului dintre capete şi re-închiderea circuitului prin acest mediu.
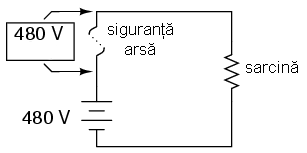
Atunci când siguranţa se arde, întreaga cădere de tensiune a sursei de alimentare se va regăsi pe aceasta, iar curentul din circuit va fi zero.
În cazul în care căderea de tensiune la bornele unei siguranţe fuzibile topite este suficient de mare, este posibilă apariţia arcului electric ce duce la apariţia unui curent în circuit, lucru pe care nu-l dorim.
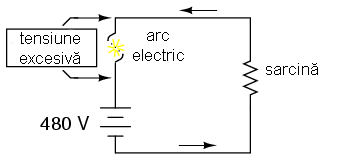
Prin urmare, siguranţele fuzible sunt catalogate atât în funcţie de curentul de „deschidere” cât şi în funcţie de tensiunea de străpungere a dielectricului existent între cele două capete dupa arderea acesteia.
12.3.4 Siguranţe fuzibile cu temporizare
La apariţia unui curent de 35 A printr-o siguranţă fuzibilă de 30 A, aceasta se poate arde instant sau poate prezenta o anumită durată de timp până la topirea conductorului metalic, în funcţie de tipul dispozitivului. Unele siguranţe sunt proiectate să se ardă extrem de repede, pe când altele necesită un timp mai indelungat de „deschidere”, sau chiar amânarea deschiderii, în funcţie de aplicaţie. Acestea din urmă poartă denumirea de siguranţe fuzibile lente, spre deosebire de celelalte, ce pot fi catalogate drept siguranţe fuzibile rapide.
O aplicaţie clasică a siguranţelor fuzibile lente este în cazul protecţiei motoarelor electrice, unde curenţii de pornire pot ajunge până la valori de zece ori mai mari decât curenţii normali de funcţionare. Dacă ar fi să folosim cele rapide, nu am putea porni motorul în primul rând, deoarece curenţii de pornire foarte mari ar duce la distrugerea imediată a siguranţei fuzibile. În cazul siguranţelor lente, elementul fuzibil este astfel proiectat încât să prezinte o masă mai mare (dar nu şi amperaj mai mare) decât o siguranţa rapidă, ceea ce înseamnă că încălzirea acestuia va dure un timp mai îndelungat, ajungând până la urmă la aceeiaşi temperatură, indiferent de valoarea curentului.
Pe de altă parte, există siguranţe fuzibile semiconductoare, proiectate pentru o deschidere extrem de rapidă în cazul apariţiei unei situaţii de supra-curent. Dispozitivele semiconductoare, precum tranzistorii, tind să fie foarte sensibile la supra-curenţi, prin urmare, în cazul acestora este nevoie de dispozitive de protecţie rapide în circuitele de putere mare.
12.3.5 Introducerea corectă în circuit a siguranţelor fuzibile
Siguranţele fuzibile trebuie poziţionate pe faza circuitului, în cazul circuitelor cu împământare. Scopul este oprirea curentului prin sarcini în cazul în care siguranţa se deschide. Putem face o comparaţie între cele două figuri alăturate, pentru a vedea diferenţa între utilizarea unei siguranţe pe fază şi utilizarea aceleaşi siguranţe pe neutru.
În acest caz, când siguranţa este introdusă în faza circuitului, la deschiderea acesteia, căderea de tensiune între oricare punct al sarcinii şi pământ va fi zero. Atingerea circuitului este sigură în acest caz, eliminând practic pericolul electrocutării.
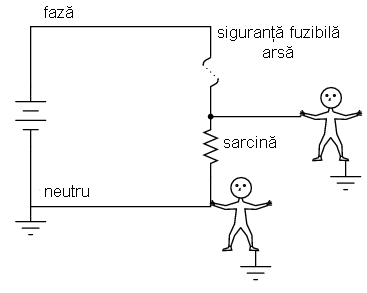
În cazul în care siguranţa fuzibilă este introdusă pe neutrul circuitului, în cazul deschiderii acesteia, va exista o tensiune periculoasă între oricare punct al sarcinii şi pământ. Atingerea circuitului în acest caz se poate dovedi periculoasă din punct de vedere al electrocutării.
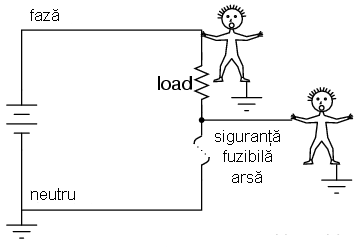
Indiferent dacă folosim siguranţe fuzible simple sau întrerupătoare automate, poziţionarea corectă a acestora în circuit se face conform celor spuse mai sus, şi anume: dispozitivul de siguranţa trebuie plasat pe partea de putere a circuitului şi nu conectat la pământ.
12.3.6 Observaţii
Cu toate că protecţia la supra-curent a circuitelor poate oferi într-o oarecare măsură o anumită siguranţă la electrocutare în anumite condiţii, trebuie înţeles faptul că aceste dispozitive nu sunt concepute în acest scop. Nici siguranţele fuzibile şi nici întrerupătoarele automate nu au fost proiectate cu scopul deschiderii în cazul electrocutării persoanei care atinge circuitul, ci, sunt proiectate pentru deschiderea în cazul supra-încălzirii conductorilor circuitului. Dispozitivele de protecţie la supra-curent, protejează în principal conductorii de la distrugere prin supra-incălzire şi a pericolelor asociate cu conductori foarte încinşi, şi în alt doilea rând, protejează anumite echipamente precum sarcini şi generatoare. Din moment ce valorile curenţilor necesari pentru electrocutare sunt mult mai mici decât curenţii normali ale sarcinilor din circuit, o condiţie de supra-curent nu indică neapărat un pericol de electrocutare, ci aceasta poate apărea chiar şi atunci când circuitul funcţionează la parametrii normali. Desigur, există dispozitive special concepute pentru protecţia la electrocutare (detectoare de curenţi de defect), dar aceste dispozitive sunt utilizate stric pentru acel scop şi nu au nico legătură cu protecţia conductorilor la supra-încălzire.
12.4 Rezistivitatea şi conductibilitatea electrică
Amperajul unui conductor, bazat pe potenţialul curentului de a distruge conductorul. nu este cea mai bună metodă de reprezentare a rezistenţei acestuia. Există situaţii în care căderea de tensiune creată de rezistenţa unui conductor în lungul acestuia duce la apariţia altor probleme decât evitarea incendiilor. De exemplu, să presupunem că proiectăm un circuit unde căderea de tensiune la bornele unui anumit component este extrem de importanţa şi nu trebuie să scadă sub o anumită limită. Dacă acest lucru se întâmplă, căderea de tensiune datorată rezistenţei conductorului poate duce la apariţia unei probleme tehnice a aplicaţiei în cauză.
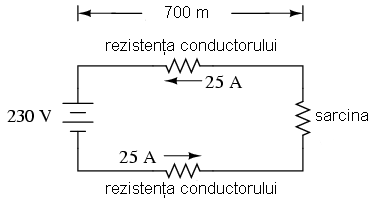
În circuitul alăturat, sarcina necesită o cădere de tensiune de cel puţin 220 V în cazul unei surse de tensiune este de 230 V. În acest caz, trebuie să ne asigurăm de faptul că rezistenţa conductorilor nu va genera o cădere de tensiune mai mare de 10 V în lungul acestora. Luând în considerare ambii conductori (dus şi întors), căderea de tensiune maximă admisă în lungul unui conductor este de 5 V. Utilizând legea lui Ohm, putem determina rezistenţa maximă admisă pentru fiecare conductor în parte:
R = E / I R = 5 V / 25 A R = 0,2 Ω
Ştim că lungimea fiecărui conductor este de 700 m, dar cum putem determina valoarea rezistenţei pentru o anumită lungime şi diametru al firului. Pentru acest lucru avem nevoie de o altă formulă, şi anume:
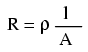
Prin urmare, rezistenţa electrică a unui conductor depinde de rezistivitatea acestuia, simbolizată prin litera grecească ρ (ro), de lungimea conductorului (l) şi de aria secţiunii transversale (A). Urmărind ecuaţia de mai sus, putem trage concluzia (deja ştiută) că rezistenţa conductorului creşte odată cu lungimea acestuia şi scade odată cu creşterea ariei secţiunii transversale. Rezistivitatea este o proprietate specifică unui anumit material de a se opune trecerii curentului prin acesta, iar unitatea sa de măsură este ohm-metru (Ω·m).
Rezistivitatea câtorva tipuri de materiale conductoare, la temperatura de 20o C este dată în tabelul alăturat. Putem observa că printre cele mai scăzute valori (ceea ce se traduce printr-o rezistenţa scăzută) o are cuprul, imediat după argint.
| Material | Element / Aliaj | 10-8 Ω·m |
|---|---|---|
| Nicrom | Aliaj | 112,2 |
| Nicrom V | Aliaj | 108,2 |
| Manganină | Aliaj | 48,21 |
| Constantan | Aliaj | 45,38 |
| Oţel | Aliaj | 16,62 |
| Platină | Element | 10,5 |
| Fier | Element | 9,61 |
| Nickel | Element | 6,93 |
| Zinc | Element | 5,90 |
| Molibden | Element | 5,34 |
| Tungsten | Element | 5,28 |
| Aluminiu | Element | 2,65 |
| Aur | Element | 2,21 |
| Cupru | Element | 1,67 |
| Argint | Element | 1,58 |
Revenind la circuitul din exemplul de mai sus, am calculat o rezistenţa de 0,2 Ω pentru o lungime de 700 m. Presupunând că materialul folosit este cupru (cel mai utilizat material pentru confecţionarea conductorilor electrici), putem determina aria secţiunii transversale necesare pentru conductorii din circuit:
R = ρ (l / A) A = ρ (l / R) A = 1,67 x 10-8 Ω·m (700 m / 0,2 Ω) A = 58,4 mm2
O secţiune transversală de 54,4 mm2, se traduce printr-un diametru al conductorului circular de 8,6 mm. Dacă luăm un tabel al conductorilor, putem observa că cea mai apropiată valoare mai mare decât 54,4 este 70 mm2, iar rezistenţa conductorului la o lungime de 1.000 m este de 0,268. Pentru exemplu nostru, la o lungime de 700 m, aceasta înseamnă o rezistenţa a conductorului de 0,182 Ω, sub valoarea maximă impusă de 0,2 Ω; conductorul ales este prin urmare potrivit pentru aplicaţia în cauză.
12.4.1 Conductibilitatea electrică
Conductibilitatea electrică, denumită şi conductivitate electrică, caracterizează capacitatea unui material de a permite deplasarea electronilor prin acesta. Simbolul matematic este σ (sigma), iar unitatea de măsură este Siemens pe metru (S·m-1). Practic, conductibilitatea electrică este inversa rezistivităţii electrice:
σ = 1 / ρ
12.5 Coeficientul de temperatură al rezistenţei
Tabelul rezistivităţilor diferitelor materiale, prezentat în secţiunea precedentă, s-a referit doar la temperatura de 20o. Prin urmare, dupa cum aţi putut bănui, rezistivitatea materialelor depinde de temperatură.
Valorile rezistenţelor conductorilor aflaţi la temperaturi diferite faţă de temperatura standard (20o tipic), din tabelul rezistivităţilor, se calculează printr-o altă formulă, şi anume:
R = Rref[1 + α(T - Tref)] unde, R = rezistenţa conductorului la temperatura „T” Rref = Rezistenţa conductorului la temperatura de referinţă, Tref, egală cu 20oC în mod uzual, dar poate fi şi 0oC α = coeficientul de temperatură al rezistenţei specific pentru materialul conductor T = temperatura conductorului (oC) Tref = temperatura de referinţa pentru care α este specificat
Se poate observa din relaţia de mai sus, că în cazul în care temperatura la care se află conductorul este exact temperatura de referinţă (20oC), atunci rezistenţa conductorului este exact rezistenţa de referinţă aşa cum este ea calculată din tabelul rezistivităţilor materialelor cu formula: R = ρl/A.
Constanta α, poartă numele de coeficientul de temperatură al rezistenţei, şi simbolizează variaţia rezistenţei cu temperatura; acest coeficient este specific fiecărui tip de material. Pentru metale pure, α este un număr pozitiv, ceea ce înseamnă că rezistenţa creşte odată cu creşterea temperaturii. Pentru carbon, siliciu şi germaniu, acest coeficient este negativ, ceea ce înseamnă că rezistenţa scade odată cu creşterea temperaturii. Pentru anumite aliaje, coeficient de temperatură al rezistenţei este foarte apropiat de valoarea zero, ceea ce înseamnă că rezistenţa aproape că nu se modifică odată cu variaţia temperaturii. În tabelul alăturat sunt prezentate câteva valori ale coeficientului α pentru câteva metale uzuale, pure sau aliaje, pentru temperatura de referinţă (Tref) de 20oC)
| Material | Element / Aliaj | α |
|---|---|---|
| Nichel | Element | 0.005866 |
| Fier | Element | 0.005671 |
| Molibden | Element | 0.004579 |
| Tungsten | Element | 0.004403 |
| Aluminiu | Element | 0.004308 |
| Cupru | Element | 0.004041 |
| Argint | Element | 0.003819 |
| Platină | Element | 0.003729 |
| Zinc | Element | 0.003847 |
| Aur | Element | 0.003715 |
| Oţel | Aliaj | 0.003000 |
| Nicrom | Aliaj | 0.000170 |
| Nicrom V | Aliaj | 0.000130 |
| Manganină | Aliaj | ± 0.000015 |
| Constantan | Aliaj | - 0.000074 |
12.5.1 Exemplu
Să luăm un circuit practic pentru a vedea efectele temperaturii asupra rezistenţei şi implicit asupra performanţei circuitului.
asupra rezistenţei şi asupra performanţei circuitului
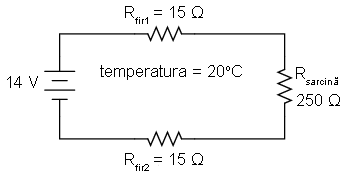
Rezistenţa totală a conductorilor din acest circuit este de 30 Ω (Rfir1 + Rfir2) la temperatura standard de 20oC. Folosind metoda tabelului pentru analiza circuitului, obţinem următoarele valori:
| Mărime | Fir1 | Fir2 | Sarcină | Total | Unitate |
|---|---|---|---|---|---|
| E | 0,75 | 0,75 | 12,5 | 14 | V |
| I | 50 m | 50 m | 50 m | 50 m | A |
| R | 15 | 15 | 250 | 280 | Ω |
La 20oC, obţinem o cădere de tensiune de 12,5 V la bornele sarcinii şi o cădere de tensiune totală de 1,5 V (0,75 V+ 0,75 V) în lungul conductoarelor datorită rezistenţei acestora. Dacă temperatura ar creşte la 35oC, putem vedea ce se întâmplă cu rezistenţele fiecărui conductor. Presupunând că materialul conductor este cuprul (α = 0,004041), obţinem următorul rezultat:
R = Rref[1 + α(T - Tref)] R = (15 Ω)[1 + 0,004041 (35o - 20o)] R = 15,9 Ω
Reanalizând circuitul de mai sus cu noile valori, putem vedea efectele creşterii temperaturii asupra circuitului.
| Mărime | Fir1 | Fir2 | Sarcină | Total | Unitate |
|---|---|---|---|---|---|
| E | 0,79 | 0,79 | 12,42 | 14 | V |
| I | 49,67 m | 49,67 m | 49,67 m | 49,67 m | A |
| R | 15,9 | 15,9 | 250 | 281,82 | Ω |
După cum se poate observa, tensiunea la bornele sarcinii a scăzut de la 12,5 V la 12,42 V, iar căderea de tensiune în lungul conductorilor a crescut de la 0,75 V la 0,79 V ca şi consecinţă a creşterii temperaturii. Chiar dacă variaţiile par mici, acestea se pot dovedi semnificative în cazul liniilor electrice de transport ce se pot intinde pe kilometri întregi între centralale electrice şi staţiile de transformare şi între staţiile de transformare şi consumatori.
12.6 Supraconductibilitatea
În cazul răcirii la temperaturi extrem de scăzute, temperaturi apropiate de zero absolut (aproximativ -273oC), rezistenţa conductorilor electrici scade la zero. Trebuie înţeles faptul că supraconductibilitatea nu este o extensie a tendinţei conductorilor de pierdere a rezistenţei cu descreşterea temperaturii, ci reprezintă o modificare cuantică bruscă a rezistivităţii de la o valoare finită la zero. Un material supraconductor prezintă o rezistenţă electrică de exact 0 Ω, nu doar o valoare foarte mică.
Acest fenomen a fost descoperit în 1911 de către H. Kamerlingh Onnes. Cu doar trei ani înainte, Onnes a dezvoltat o metodă de lichefiere a heliului, ce a permis existenţa unui mediu pentru supra-răcirea experimentală a diferitelor obiecte cu doar câteva grade peste nivelul de zero absolut. Investigând variaţia rezistenţei electrice a mercurului atunci când este încălzit la această temperatură joasă, Onnes a descoperit că rezistenţa acestuia scade la zero sub aproape de punctul de fierbere al heliului.
Nu este încă înţeles exact motivul pentru care materialele supraconductoare se comportă în acest fel. Una dintre teorii suţine că electronii se deplasează în grupuri (grupuri Cooper) prin conductor şi nu individual cum este cazul deplasării normale ale electronilor; acest lucru ar fi o legătură directă cu deplasarea lor fără frecare. Este interesant de menţionat faptul că şi în cazul fluidelor există un fenomen similar, denumit superfluditate, rezultând într-o curgere fără frecare a moleculelor, în special în cazul heliului lichid.
Supraconductibilitatea promite un comportament ieşit din comun al circuitelor electrice. Dacă rezistenţa conductorilor ar putea fi eliminată complet, nu ar mai există pierderi de putere sau ineficienţe în sistemele de putere datorate rezistenţelor parazite. Eficienţa motoarelor electrice ar putea creşte spre o eficienţă apropiată de 100%. Componente precum conedsatorul sau bobina, ale căror caracteristici sunt „stricate” de rezistenţa inerentă a conductorilor din care sunt construite, ar putea fi ideale în adevăratul sens al cuvântului. Deşi există astfel de aplicaţii, utilitatea lor practică este destul de scăzută datorită problemelor întâmpinate cu menţinerea temperaturilor extrem de scăzute.
12.6.1 Temperatura de tranziţie
Pragul de temperatură la care materialul trece din faza de conductibilitate normală la supraconductibilitate, poartă numele de temperatură de tranziţie, sau temperatură critică. Pentru supraconductorii „clasici”, temperatura de tranziţie se situează în jurul valorii de zero absolut. Ideal, un supraconductor ar trebui să funcţionezeze la temperatura camerei, sau cel puţin la o temperatură suficient de „ridicată” încât să poată fi menţinută cu echipamente de răcire relativ ieftine.
Temperaturile critice pentru câteva substanţe uzuale sunt prezentate în tabelul alăturat.
| Material | Element / Aliaj | Temperatura critică (oC) |
|---|---|---|
| Aluminiu | Element | -271,8 |
| Cadmiu | Element | -272,44 |
| Plumb | Element | -265,8 |
| Mercur | Element | -268,84 |
| Niobiu | Element | -264,3 |
| Toriu | Element | -271,63 |
| Staniu | Element | -269,28 |
| Titaniu | Element | -272,61 |
| Uraniu | Element | -272 |
| Zinc | Element | -272,09 |
| Niobiu / Staniu | Aliaj | -254,9 |
12.6.2 Efectul Meissner
Materialele supraconductoare interacţionează într-un mod interesant cu câmpurile magnetice. Atunci când se află în stare de supraconducţie, materialele supraconductoare tind să excludă toate câmpurile magnetice, fenomen cunoscut sub numele de efect Meissner. Totuşi, în cazul în care intensitatea câmpului magnetic depăşeşte o anumită valoare critică, materialul îşi va pierde proprietăţile supraconductoare, indiferent de temperatură. De fapt, prezeţa oricărui câmp magnetic în preajma acestora, tinde să scadă temperatura critică a materialului.
Acest lucru este încă un inconvenient din punct de vedere practic, din moment ce curentul electric prin orice conductor produce un câmp magnetic. Cu toate că un fir supraconductor nu posedă rezistenţă electrică la trecerea curentul, există o limită a volorii curentului prin acesta datorită limitei câmpului magnetic generat.
Lipsa rezistenţei electrice într-un circuit supraconductor conduce la efecte unice. Într-un astfel de circuit, menţinerea curenţilor mari este posibilă fără aplicarea niciunei tensiuni externe.
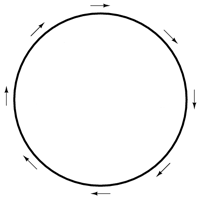
S-a demonstrat pe cale experimentală faptul că inele din materiale supraconductoare pot susţine curenţi prin ei ani la rând, fără aplicarea unei tensiuni. Practic, nu există o limită teoretică a perioadei de timp pentru care aceşti curenţi pot fi susţinuţi într-un circuit supraconductor. Acest efect pare a fi o formă de mişcare perpetuă. De fapt, nu există nicio lege a fizicii care să nu permită existenţă acestui tip de mişcare, ci doar o lege a fizicii care spune că un sistem nu poate genera mai multă energie decât consumă. În cel mai bun caz, o „maşină de mişcare perpetuă” poate doar să stocheze energie, nu să o şi genereze.
12.7 Străpungerea dielectricului
12.7.1 Definiţia străpungerii dielectrice
Electronii din interiorul atomilor materialelor dielectrice nu se pot deplasa la fel de uşor precum în cazul materialelor dielectrice. Totuşi, nici materialele dielectrice nu pot rezista unor tensiuni infinit de mari. *Atunci când tensiunea aplicată este suficient de mare, dielectricul va ceda până la urmă „presiunii” electrice iar deplasarea electronilor va avea eventual loc prin material*. Spunem în acest caz că a avut loc o străpungere a dielectricului. Faţă de conductori, unde curentul este direct proporţional cu tensiunea aplicată, atunci când valoarea rezistenţei este fixă, curentul printr-un dielectric este neliniar: pentru tensiuni aflate sub un anumit prag, nu va exista practic nici deplasare de electroni, dar, dacă tensiunea depăşeşte acest prag, curentul creşte extrem de rapid.
După străpungere, în funcţie de material, acesta poate să nu-şi mai recapete funcţia de dielectric (izolator), datorită modificării structurii sale moleculare. De obicei, există un „punct critic” ce desemnează locul prin care a avut loc deplasarea electronilor în momentul străpungerii.
12.7.2 Rigiditatea dielectrică
Grosimea materialului joacă un rol important în determinarea tensiunii sale de străpungere, tensiune cunoscută şi sub numele de rigiditate dielectrică. Alăturat este prezentat un tabel cu cele mai uzuale materiale folosite pe post de dielectric în cadrul circuitelor şi dispozitivelor electrice. Rigiditatea dielectrică este exprimată în MV / m (106V / m).
| Material | Rigiditatea dielectrică (MV / m) |
|---|---|
| Vid | 0,08 |
| Aer | 0,08 - 0,3 |
| Porţelan | 0,16 - 0,8 |
| Parafină | 0,8 - 1,2 |
| Ulei de transformator | 1,6 |
| Bachelită | 1,2 - 2,2 |
| Cauciuc | 1,8 - 2,8 |
| Şelac | 3,6 |
| Hârtie | 5 |
| Teflon | 6 |
| Sticlă | 8 - 12 |
| Mică | 20 |