< Curent continuu

2. Legea lui Ohm

2.1 Relaţia dintre tensiune, curent şi rezistenţă

Un circuit electric este format atunci când este construit un drum prin care electronii se pot deplasa continuu. Această mişcare continuă de electroni prin firele unui circuit poartă numele curent, şi adeseori este denimită „curgere”, la fel precum curgerea lichidului dintr-o ţeavă.

Forţa ce menţine „curgerea” electronilor prin circuit poartă numele de tensiune. Tensiunea este o mărime specifică a energiei potenţiale ce este tot timpul relativă între două puncte. Atunci când vorbim despre o anumită cantitate de tensiune prezentă într-un circuit, ne referim la cantiatea de energie potenţială existentă pentru deplasarea electronilor dintr-un punct al circuitului într-altul. Fără a face referinţa la două puncte distincte, termenul de „tensiune” nu are sens.

Electronii liberi tind să se deplaseze prin conductoare cu o anumită rezistenţă sau opoziţie la mişcare din partea acestora. Această opoziţia poartă numele de rezistenţă. Cantitatea de curent disponibilă într-un circuit depinde de cantitatea de tensiune disponibilă pentru a împinge electronii, dar şi de cantitatea de rezistenţă prezentă în circuit. Ca şi în cazul tensiunii, rezistenţa este o cantitate ce se măsoară între două puncte distincte. Din acest motiv, se folosesc termenii de „între” sau „la bornele” cand vorbim de tensiunea sau rezistenţă dintre două puncte ale unui circuit.

Pentru a putea vorbi concret despre valorile acestor mărimi într-un circuit, trebuie să putem descrie aceste cantităţi în acelaşi mod în care măsurăm temperatura, masa, distanţă sau oricare altă mărime fizică. Pentru masă, putem folosi „kilogramul” sau „gramul”. Pentru temperatură, putem folosi grade Fahrenheit sau grade Celsius. În următorul tabel avem unităţile de măsură standard pentru curentul electric, tensiune electrică şi rezistenţă:

Mărime	Simbol	Unitate de măsură	Prescurtare
Curent	I	Amper	A
Tensiune	E sau V	Volt	V
Rezistenţă	R	Ohm	Ω

„Simbolul” pentru fiecare mărime este litera din alfabet folosită pentru reprezentarea mărimii respective într-o ecuaţie algebrică. Asfel de litere standard sunt folosite adesea în discipline precum fizica şi ingineria, şi sunt recunoscute la nivel internaţional. „Unitatea de măsură” pentru fiecare cantitate reprezintă simbolul alfabetic folosit pentru a prescurta notaţia respectivei unităţi de măsură.

Fiecare unitate de măsură poartă numele unei personalităţi importante din domeniul electricităţii: amper-ul după Andre M. Ampere, volt-ul după Alessandro Volta, şi ohm-ul după Georg Simon Ohm.

Toate aceste valori sunt exprimate cu litere de tipar, exceptând cazurile în care o mărime (în special tensiunea sau curentul) este exprimată în funcţie de o durată scurtă de timp (numită valoarea „instantanee”). De exemplu, tensiunea unei baterii, fiind stabilă pe o perioadă lungă de timp, va fi simbolizată prin „E”, pe când tensiunea maximă atinsă de un fulger în momentul lovirii unei linii electrice va fi simbolizată cu litere mici, „e” (sau „v”) pentru a desemna această valoara ca existantă într-un anumit moment în timp. Aceeiaşi convenţie se foloseşte şi în cazul curentului, litera „i” fiind folosită pentru a reprezenta curentul instantaneu. Majoritatea mărimilor din curent continuu, fiind constante de-a lungul timpului, vor fi simbolizate cu litere mari (de tipar).

O mărime de bază în măsurătorile electrice, predată adesea la începutul cursurilor de electronică dar nefolosită mai târziu, este coulomb-ul, mărimea sarcinii electrice proporţională cu numărul de electroni în stare de dezechilibru. O sarcină de un coulomb este egală cu 6,25x10¹⁸ electroni. Simbolul mărimii sarcinii electrice este litera „Q”, iar unitatea de măsura, coulombul, este abreviata prin „C”. Vedem prin urmare faptul că unitate de măsură pentru deplasarea electronilor, amperul, este egal cu o cantitate de electroni egală cu 1 coulomb ce se deplasează printr-un punct al circuitului într-un interval de 1 secundă. Pe scurt, curentul este gradul de deplasare al sarcinii electrice printr-un conductor.

După cum am mai spus, tensiunea este mărimea energiei potenţiale pe unitatea de sarcină disponibilă pentru motivarea electronilor dintr-un punct în altul. Înainte de a putea da o definiţie exactă a „volt”-ului, trebuie să înţelegem cum putem măsura această cantitate pe care o numim „energie potenţială”. Unitatea generală pentru orice tip de energie este joule-ul, egal cu lucrul mecanic efectuat de o forţă de 1 newton pentru a deplasa un corp pe o distanţă de 1 metru. Definit prin aceşti termeni ştiinţifici, 1 volt este egal cu o energie electrică potenţială de 1 joule pe (împărţit la) o sarcină electrică de 1 coulomb. Asfel, o baterie de 9 volţi eliberează o energie de 9 jouli pentru fiecare coulomb de electroni ce se deplasează prin circuit.

Aceste simboluri şi unităţi pentru mărimile electrice vor fi foarte importante atunci atunci când vom începe să folosim relaţiile dintre ele în cadrul circuitelor. Prima, şi poate cea mai importantă, este relaţia dintre curent, tensiune şi rezistenţă, legea lui Ohm, descoperită de Georg Simon Ohm şi publicată în 1827 în lucrarea Die galvanishe Kette, mathematisch berabeitet (Analiza matematică a circuitului galvanic). Principala descoperire a lui Ohm a fost că, cantitatea de curent printr-un conductor metalic într-un circuit este direct proporţională cu tensiunea aplica asupra sa, oricare ar fi temperatura, lucru exprimat printr-o ecuaţie simplă ce descrie relaţie dintre tensiune, curent şi rezistenţă,

E = IR

În această expresie algebrică, tensiunea(E) este egală cu, curentul(I) înmulţit cu rezistenţa(R). Această formulă poate fi rescrisă sub următoarele forme, în funcţie de I,

I = E/R sau R = E/I

Să folosim acum aceste ecuaţii pentru a analiza circuitele simple:

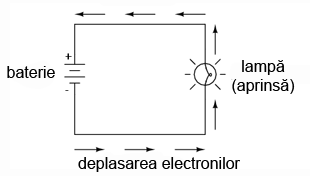
În circuitul de mai sus, există doar o singură sursă de tensiune (bateria), şi doar o singură rezistenţă (becul, neglijând rezistenţa datorată conductorilor). În această situaţie legea lui Ohm se poate aplica foarte uşor. În cazul în care cunoaştem două din cele trei variabile (tensiune, curent şi rezistenţă) din acest circuit, putem folosi legea lui Ohm pentru determinarea celei de a treia.

În acest prim exemplu, vom calcula cantitatea de curent (I) dintr-un circuit, atunci când cunoaştem valorile tensiunii (E) şi a rezistenţei (R):

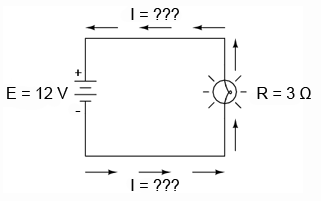
Care este valoarea curentului (I) din acest circuit?

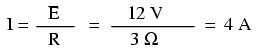
În al doilea exemplu, vom calcula valoarea rezistenţei (R) într-un circuit, atunci când cunoaştem valorile tensiunii (E) şi a curentului (I):

Care este valoarea rezistenţei becului în acest caz?

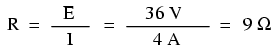
În ultimul exemplu, vom calcula valoarea tensiunii generate de baterie (E), atunci când cunoaştem valoarea curentului (I) şi a rezistenţei (R):

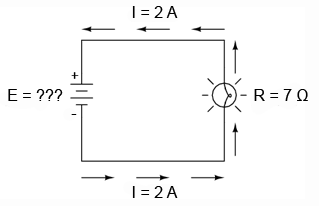
Care este valoarea tensiunii generate de baterie?

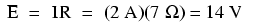
2.2 Puterea în circuitele electrice

Pe lângă tensiune şi curent, mai există o altă mărime a activităţii electronilor liberi din circuit: puterea. În primul rând trebuie să înţelegem ce este puterea, înainte de a o analiza într-un circuit

Puterea este mărimea lucrului mecanic ce poate fi efectuat într-o anumită perioadă de timp. Puterea este de obicei definită ca şi ridicarea unui corp (grutăţi) atunci când asupra acestuia acţionează forţa gravitaţiei. Cu cât corpul este mai greu şi/sau cu cât este ridicat la o înălţime mai mare, cu atât a fost efectuat mai mult lucru. Puterea măsoară cât de rapid a fost efectuată o cantitate standard de lucru.

În cazul automobilelor, puterea unui motor este dată în „cai putere”, termen inventat iniţial de producătorii motoarelor cu aburi ca şi mijloc de cuantificare a abilităţii maşinilor lor de a efectua lucru mecanic în relaţia cu cea mai utilizată sursă de putere din acele vremuri: calul. Puterea unui motor de automobil nu indică mărimea dealului ce-l poate urca sau ce greutate poate transporta, ci indică cât de repede poate urca un anumit deal sau trage o anumită greutate.

Puterea unui motor mecanic depinde atât de viteza motorului cât şi de cuplul ce se regăseşte pe arbore. Viteza arborelui unui motor se măsoară în rotaţii pe minut, sau r.p.m. Cuplul este cantitatea de forţă de torsiune produsă de motor şi se măsoară în Newton-metru (Nm). Dar nici viteza nici cuplul nu măsoară puterea unui motor.

Un motor diesel de tractor de 100 de cai putere, are o viteză de rotaţie mică, dar un cuplu mare. Um motor de motocicletă de 100 de cai putere, are o viteză de rotaţie foarte mare, dar un cuplu mic. Ambele produc 100 de cai putere, dar la viteze şi cupluri diferite. Ecuaţia pentru calcului cailor putere (CP) este simplă:

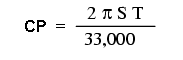
unde,

• S = viteza arborelui în r.p.m.
• T = cuplul arborelui în Nm
• π = 3.14 (constanta pi)

Putem observa că există doar două variabile în partea dreaptă a ecuaţiei, S şi T. Toţi ceilalţi termeni sunt constanţi: 2, π şi 5252, toate sunt constante (nu îşi modifică valoarea în funcţie de timp sau de situaţie). CP (cal putere) variază doar atunci când variază fie viteza fie cuplul şi nimic altceva. Putem rescrie ecuaţia pentru a arăta această relaţie:

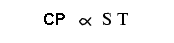
unde,

• ∝ înseamnă direct proporţional (adesea prescurtat d.p.)
• S şi T au semnificaţiile de mai sus

Doarece unitatea de măsură „cal putere” nu coincide exact cu viteza în rotaţii pe minut înmulţită cu cuplul în Newton-metru, nu putem spune că acesta este egal cu ST. Cu toate aceastea, „calul putere” este proporţional cu ST. Valoarea calului putere se va modifica în aceeiaşi proporţie cu produsul ST (atunci când acesta variază).

Pentru circuitele electrice, puterea este o funcţie (depinde) de curent şi tensiune. Nu este surprinzător faptul că această relaţie seamănă izbitor cu formula „proporţională” a calului putere de mai sus:

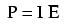
Totuşi, în acest caz, puterea (P) este exact egală curentului (I) înmulţit cu tensiunea (E), şi nu este doar proporţională cu aceast produs (IE). Când folosim această formulă, unitatea de măsură pentru putere este watt-ul, prescurtat prin litera „W”.

Trebuie înţeles faptul că nici tensiunea nici curentul nu înseamnă putere ele însele. Puterea este combinaţia celor două într-un circuit. Reţineţi că tensiunea este lucrul specific (sau energia potenţială) pe unitate de sarcină, în timp ce curentul este rata de deplasare a sarcinilor electrice printr-un conductor. Tensiunea (lucrul specific) este analog lucrului efectuat în ridicarea unei greutăţi atunci când asupra acesteia acţionează forţa gravitaţiei. Curentul (rata) este analog vitezei de ridicare a greutăţii respective. Împreună ca şi produs (înmulţire), tensiunea (lucru) şi curentul (rata) constituie puterea.

La fel ca în cazul unui motor diesel de tractor şi un motor de motocicletă, un circuit cu o tensiune mare şi curent scăzut, poate disipa aceeiaşi putere precum un circuit cu o tensiune scăzută şi curent mare. Nici valoarea tensiunii şi nici cea a curentului, nu pot să indice singure cantitatea de putere prezentă într-un circuit.

Într-un circuit deschis, acolo unde tensiunea este prezentă între bornele sursei iar curentul este zero, puterea disipată este şi ea egală cu zero, oricât de mare ar fi tensiunea. Din moment ce P=IE şi I=0, şi înmulţirea cu zero are ca şi rezultat tot timpul zero, înseamnă că şi puterea disipată în circuit trebuie să fie egală cu zero. Dacă am fi să construim un scurt-circuit cu ajutorul unei bucle din material superconductor (rezistenţă zero), am putea obţine o situaţia în care tensiunea de-a lungul buclei să fie egală cu zero, şi în acest caz puterea ar fi deasemenea zero, folosind logica de mai sus. (Despre superconductivitate vom vorbi într-un alt capitol).

Fie că măsurăm puterea în „cal putere” sau în „watt”, vorbim despre acelaşi lucru: ce cantitate de lucru poate fi efectuat într-o anumită perioadă de timp. Cele două unităţi nu sunt egală din punct de vedere numeric, dar exprimă acelaşi lucru. Relaţia dintre cele două puteri este:

1 CP = 745.7 W

Prin urmare, cele două motoare de 100 de cai putere de mai sus pot fi de asemenea notate cu „74570” de watti, sau „74.57” kW.

2.3 Calcularea puterii electrice

Am văzut formula pentru determinarea puterii într-un circuit electric: prin înmulţirea curentului (în amperi) cu tensiunea (în volţi) ajungem la „watti”. Să aplicăm această formulă unui circuit:

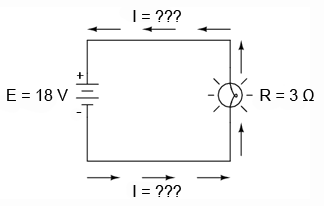
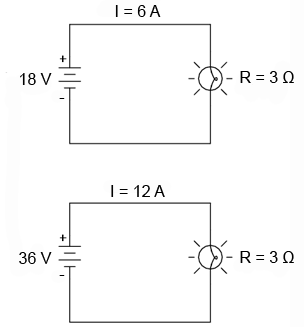
În circuitul de sus avem o baterie de 18 V, şi un bec cu o rezistenţă de 3 Ω. Folosind legea lui Ohm pentru determinarea curentului, obţinem:

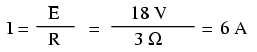
După ce am aflat valoarea curentului, putem lua această valoare şi să o înmulţim cu cea a tensiunii pentru a determina puterea:

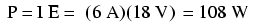
Prin urmare, becul degajează o putere de 108 W, atât sub formă de lumină, cât şi sub formă de căldură.

Să încercăm acum să luăm acelaşi circuit, dar să mărim tensiunea la bornele bateriei (schimbăm baterie) şi să vedem ce sa întâmplă. Intuiţia ne spune că va creşte curentul prin circuit pe măsură ce tensiunea bateriei creşte iar rezistenţa becului rămâne aceeiaşi. Şi puterea va creşte de asemenea:

Acum, tensiunea bateriei (tensiunea electromotoare) este de 36 V în loc de 18 V cât era înainte. Becul are o valoarea a rezistenţei tot de 3 Ω. Curentul este acum:

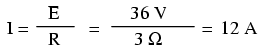
Trebuia să ne aşteptăm la acest lucru: dacă I = E/R, şi dublăm E-ul pe când R-ul rămâne acelaşi, curentul ar trebui să se dubleze. Întradevăr, asta s-a şi întâmplat; acum avem 12 A în loc de 6 A câţi aveam înainte. Să calculăm acum şi puterea:

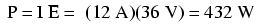
Observăm că puterea a crescut precum ne-am fi aşteptat, dar a crescut puţin mai mult decât curentul. De ce? Pentru că puterea este funcţie de produsul dintre tensiune şi curent, iar în acest caz, ambele valori, şi curentul şi tensiunea, s-au dublat faţă de valorile precedente, asfel că puterea a crescut cu un factor de 2 x 2, adică 4. Puteţi verifica acest lucru împărţind 432 la 108 şi observând că proporţia dintre cele două valori este întradevăr 4.

Folosind reguli algebrice pentru a manipula formulele, putem lua formula originală a puterii şi să o modificăm pentru cazurile în care nu cunoaştem şi tensiunea şi curentul:

În cazul în care cunoaştem doar tensiunea (E) şi rezistenţa (R):

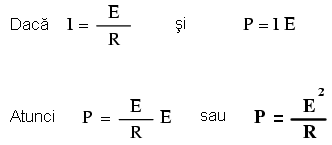
În cazul în care cunoaştem doar curentul (I) şi rezistenţa (R):

O notă istorică: James Prescott Joule este cel care a descoperit relaţia matematică între disiparea puterii şi curentul printr-o rezistenţă, nu Georg Simon Ohm. Această descoperire, publicată în 1843 sub forma ultimei ecuaţii (P = I²R), şi este cunoscută ca „Legea lui Joule”. Datorită faptului că aceste ecuaţii ale puterii sunt strâns legate de ecuaţiile legii lui Ohm legate de tensiune, curent şi rezistenţă (E=IR; I=E/R; R=E/I) sunt adeasea acreditate lui Ohm.

2.4 Rezistori

Datorită relaţiei dintre tensiune, curent şi rezistenţă în oricare circuit, putem controla oricare variabilă dintr-un circuit prin simplul control al celorlalte două. Probabil că cea mai uşor de controlat variabilă dintr-un circuit este rezistenţa. Acest lucru poate fi realizat prin schimbarea materialului, mărimii, formei componentelor conductive (ţineţi minte cum filamentul metalic subţire al unui bec crează o rezistenţă electrică mai mare decât un fir gros?)

Componente speciale numite rezistori sunt confecţionate cu singurul motiv de a crea o cantitate precisă de rezistenţă electrică la introducerea lor în circuit. Sunt construite din fir metalic sau de carbon în general, şi realizate asfel încât să menţină o rezistenţă stabilă într-o gamă largă de condiţi externe. Rezistorii nu produc lumină precum este cazul becurilor, dar produc căldură atunci când degajă putere electrică într-un circuit închis în stare de funcţionare. În mod normal, totuşi, scopul unui rezistor nu este producerea căldurii folositoare, ci pur şi simplu asigurarea unei rezistenţe electrice precise în circuit.

Simbolul rezistenţei pe care îl vom folosi în circuite este cel în formă de zig-zag:

Valorile rezistenţelor în ohmi sunt de obicei reprezentate printr-un număr adiacent, iar dacă într-un singur circuit sunt prezenţi mai mulţi rezistori, fiecare va fi notat cu R₁, R₂, R₃, etc. După cum se poate vedea, simbolurile pentru rezistenţă pot fi prezentate fie orizontal, fie vertical:

Rezistoarele reale nu seamănă deloc cu un zig-zag, ci sunt asemenea unor tuburi sau cilindrii cu câte un fir la fiecare capăt pentru conectarea lor în circuit. Mai jos sunt câteva exemple de rezistori de diferite tipuri şi mărimi:

Dacă ne luăm după aparenţa lor fizică, un simbol alternativ pentru rezistori este cel din figura de mai jos¹:

Rezistoarele pot de asemenea să fie cu rezistenţă variabilă, nu neapărat fixă. Această proprietate o putem întâlni în cadrul unui rezistor construit chiar pentru acest scop, sau o putem întâlni în cadrul unui component a cărui rezistenţă este instabilă în timp:

În general, ori de câte ori vedeţi simbolul unui component reprezentat cu o săgeată diagonală prin el, acel component are o valoarea variabilă şi nu statică (fixă). Acest simbol este o convenţie electronică standard.

Rezistoarele variabile trebuie să posede o modalitate de ajustare, fie un arbore rotitor sau un braţ ce poate fi mişcat pentru a varia valoarea rezistenţei electrice. Mai jos avem poza unor dispoizitive numite potenţiometre, ce pot fi folosite ca şi rezistori variabili:

Deoarece rezistori produc energie sub formă de căldură la trecerea curentului prin ei datorită frecării, aceştia pof fi împărţiţi în funcţie de cantitatea de căldură ce o pot susţine fără a se supra-încălzi şi distruge. Această categorie este specificată în „watti”. Majoritatea rezistorilor din aparatele electronice portabile sunt în categoria de 1/4 (0.25) watt sau mai puţin. Puterea unui rezistor este aproximativ proporţională cu mărimea sa: cu cât rezistorul este mai mare, cu atât mai mare este puterea sa. De menţionat şi faptul că rezistenţa (în ohmi) nu are deloc legătură cu mărimea!

Chiar dacă apariţia rezistorilor într-un circuit pare pe moment a nu avea niciun sens, aceştia sunt nişte dispozitive cu un rol extrem de folositor în cadrul circuitelor. Pentru că sunt atât de simpli şi de des utilizaţi în domeniul electricităţii şi a electronicii, vom dedica o bună bucată de vreme analizei circuitelor compuse doar din rezistenţe şi baterii.

În diagramele schematice, simbolul rezistorilor este adesea folosit pentru a indica un dispozitiv general dintr-un circuit electric ce transformă energia electrică primită în ceva folositor (bec, de exemplu). Orice asfel de dispozitiv non-specific într-un circuit electric poartă de obicei denumira de „sarcină”.

Pentru a rezuma ceea ce am spus până acum, vom analiza circuitul de mai jos, încercând să determinăm tot ceea ce putem cu ajutorul informaţiilor disponibile:

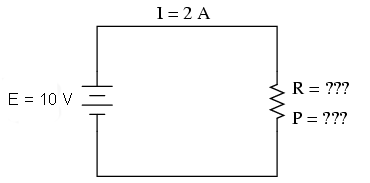
Tot ceea ce cunoaştem în acest circuit este tensiunea la bornele bariei (10 volţi) şi curentul prin circuit (2 amperi). Nu cunoaştem rezistenţa rezistorului în ohmi sau puterea disipată de acesta în watti. Folosindu-ne însă de ecuaţiile lui Ohm, putem găsi două ecuaţii ce ne pot oferi răspunsuri folosind doar cantitătile cunoascute, tensiunea, respectiv curentul:

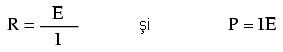
Introducând cantităţile cunoscute de tensiune (E) şi curent (I) în aceste două ecuaţii, putem determina rezistenţa circuitului (R), şi puterea disipată (P):

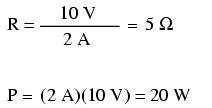
Pentru circuitul de faţă, în care avem 10 volţi şi 2 amperi, rezistenţa rezistorului trebuie şa fie de 5 Ω. Dacă ar fi să proiectăm un circuit pentru a opera la aceste valori, ar trebui să folosim un rezistor cu o putere de minim 20 de watti; în caz contrar, s-ar distruge din cauza supra-încălzirii.

2.5 Conducţie neliniară

Legea lui Ohm este un instrument simplu şi puternic pentru analiza circuitelor electrice, dar are şi unele limitaţii pe care trebuie să le înţelegem dacă vrem să o aplicăm cu succes circuitelor reale. Pentru majoritatea conductorilor, rezistenţa este o proprietate aproximativ constantă, neafectată de tensiune şi curent. Din acest motiv, considerăm rezistenţă majorităţii componentelor dintr-un circuit ca fiind constantă, astfel că tensiunea şi curentul sunt în relaţie directă unul cu celălalt.

De exemplu, în exemplu precedent cu becul de 3 Ω, am calculat curentul prin circuit împărţind tensiunea la rezistenţă (I=E/R). Cu o baterie de 18 volţi, curentul prin circuit a fost de 6 amperi. Dublând tensiunea bateriei la 36 de volţi, am dublat şi curentul la 12 volţi. Toate acest lucruri sunt evidente, atâta timp cât rezistenţa becului la deplasarea electronilor rămâne constantă la 3 Ω.

Totuşi, realitatea nu este atât de simplă. Unul din fenomenele prezentate într-un capitol viitor este cel al modificării rezistenţei odată cu modificarea temperaturii. Într-un bec incandescent, rezistenţa filamentului va creşte dramatic atunci când aceasta işi modifică temperatura de la cea a camerei la temperatura în stare de funcţionare. Dacă ar fi să mărim tensiunea furnizată într-un circuit real simplu, creşterea rezultată a curentului electric ar cauza creşterea temperaturii filamentul becului, creştere ce duce la creşterea rezistenţei acestuia, fapt ce face posibilă o nouă creştere a curentului prin circuit doar prin creşterea tensiunii furnizate de baterie. Prin urmare, tensiunea şi curentul nu se supun ecuaţiei simple „I=E/R”, deoarece rezistenţa filamentului unui bec nu rămâne stabilă odată cu modificarea curenţilor.

Fenomenul variaţiei rezistenţei cu temperatură este caracteristic majorităţii metalelor din care sunt confecţionate firele. Pentru majoritatea aplicaţiilor însă, aceste variaţii ale rezistenţei sunt suficient de mici încât sunt neglijabile (nu sunt luate în considerare). În cazul filamentelor becurilor, variaţia rezistenţei este destul de mare.

Acesta este doar un exemplu din domeniul neliniarităţii circuitelor electrice. Dar nu este nicidecum singurul. În matematică, o funcţie „liniară” este o funcţie reprezentată grafic printr-o linie dreaptă. Versiunea simplificată a circuitului simplu cu bec, cu o rezistenţă constantă a filamentului de 3 Ω, generează un grafic asemănător celui de jos:

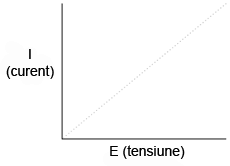
Linia dreaptă de pe grafic desemnează faptul că rezistenţa este stabilă pentru o varietate de tensiuni şi curenţi din circuit. Acest lucru se întâmplă însă doar într-un caz „ideal”. Fiindcă rezistorii sunt construiţi asfel încât rezistenţă lor să fie cât mai stabilă, se coportă aproximativ asemenea graficului de mai sus. Un matematician numeşte acest comportament „liniar”.

Un exemplu mai realist al unui circuit electric simplu cu bec, atunci când tensiunea la bornele bateriei variază într-un domeniu larg, este reprezentat prin graficul de mai jos:

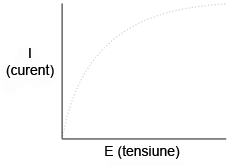
Acest grafic nu mai este o linie dreaptă. Acesta creşte brusc în partea stângă, odată cu creşterea tensiunii de la zero la o valoarea scăzută. Pe măsură ce tensiunea creşte, vedem o creştere din ce în ce mai mică a curentului; asfel că circuitul are nevoie de o creştere din ce în ce mai mare a tensiunii pentru a păstra o creştere egală şi constantă a curentului.

Dacă încercăm să aplicăm legea lui Ohm pentru determinarea rezistenţei acestui circuit folosind valorile curentului şi ale tensiunii din graficul de mai sus, ajungem la mai multe seturi de valori diferite. Putem spune că rezistenţa este neliniară, crescând cu creşterea tensiunii şi a curentului. Neliniaritatea este cauzată de efectul temperaturii ridicate a metalului ce compune filamentul becului.

Un alt exemplu de neliniaritate a curentului este prin gaze precum aerul. La temperaturi şi presiuni normale, aerul este un dielectric (izolator) eficient. Totuşi, dacă tensiunea dintre doi conductori separaţi printr-o porţiune de aer creşte suficient de mult, moleculele de aer se vor „ioniza”, iar electronii acestora se vor deplasa sub influenţa forţei generate de tensiunea ridicată dintre fire. Odată ionizate, aerul (şi alte gaze) devin bune conductoare de electricitate, permiţând curgerea electronilor. Dacă realizăm graficul curent-tensiune precum în circuitul precedent, putem observa foarte clar efectul neliniar al ionizării:

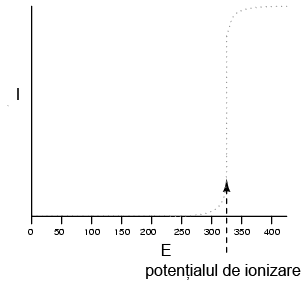
Graficul de mai sus este aproximat pentru o grosime a dielectricului (aer) de 1cm. O eventuală distanţă mai mare dintre cei doi conductori ar duce la un potenţial de ionizare mai ridicat, dar graficul curbei I/E ar rămâne similar: practic, nu există curent prin dielectric până în momentul atingerii potenţialului de ionizare, dar conducţia curentului este foarte bună după acest punct.

Acesta este şi motivul pentru care fulgerele există sub forma de şoc de scurtă durată şi sub o formă continuă de curgere a electronilor. Tensiunea formată între pământ şi nori (sau între diferiţi nori) trebuie să crească până la o valoare ce depăşeşte potenţialul de ionizare al golului de aer dintre cele două puncte. După atingerea acestui punct, aerul se ionizează suficient de mult pentru a permite curgerea substanţială a electronilor, iar curentul produs va exista prin aerul ionizat până în momentul în care sarcina electrică statică dintre cele două puncte se consumă. După scăderea sarcinii electrice până în punctul în care tensiunea scade sub un anumit punct de ionizare, aerul dintre cele două puncte (nor şi pământ) se dez-ionizează şi devine din nou un foarte bun dielectric (rezistenţă ridicată).

Multe materiale dielectrice solide posedă proprietăţi rezistive similare: rezistenţă extrem de mare la trecerea curentului electric sub o anumită tensiune critică, iar apoi, o rezistenţă mult diminuată la depăşirea acelei valori a tensiunii. Odată ce un material dielectric a trecut prin faza de străpungere (termenul folosit pentru acest fenomen), de cele mai multe ori acesta nu se reîntoarce la faza dielectrică precedentă aşa cum o fac majoritatea gazelor. Este posibil să se comporte ca şi un dielectric la tensiuni scăzute, dar valoarea pragului tensiunii de ionizare este mult sub valoarea iniţială, ceea ce duce la străpungeri mult mai uşoare pe viitor. Acesta este un mod de defectare des întâlnit în circuitele de tensiune înaltă: distrugerea izolaţie prin străpungere. Asemenea defecte pot fi detectate folosind aparate speciale de măurare a rezistenţei folosind tensiuni ridicate (peste 1000 V).

Există componente de circuit special concepute pentru proprietăţile lor rezistive neliniare; unul dintre acestea este varistorul. Confecţionat de obicei din oxid de zic sau carbură de siliciu, aceste dispozitive menţin o rezistenţă ridicată la bornele lor până în momentul atingerii unei tensiuni de „străpungere” (echivalentă cu „potenţialul de ionizare” a golului de aer), moment în care rezistenţa lor scade dramatic. Dar, faţă de străpungerea unui izolator, străpungerea unui varistor este repetabilă: adică, design-ul acesteia este de aşa natură încât permite străpungerile repetate fără apariţia distrugerii fizice a componentului.

Alte componente electrice posedă curbe de variaţie curent/tensiune şi mai ciudate. Unele dispozitive suferă o descreştere a rezistenţei odată cu creşterea tensiunii. Datorită faptului că panta curent/tensiune în acest caz este negativă, fenomenul este cunoscut sub denumirea de rezistenţă negativă.

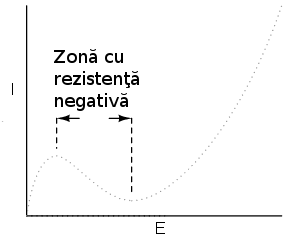
Pentru simplitatea expunerii totuşi, vom considera rezistenţele din circuit stabile în timp oricare ar fi condiţiile de funcţionare, exceptând faptul în care vom preciza altcumva. Aceasta a fost doar o mică parte din complexitatea lumii reale, pentru a nu lăsa impresia falsă că toate fenomenele electrice pot fi însumate sub câteva ecuaţii simple.

2.6 Conexiunea unui circuit

Până în acest moment am analizat circuite cu o singură baterie şi o singură rezistenţă fără a lua în calcul firele conductoare dintre componente, atâta timp cât am format un circuit complet. Contează lungimea firelor sau „forma” circuitului pentru calculele noastre? Să ne uităm aşadar la câteva configuraţii ale circitelor şi să aflăm:

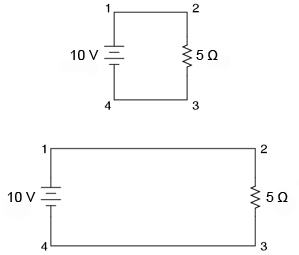
Atunci când conectăm două puncte dintr-un circuit printr-un fir conductor, presupunem de obicei că acele fire prezintă o rezistenţă neglijabilă. Prin urmare, ele nu contribuie într-o măsură hotărâtoare la rezistenţă totală a circuitului, iar singura rezistenţă pe care o luăm în calcul este rezistenţă componentelor din circuit. În circuitele de mai sus, singura rezistenţă este rezistenţă de 5 Ω a rezistoarelor, şi o vom considera doar pe aceasta în calculele noastre. În realitate, firele metalice au o anumită rezistenţă (precum şi sursele de tensiune!), dar acele rezistenţe sunt în general mult mai mici decât rezistenţa prezentă în celelalte componente din circuit încât pot fi neglijate. Excepţie fac firele din circuitele de putere (curenţi mari), unde chiar şi o rezistenţă foarte mică poate genera căderi de tensiune importante.

Dacă rezistenţă firelor conductoare este mică spre zero, putem considera punctele conectate din circuit ca fiind comune din punct de vedere electric. Punctele 1 şi 2 din circuitele de mai sus pot exista fizic foarte aproape unul de celălalt sau la o distanţă destul de mare pentru că, din punct de vedere al măsurătorilor tensiunii şi rezistenţei, acest lucru nu contează. Acelaşi lucru este valabil şi pentru punctele 3 şi 4. Este ca şi cum capetele rezistorilor ar fi ataşate direct la terminalele bateriei din punct de vedere al legii lui Ohm. Este bine de ştiut acest lucru, pentru că asta înseamnă că putem re-trasa circuitul, lungind sau scurtând firele după bunul nostru plac, fără a afecta funcţionarea circuitului în mod decisiv. Tot ceea ce contează este legarea componentelor unul de celălalt în aceeiaşi secvenţă.

Rezultă şi faptul că valorile tensiunii între seturi de puncte „comune” vor fi identice. Adică, tensiunea între punctele 1 şi 4 (la bornele bateriei), este aceeiaşi cu tensiunea dintre punctele 2 şi 3 (la bornele rezistorului). Să analizăm următorul circuit şi să vedem care sunt punctele comune:

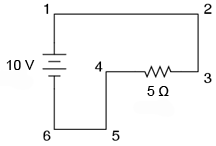
Aici avem doar două componente fără a lua în considerare şi firele: bateria şi rezistorul. Cu toate că firele au un drum mai încâlcit, ele formează un circuit şi există câteva puncte comune din punct de vedere electric în acest circuit, şi anume: punctele 1, 2 şi 3 pentru că aceastea sunt toate conectate între ele printr-un singur fir (fără alt component electric între ele). Acelaşi lucru este valabil şi pentru punctele 4, 5 şi 6.

Tensiunea între punctele 1 şi 6 este de 10 volţi, direct de la baterie. Dar, pentru că punctele 5 şi 4 sunt comune cu 6, iar punctele 2 şi 3 sunt comune cu 1, între aceste două grupe de puncte se regăsesc de asemenea 10 volţi:

• Între punctele 1 şi 4 = 10 volţi
• Între punctele 2 şi 4 = 10 volţi
• Între punctele 3 şi 4 = 10 volţi (direct la bornele rezistorului)
• Între punctele 1 şi 5 = 10 volţi
• Între punctele 2 şi 5 = 10 volţi
• Între punctele 3 şi 5 = 10 volţi
• Între punctele 1 şi 6 = 10 volţi (direct la bornele bateriei)
• Între punctele 2 şi 6 = 10 volţi
• Între punctele 3 şi 6 = 10 volţi

Din moment ce aceste puncte sunt conectate înpreună prin fire cu rezistenţă zero (ideală), căderea de tensine dintre aceste puncte este zero, indiferent ce cantitate de curent avem prin aceste puncte/fire. Dacă am fi să citim tensiunea între puncte comune, aceasta ar trebui să fie practic zero

• Între punctele 1 şi 2 = 0 volţi Punctele 1, 2, şi 3 sunt
• Între punctele 2 şi 3 = 0 volţi comune din punct de vedere electric
• Între punctele 1 şi 3 = 0 volţ
• Între punctele 4 şi 5 = 0 volţi Punctele 4, 5, şi 6 sunt
• Între punctele 5 şi 6 = 0 volţi comune din punct de vedere electric
• Între punctele 4 şi 6 = 0 volţi

Acest lucru are sens şi din punct de vedere matematic. Cu o baterie de 10 volţi şi un rezistor de 5 Ω, curentul va fi de 2 amperi. Rezistenţa firelor fiind zero, căderea de tensiune pe întregul circuit poate fi determinată cu ajutorul legii lui Ohm, asfel:

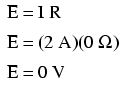
Pentru că punctele comune din punct de vedere electric dintr-un circuit au aceeiaşi tensiunea şi rezistenţă relativă, firele ce conectează aceste puncte sunt de obicei desemnate printr-o aceeiaşi notaţie. Asta nu înseamnă că punctele terminalelor au aceeiaşi denumire, ci doar firele de legătură. De exemplu:

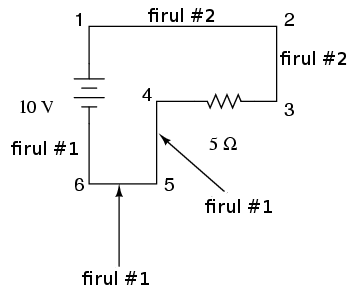
Punctele 1, 2 şi 3 sunt comune, prin urmare firul ce conectează punctele 1 şi 2 este notat asemenea (firul #2) firului ce conectează punctele 2 şi 3 (firul #2). Într-un circuit real, firul dintre punctele 1 şi 2 se poate avea culori şi mărimi diferite faţă de firul ce conectează punctele 2 şi 3, dar notaţia lor ar trebui să fie asemănătoare. Acelaşi lucru este valabil şi pentru firele ce conectează punctele 6, 5 şi 4.

Ne putem folosi de faptul că tensiunea dintre punctele comune este zero ca şi o metodă foarte bună de detectare a defectelor din circuit. Dacă măsor tensiunea din circuit dintre două puncte ce ar trebui să fie comune, aceasta ar trebui să fie zero. Dar dacă tensiunea citită este diferită de zero între aceste două puncte, atunci pot spune cu siguranţă că cele două puncte nu au o conexiune directă între ele (nu sunt comune), caz în care s-ar putea ca între cele două puncte, circuitul studiat să fie defapt (accidental) deschis.

2.7 Polaritatea căderilor de tensiune

Putem determina direcţia curgerii electronilor într-un circuit, urmărind drumul ce duce de la terminalul negativ (-) la cel pozitiv (+) al bateriei, singura sursă de tensiune din circuit. Observăm că electronii se deplasează contrar acelor de ceasornic, din punctul 6 spre 5, 4, 3, 2, 1 şi înapoi la 6.

În momentul în care curentul întâmpină rezistenţa de 5 Ω, se va înregistra o cădere de tensiune la capetele acesteia. Polaritatea acestei căderi de tensiune este minus (-) la punctul 4 şi plus (+) la punctul 3 (ţineţi minte, tensiunea este o mărime relativă între două puncte). Prin urmare, marcăm polaritatea căderii de tensiune la bornele rezistenţei cu aceste simboluri, folosind sensul real de deplasare al electronilor prin circuit, ceea ce înseamnă că borna pe unde curentul intră în rezistor este cea negativă, iar borna (capătul) pe unde curentul iese din rezistor este cea pozitivă.

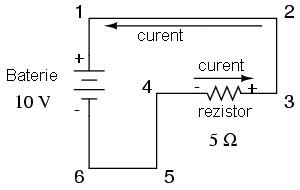
Între punctele 1 ( + ) şi 4 ( - ) = 10 volţi
Între punctele 2 ( + ) şi 4 ( - ) = 10 volţi
Între punctele 3 ( + ) şi 4 ( - ) = 10 volţi
Între punctele 1 ( + ) şi 5 ( - ) = 10 volţi
Între punctele 2 ( + ) şi 5 ( - ) = 10 volţi
Între punctele 3 ( + ) şi 5 ( - ) = 10 volţi
Între punctele 1 ( + ) şi 6 ( - ) = 10 volţi
Între punctele 2 ( + ) şi 6 ( - ) = 10 volţi
Între punctele 3 ( + ) şi 6 ( - ) = 10 volţi  

Chiar dacă pare puţin neinspirată realizarea unui tabel cuprinzând căderile de tensiune în întreg circuitul, acesta este un concept foarte important de ţinut minte, pentru că se va folosi la analiza circuitelor mult mai complexe, cuprinzând rezistenţe şi baterii multiple.

Trebuie înţeles faptul că polaritatea nu are nimic de-a face cu legea lui Ohm: nu vom introduce niciodată tensiuni, curenţi sau rezistenţe negative într-o ecuaţie a legii lui Ohm! Există într-adevăr alte principii electrice unde folosirea polarităţii (+ sau -) contează, dar nu este cazul legii lui Ohm.