< Curent continuu

6 Kirchhoff

6.1 Circuite divizoare de tensiune. Potenţiometrul

Să analizăm un circuit electric serie simplu, determinând căderile de tensiune pe fiecare rezistor:

Vom introducele valorile cunoscute precum şi cele ce le vom afla prin aplicarea formulelor într-un tabel ce cuprinde tensiunea (E), curentul (I) şi rezistenţa (R), precum şi suma acestora în întreg circuitul. Valorile sunt exprimate in volţi (V), amperi (A), respectiv ohmi (Ω).

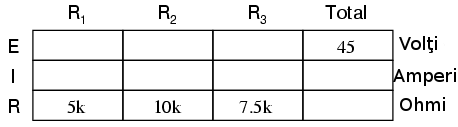
Folosind valorile individuale ale rezistenţelor, putem determina valoarea rezistenţei totale din circuit, cunoscând că valoarea totală este suma rezistenţelor individuale în cazul circuitelor serie:

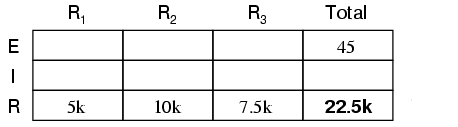
De aici, putem folosi legea lui Ohm (I=E/R) pentru determinarea valorii totale a curentului, ce va fi aceeiaşi cu valoarea curentului prin fiecare rezistor, curenţii fiind egali în toate componentele într-un circuit serie:

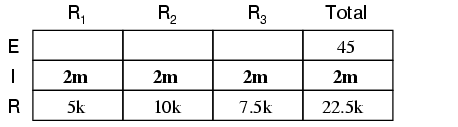
Cunoscând valoarea curentului (2 mA), putem folosi legea lui Ohm (E=IR) pentru calcularea căderilor de tensiune pe fiecare rezistor în parte:

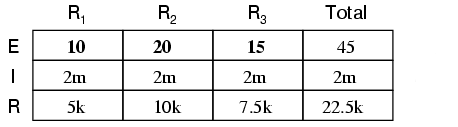
Putem observa că valoarea căderilor de tensiune pe fiecare rezistor este proporţională cu rezistenţa, datorită faptului că valoarea curentului este aceeiaşi prin toţi rezistorii. De asemenea, căderea de tensiune pe rezistorul R₂ este dublă faţă de căderea de tensiunea pe rezistorul R₁, la fel precum rezistenţa R₂ este dublă faţă de rezistenţa R₁.

Dacă ar fi să modificăm valoarea totală a tensiunii din circuit, vom vedea că această proporţionalitate a căderilor de tensiune rămâne constantă:

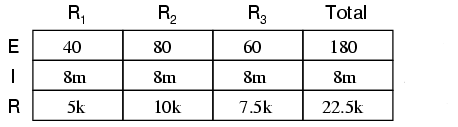
Căderea de tensiune pe R₂ este în continuare exact dublul căderii de pe R₁, în ciuda modificării tensiunii sursei. Proporţionalitatea căderilor de tensiune este strict în funcţie de valoarea rezistenţelor.

Devin aparent faptul că pe fiecare rezistor, căderea de tensiunea este o fracţiune fixă din valoarea tensiunii sursei. Tensiunea pe R₁ de exemplu, era 10 volţi atunci când valoarea tensiunii sursei era de 45 de volţi. Atunci când am crescut tensiunea bateriei până la 180 de volţi (de 4 ori mai mult), căderea de tensiune pe R₁ a crescut de asemenea de 4 ori (de la 10 la 40 de volţi). Raportul dintre căderea de tensiune pe R₁ şi căderea de tensiune totală a rămas însă aceeiaşi:

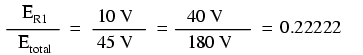
De asemenea, niciunul dintre raporturile căderilor de tensiune cu tensiunea sursei nu s-au schimbat:

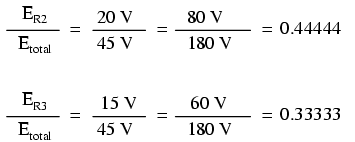
Din această cauză, un circuit serie poartă adesea numele de divizor de tensiune, pentru abilitatea sa de divizare a tensiunii totale în fracţii proporţionale cu o valoare constantă. Matematic, aceasta se poate exprima asfel:

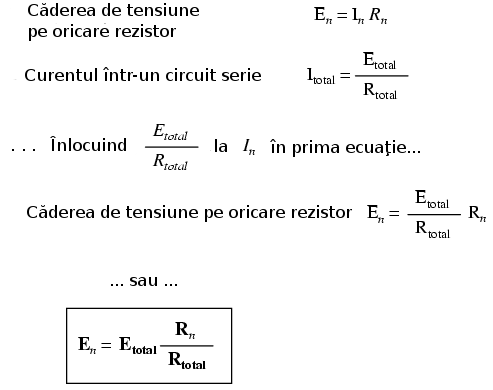
În cadrul unui circuit divizor de tensiune, raportul dintre rezistenţele individuale şi cea totală este acelaşi ca şi raportul dintre căderile de tensiune individuale şi tensiunea totală a sursei. Această formulă poartă denumirea de formula divizorului de tensiune, şi este o metodă mai rapidă de aflare a căderilor de tensiune într-un circuit serie faţa de folosirea repetată a legii lui Ohm

Folosind această formulă, putem re-analiza circuitul de mai sus în mai puţini paşi:

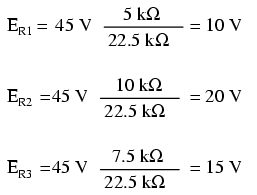
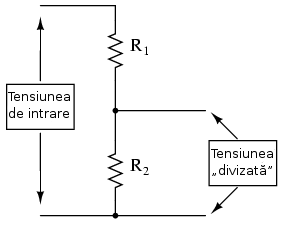
Circuitele divizoare de tensiune se folosesc acolo unde o combinaţie specifică de rezistori serie este folosită pentru a „diviza” tensiunea în cantiăţi precise (în cazul aparatelor de măsură, de exemplu).

Unul dintre dispozitivele folosite frecvent ca şi divizor de tensiune este potenţiometrul, ce este de fapt un rezistor cu un element mobil poziţionat cu ajutorul unei manete. Elementul mobil, denumit şi perie, face contact cu un material rezistiv dezizolat în oricare punct selectat manual:

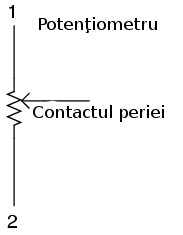
Pe măsură ce contactul periei este se apropie de terminalul 1 şi se îndepărtează de terminalul 2, rezistenţa spre terminalul 1 scade iar cea către terminalul 2 creşte. Dacă apropiem contactul de terminalul 2, vom obţine efectul contrar. Rezistenţa între cele două puncte (1 şi 2) este constantă indiferent de poziţia contactului periei.

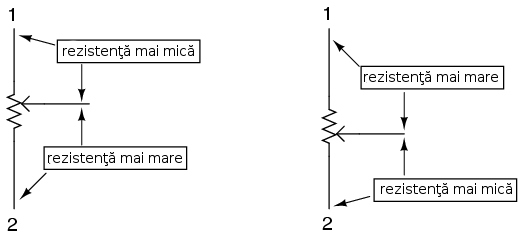
Mai jos sunt ilustrate două tipuri de potenţiometre, rotative şi liniare:

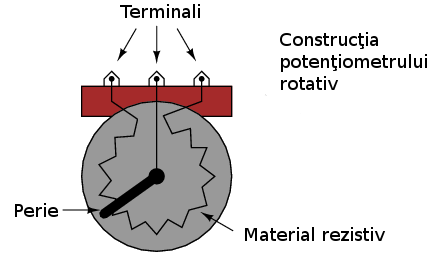
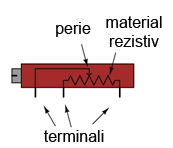
Pozele de mai jos reprezintă un potenţiometru rotativ real cu peria vizizibilă pentru o mai bună vizualizare. Axul ce deplasează peria este rotit în acest caz în sensul acelor de ceasornic aproape la maxim, asfel încât aproape atinge terminalul din stânga:

În acest caz, peria este rotită în sensul învers acelor de ceasornic, asfel încât aceasta se afla în cealaltă extremă:

Dacă aplicăm o tensiune constantă între cei doi terminali de la extremităţi, poziţia periei va „lua” doar o fracţiune din tensiunea aplicată, măsurată între contactul periei şi oricare dintre ceilalţi doi terminali. Valoarea acestei fracţii depinde în întregime de poziţia fizică a periei:

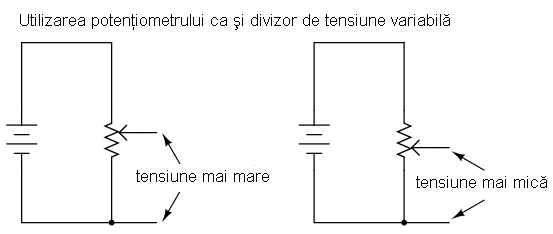
Ca şi în cazul unui divizor de tensiune fix, coeficientul de diviziune este strict o funcţie de rezistenţă şi nu depinde de valoarea tensiunii aplicate. Cu alte cuvinte, dacă maneta potenţiometrului este deplasată la exact jumătatea distanţei dintre cei doi terminali externi, căderea de tensiune între perie şi oricare dintre cei doi terminali este exact jumătate (1/2) din valoarea tensiunii aplicate, indiferent de valoarea aceteia sau de rezistenţa totală a potenţiometrului. Cu alte cuvinte, un potenţiometru acţionează precum un divizor variabil de tensiune, unde coeficientul de diviziune este stabilit de poziţia periei.

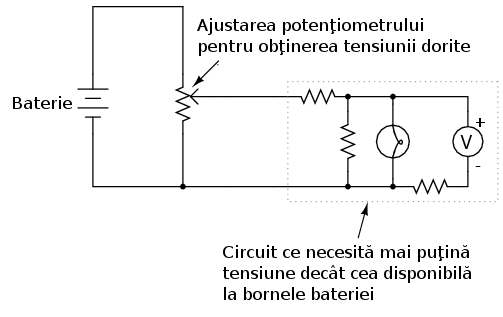
Această aplicaţie a potenţiometrului este una foarte folositoare pentru obţinerea unei tensiuni variabile cu ajutorul unei surse fixe de tensiune precum bateria. Dacă circuitul ce-l construim necesită o anumită valoare a tensiunii mai mică decât valoarea tensiunii la bornele bateriei, putem conecta terminalii externi ai potenţiometrului la baterie iar sarcina (bec, de exemplu) o conectăm între terminalul periei şi oricare dintre cei doi terminali externi:

6.2 Legea lui Kirchhoff pentru tensiune

Să luam un circuit serie cu trei rezistori şi să notăm punctele din circuit:

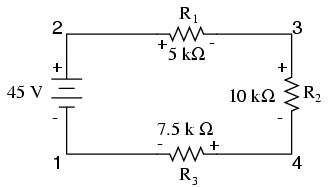
Dacă ar fi să conectăm un voltmetru între punctele 2 şi 1, sonda roşie la punctul 2 şi sonda neagră la punctul 1, voltmetru va indica valoarea de +45 V. În mod normal, semnul „+” nu este arătat, ci este implicit în cazul citirii aparatelor de măsură digitale.

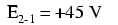
Când o tensiune este exprimată cu indice dublu („2-1” în cazul notaţiei „E_2-1”), înseamnă ca tensiunea este măsurată între cele două puncte. O tensiune exprimată prin „E_cg” ar însemna că tensiunea măsurată este cea indicată de un voltmetru cu sonda roşie conectată la punctul „c” şi sonda neagră la punctul „g”.

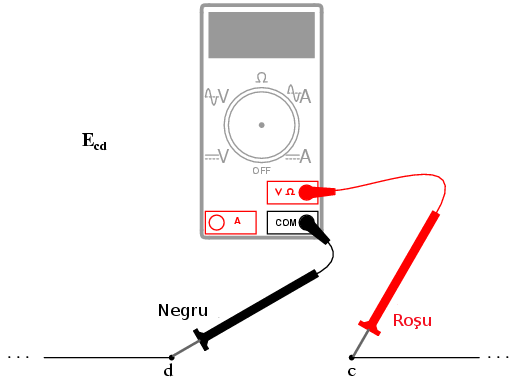
Dacă ar fi să luăm acelaşi voltmetru şi să măsurăm căderea de tensiune de pe fiecare rezistor, parcurgând circuitul în sensul acelor de ceasornic, cu sonda roşie în faţă şi cu cea neagră în spate, am obţine/citi următoarele valori:

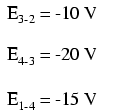
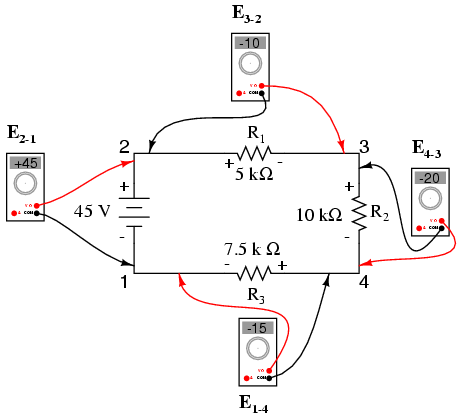
Suntem deja familiarizaţi cu conceptul general al circuitelor serie, si anume: suma căderilor de tensiune individuale este egală cu tensiunea aplicată. Dar, măsurând căderile de tensiune în acest fel şi ţinând cont de polaritatea („+” sau „-”) citirilor, descoperim o altă variantă a acestui principiu: suma tensiunilor măsurată în acest fel este zero:

Acest principiu este cunoscut sub denumirea de legea lui Kirchhoff pentru tensiune (descoperită în 1847 de către Gustav R. Kirchhoff, şi poate fi exprimat asfel:

„Suma algebrică a tuturor căderilor de tensiune dintr-o bulcă trebuie să fie egală cu zero”

Termenul de sumă algebrică este folosit pentru a desemna faptul că trebuie luate în considerarea semnele (polarităţile) tensiunilor din circuit pe lângă valorile acestora. Prin buclă se înţelege orice drum prin circuit ce începe şi se termină în acelaşi punct. În exemplul de mai sus, bucla s-a format între punctele 1-2-3-4-1, în exact această ordine. Nu contează punctul din care începem sau direcţie pe care o urmăm (în sensul acelor de ceasornic, sau invers), suma căderilor de tensiune va fi tot zero. Pentru a demonstra acest lucru, putem „modifica” bucla asfel (3-2-1-4-3):

Pentru o mai bună vizualizare, putem redesena circuitul serie de mai sus, asfel încât toate componentele să se regăsească pe aceeiaşi linie dreaptă:

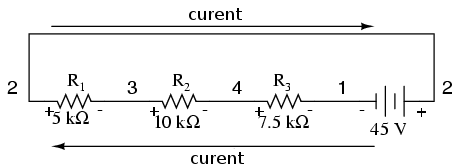
Este exact acelaşi circuit, doar că aranjamentul componentelor este diferit. Observaţi polaritatea căderilor de tensiune de pe rezistori în compoaraţie cu cea a bateriei: tensiunea bateriei este negativă în stânga şi pozitivă în dreapta, pe cât tensiunile la bornele rezistorilor sunt orientate în sens opus: pozitivă în stânga şi negativă în drepta. Aceasta pentru că rezistorii rezistă curegerii electronilor „împinşi” de baterie. Cu alte cuvinte, rezistenţa împotriva curgerii electronilor trebuie să fie direcţionată în direcţie opusă sursei de tensiune electromotoare.

Acestea sunt indicaţiile pe care un voltmetru introdus în circuit le-ar afişa (sonda neagră în stânga, cea roşie în dreapta):

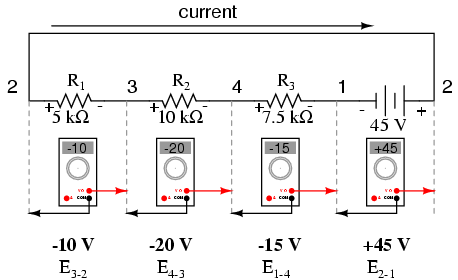
Dacă am fi să luăm acelaşi voltmetru pentru a citi căderile de tensiunea pentru combinaţiile componentelor din circuit începând cu R₁, putem observa adunarea algebrică a tensiunilor (spre zero):

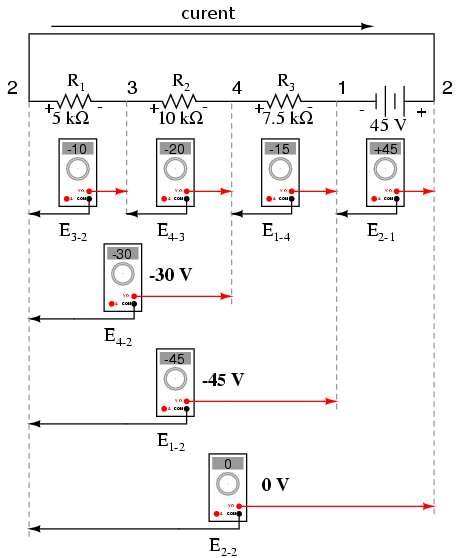
În cadrul măsurătorilor de mai sus, putem observa importanţa polarităţii căderilor de tensiune atunci când le adunăm. Citind rezultatele măsurătorilor tensiunii la bornele lui R₁, R₁–R₂ şi R₁–R₂–R₃ (folosim simbolul „–” pentru a desemna conexiunea „serie” între cei trei rezistori R₁R₂ şi R₃) vedem că suma căderilor de tensiune are valori tot mai mari (deşi negative), deoarece polaritatea căderilor de tensiune pe fiecare component are aceeiaşi orientare (stânga pozitiv, dreapta negativ). Suma căderilor de tensiune pe R₁, R₂ şi R₃ este de 45 de volţi, aceeiaşi cu tensiunea la ieşirea bateriei, cu observaţia că polaritatea bateriei este opusă faţă de cea a rezistorilor (stânga negativ, dreapta pozitiv) şi prin urmare rezultatul final este o măsurătoare de 0 volţi pe toate cele patru componente luate la un loc.

O un alt mod de a privi acest circuit este de a observa că partea stânga a circuitului(stânga rezistorului R₁: punctul 2) este conectat direct la partea dreapta a circuitului (dreapta bateriei: punctul 2), pas necesar pentru închiderea circuitului. Din moment ce aceste două puncte sunt conectate direct, acestea sunt electric comune şi prin urmare, căderea de tensiune dintre cele două trebuie să fie zero.

Legea lui Kirchhoff pentru tensiunie (prescurtat LKT) funcţionează pentru orice configuraţie a circuitului, nu doar pentru cele serie. Să vedem un exemplu pentru circuitul paralel prin urmare:

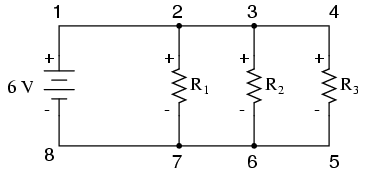
Fiind un circuit paralel, căderile de tensiune pe fiecare rezistor în parte sunt aceleaşi precum tensiunea sursei de alimentare: 6 volţi. Măsurând tensiunile în bucla 2-3-4-5-6-7-2, obţinem:

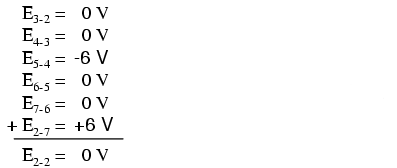
Observaţi notaţia căderii de tensiune totale (sumei) cu E_2-2. Din moment ce am început măsurătorile buclei la punctul 2 şi am terminat tot la punctul 2, suma algebrică a tuturor căderilor de tensiune va fi aceeiaşi cu tensiunea măsurată între acelaşi punct (E_2-2), care, desigur, trebuie să fie zero.

Faptul că acest circuit este paralel şi nu serie nu încurcă cu nimic aplicarea legii lui Krichhoff pentru tensiune. Din punctul nostru de vedere, întregul circuit ar putea să fie o „cutie neagră” - configuraţia componentelor să fie complet ascunsă şi să avem la dispoziţie doar un set de puncte unde să putem măsura tensiunea - şi legea lui Kirchhoff tot ar fi valabilă:

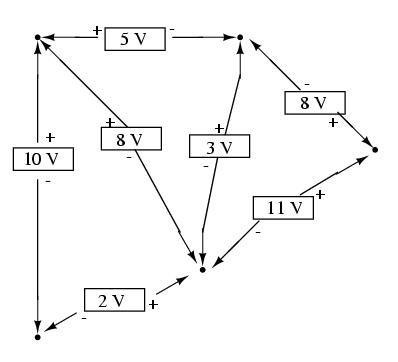
Dacă încercăm orice combinaţie de paşi, pornind de la oricare terminal în diagrama de mai sus, completând o buclă asfel încât să ajungem la punctul de unde am plecat, vom vedea că suma algebrică a tuturor căderilor de tensiune va fi tot timpul egală cu zero.

6.3 Circuite divizoare de curent

Să analizăm un circuit paralel simplu, determinând valorile curenţilor prin fiecare ramură, prin fiecare rezistor în parte:

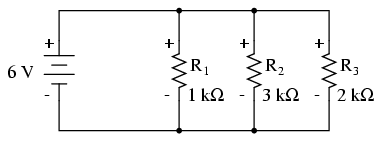
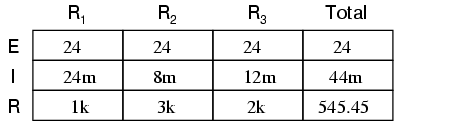
Cunoscând faptul că pe fiecare component în parte căderea de tensiune este aceeiaşi, putem completa tabelul tensiune/curent/rezistenţă asfel (mărimile sunt exprimate în volţi, amperi şi ohmi):

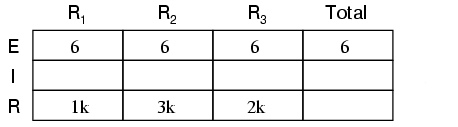
Folosind legea lui Ohm (I=E/R) putem calcula curentul prin fiecare ramură:

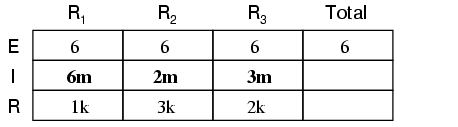
Ştiind că în circuitele paralele suma curenţilor de pe fiecare ramură reprezintă curentul total, putem completa tabelul cu valoarea totală a curentului prin circuit, 11 mA:

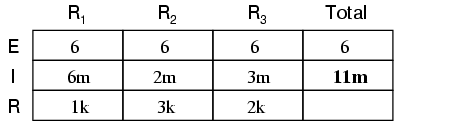
Ultimul pas este calcularea rezistenţei totale, folosind legea lui Ohm (R=E/I), sau folosind formula rezistenţelor în paralel; răspunsul va fi acelaşi:

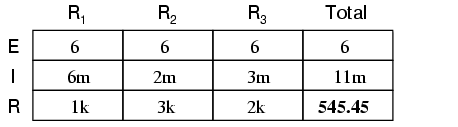
Ar trebui să fie evident deja faptul că prin fiecare rezistor curentul depinde de rezistenţa acestuia, ştiind că valoarea tensiunii prin toţi rezistorii este aceeiaşi. Această relaţie nu este una direct proporţională, ci invers proporţională. De exemplu, curentul prin R₁ este dublu faţă de curentul prin R₃, iar rezistenţa lui R₃ este de două ori cea a rezistorului R₁.

Dacă ar fi să schimbăm sursa de tensiune din acest circuit, am descoperi că (supriză!) acest raport nu se modifică:

Curentul prin R₁ este şi de data aceasta dublu curentului prin R₃, cu toate că valoarea tensiunii de alimentare (tensiunea bateriei) s-a modificat. Proporţionalitatea curenţilor între diferite ramuri ale circuitului depinde de rezistenţă.

De asemenea, precum era şi în cazul divizorilor de tensiune, curenţii ramurilor reprezintă fracţiuni fixe din curentul total. Cu toate că tensiunea sursei a crescut de patru ori, raportul dintre curentul ramurii şi curentul total a rămas acelaşi:

Din acest motiv, un circuit paralel este denumit adesea un divizor de curent pentru abilitatea sa de divizare a curentului total în fracţii. Cu ajutorul algebrei, putem determina o formulă pentru calculul curentului prin rezistorii paraleli, atunci când cunoaştem curentului total, rezistenţa totală şi rezistenţele individuale:

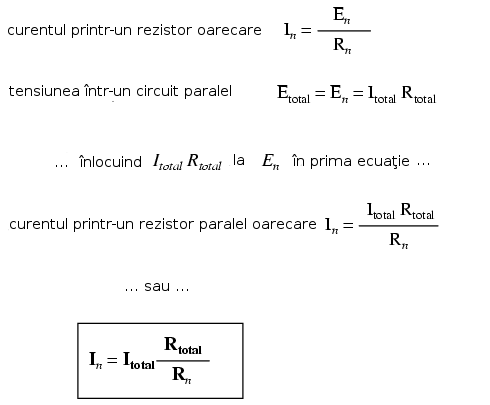
Raportul dintre rezistenţa totală şi rezistenţa individuală este acelaşi ca şi între curentul individual (pe ramură) şi cel total. Această formulă poartă denumirea de formula divizorului de curent, şi este o metodă mai scurtă de determinare a curenţilor prin ramură într-un circuit paralel atunci când se cunoaşte curentul total.

Folosind circuitul paralel original ca şi exemplu, putem re-calcula curentul prin ramuri folosind această formulă, dacă începem prin a cunoaşte valoarea totală a curentului şi a rezistenţei:

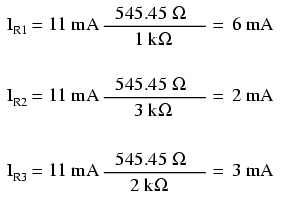
Dacă facem o comparaţie între cele două formule divizoare, putem observa că sunt extrem de asemănătoare. Putem observa totuşi, că în cazul divizorului de tensiune, raportul este R_n (rezistenţă individuală) la R_total, iar în cazul divizorului de curent, raportul este chiar inversi R_total la R_n:

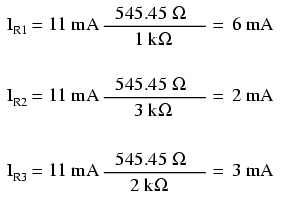
Este foarte uşor să încurcăm cele două ecuaţii prin inversarea raportului rezistenţelor. O modalitate simplă de memorare a formei corecte este să ţinem minte că ambele raporturi dintre cele două ecuaţii trebuie să fie un număr subunitar (între 0 şi 1). Până la urmă, acestea sunt ecuaţii divizoare nu multiplicatoare. Dacă raportul este inversat, vom obţine o valoare mai mare decât unu, prin urmare greşită. Cunoscând faptul că rezistenţa totală într-un circuit serie (divizor de tensiune) este tot timpul mai mare decât oricare dintre rezistenţe luate separat, putem să deducem că raportul corect este R_n/R_total. La fel, cunoscând faptul că rezistenţa totală într-un circuit paralel (divizor de curent) este tot timpul mai mică decât valoarea oricărei rezistenţe luate individual, putem să deducem raportul corect, R_n/R_total.

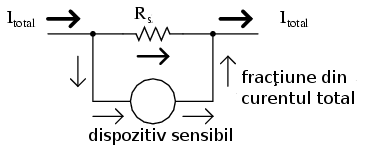
Circuitele divizoare de curent îşi găsesc aplicaţie (de exemplu) în circuitele de măsură, acolo unde o fracţie din curentul de măsurat trebuie să fie redirecţionat spre un dispozitiv sensibil de detecţie. Folosin formula rezistorului de curent, se poate afla valoarea exactă a rezistenţei folosită pe post de şunt pentru a „devia” cantitatea precisă de curent prin dispozitiv în orice situaţie.

6.4 Legea lui Kirchhoff pentru curent

Să considerăm următorul circuit paralel:

Calculând toate valorile tensiunilor şi curenţilor din acest circuit, obţinem:

În acest moment cunoaştem valorile curenţilor din fiecare ramură precum şi valoarea totală a curentului din circuit. Cunoaştem faptul că valoarea totală a curentului dintr-un circuit paralel trebuie să fie egală cu suma curenţilor de pe fiecare ramură, dar mai putem observa un principiu foarte important în acest circuit. Să observăm aşadar ce se întâmplă la fiecare nod (locul de întâlnire a cel puţin trei ramuri) din acest circuit:

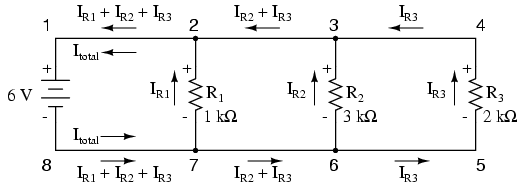
Pe ramura negativă de jos (8-7-6-5), la fiecare nod curentul principal se divide pe fiecare ramură succesivă spre rezistori. Pe ramura pozitivă de sus (1-2-3-4) curentul de pe fiecare ramură se „alătură” curentului principal. Dacă ne uităm mai atent la un anumit nod, precum 3, observă că valoarea curentului ce intră într-un nod este egală cu valoarea curentului ce părăseşte acel nod:

Avem doi curenţi care intră în nodul 3, din partea dreaptă şi de jos. Din partea stângă avem un singur curent care iese din nod, egal ca şi valoare cu suma celor doi curenţi care intră. Acest lucru este valabil pentru oricare nod, indiferent de numărul ieşirilor/intrărilor. Matematic, putem exprima această observaţie asfel:

I_intrare = I_ieşire

O altă formă uşor diferită dar echivaletă din punct de vedere matematic este următoarea:

I_intrare + (-I_ieşire) = 0

Pe scurt, legea lui Kirchhoff pentru curent sună asfel:

„Suma algebrică a tuturor curenţilor ce intră şi ies dintr-un nod trebuie să fie egală cu zero”

Adică, dacă notăm polaritatea fiecărui curent, cu „+” dacă intră într-un nod şi cu „-” dacă iese, suma lor va da tot timpul zero.

În cazul nodului 3 de mai sus, putem determina valoarea curentului ce iese din nod prin partea stângă folosind legea lui Kirchhoff pentru curent asfel:

Semnul negativ (-) pentru valoarea de 5 mA ne spune faptul că, curentul iese din acest nod, în contradicţie cu cei doi curenţi de 2 mA şi 3 mA ce sunt cu semnul pozitiv (+), şi prin urmare intră în nod. Cele două notaţii („+” şi „-”) pentru intrarea, respectiv ieşirea curentului din nod sunt pur arbitrare, atâta timp cât reprezintă semne diferite pentru direcţii diferite şi prin urmare putem aplica legeal lui Kirchhoff pentru curenţi.