< Electronică Digitală
7 Algebra booleana
7.1 Introducere şi scurt istoric
Regulile matematice sunt bazate pe limitele impuse asupra cantităţilor numerice particulare cu care avem de a face. Când spunem că 1 + 1 = 2, sau 3 + 4 = 7, presupunem din start că utilizăm un sistem de numeraţie zecimal. Regulile aritmetice pe care le considerăm de la sine înţelese - adevărate tot timpul şi în orice situaţie - depind de fapt de ceea ce înţelegem printr-un număr.
7.2 Aritmetica booleană
7.2.1 Numere binare şi numere booleene
Trebuie înţeles încă de la început faptul că numerele booleene nu sunt tot una cu numerele binare. Numerele booleene reprezintă un sistem matematic total diferit de cel al numerelor reale, pe când notaţia binare este doar atât: o notaţie alternativă a numerelor reale. Cele două sunt adesea confundate datorită faptului că utilizează aceleaşi cifre: 0 şi 1. Diferenţa constă în faptul că valorile booleene sunt limitate la un singur bit (fie 0, fie 1), pe când numerele binare pot fi compuse din mai mulţi biţi.
7.2.2 Adunarea booleană
Să începem aşadar capitolul de algebră booleană prin adunarea numerelor:
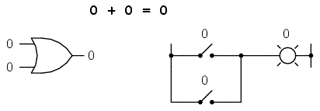
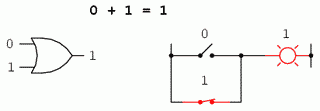
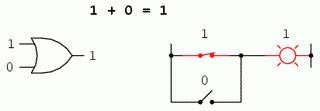
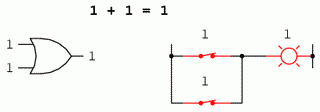
0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 1
Primele trei sume nu sunt deloc ieşite din comun din punct de vedere al operaţiei de adunare elementară. Ultima sumă în schimb, s-a dovedit a fi responsabilă de mai multă confuzie decât oricare alt element al electronicii digitale. Forma sa nu se supune princiilor de bază ale matematicii. Într-adevăr, aceasta contrazice principiile adunării numerelor reale, dar nu şi a numerelor booleene. În cadrul matematicii booleene există doar două valori posibile pentru oricare valoare şi pentru orice operaţie matematică: 0 sau 1. Nu există o valoare „2”. Din moment ce suma „1 + 1” nu poate fi 0, prin eliminare, această sumă trebuie să fie 1.
De asemenea, nu contează nici câţi termeni conţine suma. Să considerăm următoarele sume, de exemplu:
0 + 1 + 1 = 1 1 + 1 + 1 = 1 0 + 1 + 1 + 1 = 1 1 + 0 + 1 + 1 + 1 = 1
Revenind la primul set de ecuaţii, putem observa că aceste sume nu sunt altceva decât tabelul de adevăr al unei porţi logice SAU. Cu alte cuvinte, adunarea booleană corespunde funcţiei logice a porţii SAU, precum şi comutatoarelor conectate în paralel:
7.2.3 Scăderea şi împărţirea booleană
În cadrul matematicii booleene nu există noţiunea de scădere. Scăderea implică existenţa numerelor negative: 5 - 3 este identic cu 5 + (-3), de exemplu. Dar în algebra booleeană, valorile negative nu există (doar 0 şi 1).
De asemenea, nu există nici operaţie de împărţirea booleeană. Împărţirea nu este altceva decât o scădere compusă, la fel cum înmulţirea nu este altceva decât adunare compusă.
7.2.4 Înmulţirea booleană
Înmulţirea booleană este permisă, iar regulile sunt aceleaşi cu înmulţirea numerelor reale: orice număr înmulţit cu 0 este 0, şi orice număr înmultit cu 1 rămâne neschimbat:
0 x 0 = 0 0 x 1 = 0 1 x 0 = 0 1 x 1 = 1
Setul de ecuaţii ar trebui să vă fie cunoscute: sunt aceleaşi reguli ce se regăsesc în tabelul de adevăr al porţii ŞI. Cu alte cuvinte, înmulţirea booleană corespunde funcţiei logice a porţii ŞI, precum şi comutatoarelor conectate în serie:
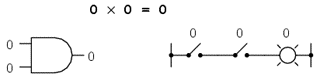
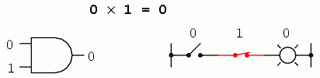
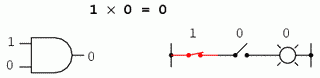
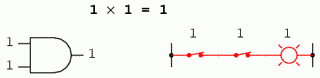
7.2.5 Variabile booleene şi complementul lor
La fel ca algebra „normală”, algebra booleană utilizează litere pentru desemnarea variabilelor. Dar, faţa de algebra „normală”, aceste variabile se trec tot timpul cu majuscule. Datorită faptului că există doar două stări posibile, fie 1, fie 0, fiecare variabilă posedă şi un complement: valoarea opusă a acesteia. De exemplu, dacă variabila „A” este 0, atunci complementul ei este 1. Complementul se specifică prin intermediul unei linii deasupra variabilei, astfel:

Sub formă scrisă, complementul lui „A” este desemnat prin „A-negat”. Câteodată se utilizează simbolul „'” pentru reprezentarea complementului (A'). De obicei însă, simbolul cu linie este mai folosit decât simbolul „'”. Motivele le vom afla puţin mai încolo.
Complementarea booleeană este echivalentă cu o poartă logică NU, sau cu un contact normal-închis:
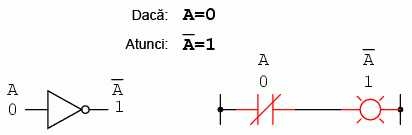
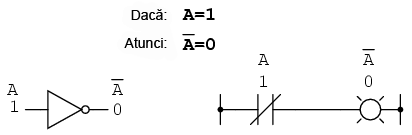
7. Identităţi algebrice booleene
7.3.1 Ce este o identitate
În matematică, o identitate este o afirmaţie valabilă pentru toate valorile posibile ale variabilei sau variabilelor implicate. Identitatea algebrică x + 0 = x, ne spune că suma dintre oricare variabilă (x) şi zero este egală cu variabila iniţială (x), indiferent de valoarea acesteia. Asemenea algebrei obişnuite, există identităti specifice algebrei booleene. Aceste identităţi sunt bazate pe cele două stări posibile ale variabilelor booleene (0 sau 1).
7.3.2 Identităţi aditive
Prima identitate booleană este suma unei variabile cu zero. Rezultatul este valoarea variabilei iniţiale. Această identitate nu este cu nimic diferită faţă de echivalentul algebric al numerelor reale:
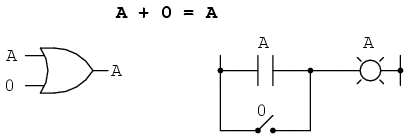
Indiferent de valoare lui A, ieşirea va fi tot timpul aceiaşi. Când A = 1, ieşirea va fi 1; când A = 0, ieşirea va fi 0.
Următoarea identitate este cu siguranţă diferită faţă de cele văzute în algebra obişnuită. Aici putem vedea că suma unei variabile cu 1 este 1:
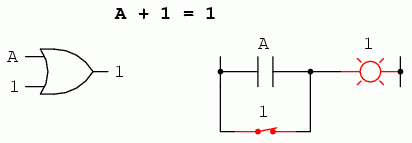
Indiferent de valoarea lui A, suma lui A cu 1 va fi tot timpul 1. Practic, ieşirea circuitului nu ţine cont de valoarea lui A, ci este fixată pe 1.
Următoare identitate este suma unei variabile cu ea însăşi. Practic, acest lucru înseamnă conectarea intrărilor unei porţi logice SAU şi activarea lor cu acelaşi semnal:
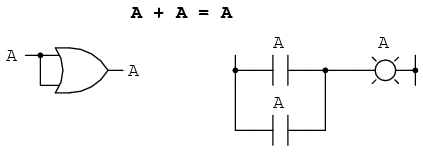
În algebra numerelor reale, suma a două variabile identice este dublul variabilei iniţiale (x + x = 2x). Dar în cadrul algebrei booleene nu exista „2”, ci numai 0 şi 1. Prin urmare, nu putem spune că A + A = 2A. Adunarea unei variabile cu ea însăşi este egală cu suma originală: 0 + 0 = 0 şi 1 + 1 = 1.
Dacă introducem conceptul de complement într-o identitate aditivă, putem vedea un efect interesant. Din moment ce între orice variabilă şi complementul acesteia trebuie să avem un 1, şi din moment ce suma oricărei variabile booleene cu 1 este 1, suma dintre o variabilă şi complementul ei trebuie să fie 1:
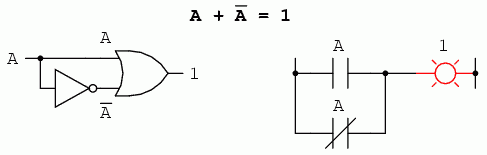
7.3.3 Identităţi multiplicative
La fel cum există patru identităţi booleene aditive (A + 0, A + 1, A + A şi A + A'), există şi patru identităti multiplicative: A x 0, A x 1, A x A şi A x A'. Dintre acestea, primele două nu sunt deloc diferite de identităţile echivalente ale algebrei numerelor reale:
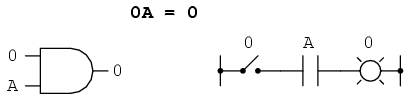
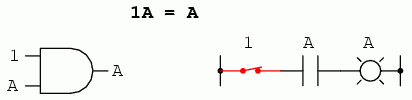
Cea de a treia identitate multiplicativă exprimă rezultatul unei variabile booleene înmulţită cu ea însăşi. În algebra numerelor reale, acest tip de produs reprezintă pătratul variabilei în cauză (3 x 3 = 32 = 9). Conceptul de „pătrat” implică existenţa valorii 2, valoare ce nu poate fi exprimată prin algebra booleană. Nu putem spune că A x A = A2. În schimb, produsul unei valori booleene cu ea însăşi este valoarea iniţială, din moment ce 0 x 0 = 0 şi 1 x 1 = 1:
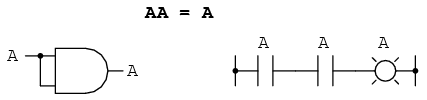
A patra identitate multiplicativă nu are echivalent în algebra numerelor reale, doarece utilizaează complementul variabilei. Acest concept este unic matematicii booleene. Din moment ce trebuie să avem o valoare de „0” între oricare variabilă şi complementul acesteia, şi din moment ce produsul oricărei valorii booleene cu 0 este 0, produsul dintre o variabilă şi complementul acesteia trebuei să fie 0:
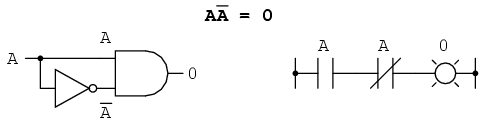
În concluzie, avem patru identităti booleene de bază pentru adunare şi patru pentru produs (multiplicative):

7.3.4 Identitatea complementului dublu
O altă identitate caracteristică complementului unei variabile este cea a complementului dublu: o variabilă inversată de două ori. Rezultatul complementării duble a unei variabile este valoarea booleană iniţială a variabilei. Acest lucru este similar înmulţirii cu -1 în algebra numerelor reale: un număr par de astfel de înmulţiri se anulează, iar rezultatul final este valoarea iniţială:
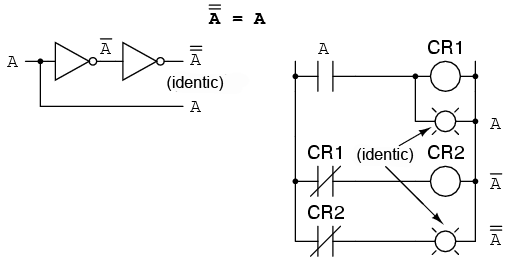
7.4 Proprietăţi algebrice booleene
Un alt tip de identitate matematică, denumită „proprietate”, descrie relaţia dintre variabilele unui sistem de numere.
7.4.1 Comutativitatea
Una dintre aceste proprietăţi poartă numele de comutativitate, şi se aplică atât adunării cât şi înmulţirii. Ceea ce ne spune comutativitatea este că, putem inversa ordinea variabilelor atât în cazul adunării, cât şi în cazul înmulţirii. Rezultatul expresiei rămâne neschimbat în ambele cazuri. Comutativitatea adunării arată astfel:
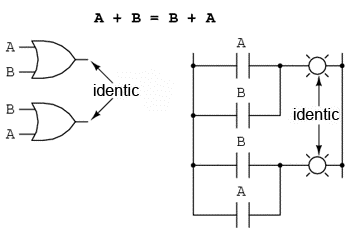
Comutativitatea înmulţirii:
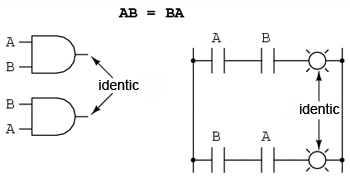
7.4.2 Asociativitatea
Această proprietate spune că putem asocia grupuri de sume sau înmulţiri, prin intermediul parantezelor, fară a modifica rezultatul ecuaţiilor. Şi în acest caz, asociativitatea se aplică atât adunării cât şi înmulţirii. Asociativitatea adunării:
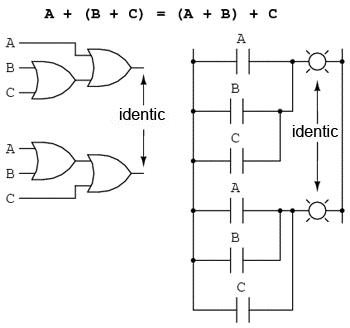
Asociativitatea înmulţirii:
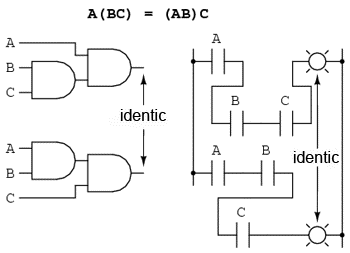
7.4.3 Distributivitatea
Proprietatea de distributivitate precizează modul de dezvoltare a unei expresii booleene formate din înmulţirea unei sume:
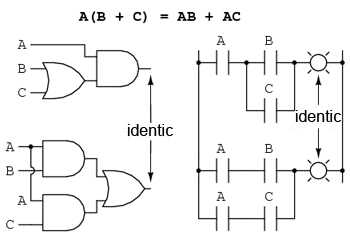
În concluzie, avem trei proprietăţi booleene de bază: comutativitatea, asociativitatea şi distributivitatea:
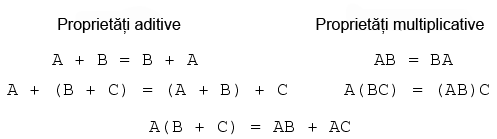
7.5 Reguli de simplificare booleană
Una dintre cele mai practice aplicaţii ale algebrei boolene constă în simplificarea circuitelor logice. Dacă transformăm funcţia logică a unui circuit sub formă booleană, şi aplicăm anumite reguli ecuaţiei rezultate, putem reduce numărul termenilor sau operaţiilor aritmetice necesare. Ecuaţia simplificată poată fi apoi transformată înapoi sub formă de circuit logic. Sub noua formă, circuitul logic realizează aceiaşi funcţie, dar cu mai puţine componente. Dacă un circuit echivalent poate fi realizat cu mai puţine componente, costurile de realizare şi de funcţionare vor scădea.
Identităţile şi proprietăţile exprimate în acest secţiunile precedente sunt foarte folositoare simplificării booleene. Toate regulie prezentate în această secţiune sunt specifice matematicii booleene.
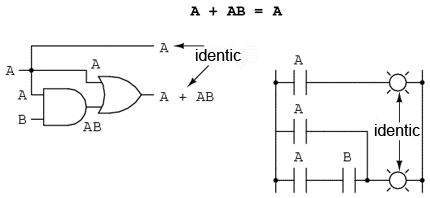
Această regulă poate fi demonstrată simbolic prin scoaterea termenului comun (A) în afara sumei. Aplicând apoi regulile A + 1 = 1 şi 1A = A, ajungem la rezultatul final:
A + AB = A(1 + B) = A(1) = A
Observaţi cum a fost aplicată regula A + 1 = 1 pentru reducerea termenului (B + 1) la 1. Când aplicăm o regulă precum „A + 1 = 1”, exprimată prin intermediul literei „A”, nu înseamnă că aceasta se aplică doar expresiilor ce conţin „A”. A-ul din această expresie exprimă faptul că aceasta se aplică oricărei variabile sau colecţii de variabile booleene.
De exemplu, expresia booleeană ABC + 1 se reduce tot la 1 prin intermediul aplicării identităţii A + 1 = 1. În acest caz, termenul standard „A” din definiţia identităţii reprezintă întregul termen „ABC” al expresiei de mai sus.
Următoarea regulă este aproximativ similară cu prima. Practic, ea este destul de diferită, iar demonstraţia este puţin mai dificilă:
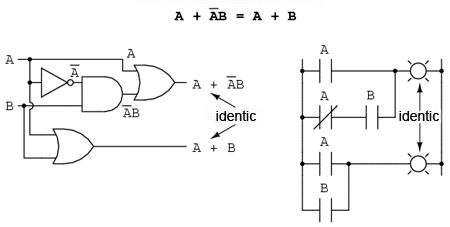
Pentru început, dezvoltăm termenul A, folosind regula precedentă (A + AB = A). Scoatem termenul B în afara celei de a doua sume, şi aplicăm apoi identitatea A + A' = 1. La sfârşit, nu ne mai rămne decât să aplicăm identitatea 1A = A pentru obţinerea rezultatului final:
A + A'B = A + AB + A'B = A + B(A + A') = A + B(1) = A + B
O altă regulă implică simplificarea expresiei unui produs de sume:
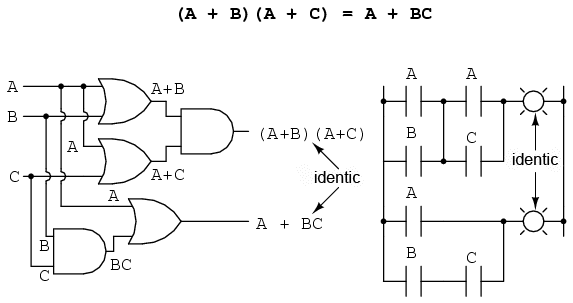
Pentru a demonstra această relaţie, realizăm pentru început înmulţirea celor două sume. Aplicăm apoi identitatea AA = A, apoi regula A + AB = A primilor doi termeni. Şi, în sfârşit, aplicăm aceiaşi regulă, A + AB = A primilor doi termeni a expresiei rezultate. Rezultatul este conform expresiei de mai sus:
(A + B)(A + C) = AA + AC + AB + BC = A + AC + AB + BC = A + AB + BC = A
Pe scurt, acestea sunt cele trei reguli ale simplificării booleene:
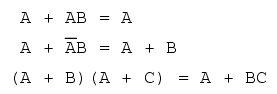
7.6 Simplificarea circuitelor logice
7.6.1 Simplificarea circuitelor cu porţi logice
Să începem cu un circuit logic cu porţi ce necesită o simplificare. Presupunem că intrările A, B şi C sunt asigurate de comutatoare, senzori sau alte porţi logice. Originea acestor semnale nu este importantă din punct de vedere al simplificării.
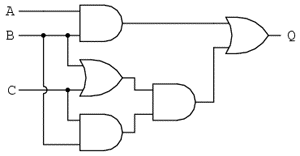
Scrierea expresiei booleene
Primul pas al simplificării constă în scrierea expresiei booleene pentru acest circuit. Acest pas este cel mai uşor de realizat dacă scriem sub-expresii pentru ieşirea fiecărei porţi, corespunzător semnalelor de intrare. Este bine să reamintim faptul că porţile SAU sunt echivalente adunării booleene, iar porţile ŞI sunt echivalente înmulţirii booleene. Să scriem aşadar sub-expresii la ieşirea primelor trei porţi:
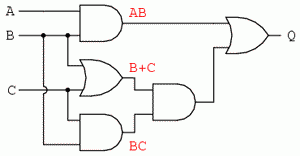
Scriem apoi sub-expresiile următoarelor seturi de porţi. În cazul de faţa, avem doar o singură poartă pe nivelul următor:
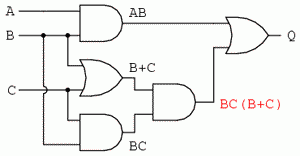
Şi, în sfârşit, ieşirea (Q) circuitului logic este egală cu următoarea expresie:
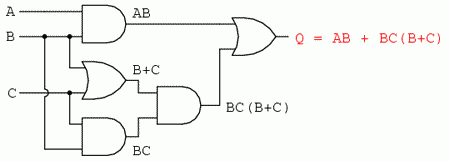
Simplificarea expresiei booleene
Acum că avem o expresie booleenă, următorul pas este aplicarea regulilor algebrei booleene pentru reducerea expresiei de mai sus la forma ei cea mai simplă. Reamintim faptul că cea mai simplă formă este aceas formă care necesită cele mai puţine porţi logice pentru implementarea ei.
Prin urmare, expresia AB + BC(B + C) poate fi redusă astfel: la primul pas realizăm înmulţirea termenilor; aplicăm apoi identitatea AA = A termenilor doi şi trei; aplicăm identitatea A + A = A termenilor doi şi trei rezultaţi; scoatem termenul comun B în faţa:
AB + BC(B + C) = AB + BBC + BCC = AB + BC + BC = AB + BC = B(A + C)
Expresia rezultată, B(A + C), este mult mai simplă decât cea originală. Ea realizează însă aceiaşi funcţie. Dacă vreţi să verificaţi acest lucru, puteţi construi un tabel de adevăr pentru ambele expresii, Determinaţi apoi rezultatul Q (ieşirea circuitului) pentru toate cele opt combinaţii posibile dintre A, B şi C pentru ambele circuitele. Cele două tabele trebuie să fie identice.
Evaluarea expresiei booleene rezultate
Următorul pas constă în generarea unei scheme logice folosind această expresie booleeană simplificată. Pentru realizarea acestui lucru, evaluăm expresia urmând ordinea matematică a operaţiilor (înmulţirea înainte adunării, operaţiile din interiorul parantezelor înaintea celorlalte). La fiecare pas vom adăuga o nouă poartă. Porţile sau sunt echivalente cu adunarea booleană, iar porţile ŞI sunt echivalente operaţiei de înmulţirea booleană. În exemplul de faţa, începem construirea circuitului cu sub-expresia „A + C”, expresie ce nu este altceva decât o poartă SAU:
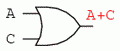
Următorul pas în evaluarea expresiei B(A + C) constă în înmulţirea (poartă ŞI) semnalului B cu ieşirea porţii precedente (A + C):
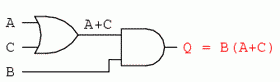
Evident, acest circuit este mult mai simplu decât cel original, având doar două porţi logice în loc de cinci. O astfel de reducere a numărului de componente duce la viteze de funcţionare crescute (timpul de propagare a semnalului de la intrare la ieşire este mai scurt), consum de energie mai scăzută, cost mai mic şi o fiabilitate crescută.
7.6.2 Simplificarea circuitelor cu relee electromecanice
Circuitele cu relee electromecanice pot profita foarte mult de pe urma simplificării booleene. De obicei, acestea sunt mai lente, consumă mult mai multă energie, costă mai mult, iar durata de viaţă medie este mai scurtă decât cea a porţilor logice semiconductoare. Să considerăm aşadar exemplul de mai jos:
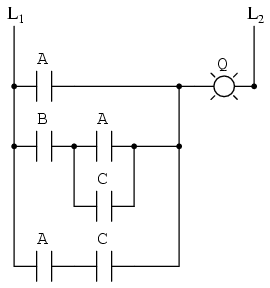
Scrierea expresiei booleene
Primul pas al reducerii acestui circuit la forma cea mai simplă este, din nou, transformarea circuitului sub forma unei expresii booleene. Cea mai simplă metodă de realizare a acestui lucru este asemănătoare cu metoda reducerii unui circuit rezistiv serie-paralel la o singură rezistenţă. De exemplu, să considerăm circuitul rezistiv de mai jos, cu rezistorii aranjaţi asemeni contactelor circuitului precedent.
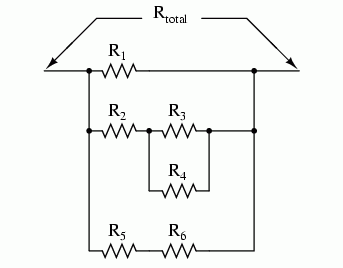
Formula corespunzătoare reducerii acestui circuit la o rezistenţă echivalenta, este următoarea:
Rtotal = R1 / [(R3 / R4) – R2] / (R5 – R6)
Contactele paralele sunt echivalente cu adunarea booleeană, iar contactele serie cu înmulţirea booleeană. Expresia booleenă a circuitului cu relee de mai sus se scrie urmând aceleaşi reguli care se regăsesc în cazul rducerii circuitelor serie-paralel la o rezistenţa totală echivalentă. Simplificarea ne este uşurată dacă scriem sub-expresii booleene la stânga fiecărei linii în parte:
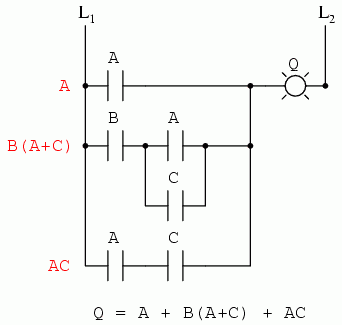
Acum că avem o expresie booleană, tot ceea ce trebuie să facem este să aplicăm regulile de simplificare pentru a aduce expresia la forma ei cea mai simplă (formă ce necesită cele mai puţine relee pentru implementarea fizică).
Paşii sunt următorii: extindem termenul B(A + C); aplicăm regula A + AB = A primilor doi termeni; aplicăm regula A + AB = A primului termen şi termenului al treilea:
A + B(A + C) + AC = A + AB + BC + AC = A + BC + AC = A + BC
După cum putem vedea, circuitul redus este mult mai simplu decât originalul, dar funcţia logică pe care o îndeplineşte este neschimbată:
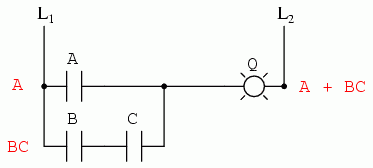
7.7 Funcţia SAU-exclusiv
Un element ce nu l-am întâlnit până în acest moment în operaţiile booleene este SAU-exclusiv. Deşi funcţia SAU este echivalentă cu o adunare booleeană, funcţia ŞI cu înmulţirea iar funcţia NU cu complementarea, nu există un echivalent boolean pentru funcţia SAU-exclusiv. Acest lucru nu ne împiedică să avem un simbol pentru reprezentarea ei:
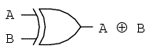
Acest simbol este folosit foarte rar în expresiile booleene, deoarece identitătile, proprietăţile şi regulile de simplificare ce implică adunare, înmulţire şi complementare nu se aplică şi acestei expresii. Totuşi, există o modalitate de reprezentare a funcţiei SAU-exclusiv cu ajutorul funcţiilor SAU şi ŞI:
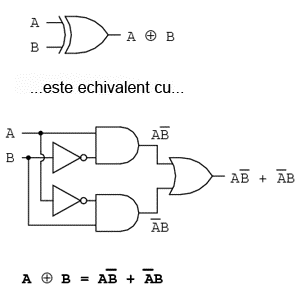
Ca şi echivalenţă booleeană. această regulă poate fi folositoare în cazul simplificării anumitor expresii booleene. Orice expresie de forma AB' + A'B (două porţi ŞI şi o poartă SAU), poate fi înlocuită de o singură poartă SAU-exclusiv.
7.8 Teoremele lui DeMorgan
DeMorgan a dezvoltat o serie de reguli importante în algebra liniară cu privire la complementul de grup. Prin complementul de grup ne referim la complenentul unui grup de termeni, şi nu doar la o singură variabilă.
Ţineţi minte de la capitolul legat de porţi logice, că inversând toate intrările unei porţi, inversăm şi fucţia logică esenţială a acesteia. O poartă SAU cu toate intrările inversate (o poartă SAU-negativă) se comportă precum o poartă ŞI-negat. O poartă ŞI cu toate intrările inversate (o poartă ŞI-negativă) se comportă precum o poartă SAU-negat. Teoremele lui DeMorgan exprimă aceiaşi echivalenţă în sens invers: inversând ieşirea unei porţi, funcţia rezultată este aceiaşi cu tipul opus de poartă cu intrările inversate:
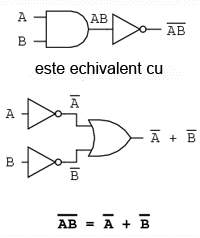
O bară deasupra termenului AB se comportă precum un simbol de grup. Acest lucru este total diferit faţă de produsul AB inversat separat (A'B'). Cu alte cuvinte, (AB)' nu este egal cu A'B'. Acest lucru are un impact profund asupra modului de evaluare şi de reducere a expresiilor booleene, după cum vom vedea.
Teorema lui DeMorgan poate fi gândită ca şi „întreruperea” complementului (bara orizontală). Atunci când simbolul complementului este rupt în doua, operaţia de sub el se modifică din adunare în înmulţirea şi invers. După aplicarea teoremei, fiecare variabilă are propriul ei complement. Ca şi exemplu:
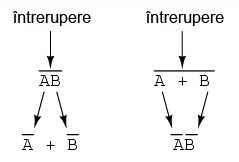
Când există mai multe complemente deasupra aceleiaşi expresii, nu putem întrerupe decât un complement pe rând. Cel mai uşor este să începem cu cea mai lungă linie orizontală (cea de sus). Ca şi exemplu, să considerăm expresia (A + (BC)')' redusă cu ajutorul teoremelor lui DeMorgan:
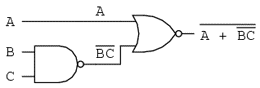
Urmând consideraţiile exprimate mai sus, aplicăm următorii paşi:

Ca şi rezultat, circuitul original este redus la un circuit format dintr-o poartă ŞI cu trei intrări, unde intrarea A este inversată printr-o poartă NU:
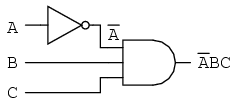
Ca şi contra-exemplu, nu întrerupeţi niciodată mai mult de un complement la un singur pas:
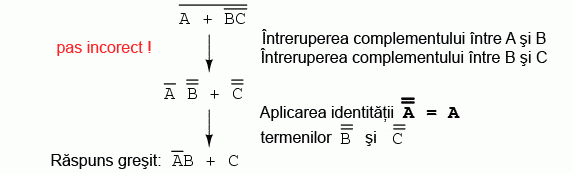
Pe cât de tentant pare, pe atât de incorect este să scurtăm paşi simplificării prin întreruperea mai multor complemente deodată. Prin urmare, nu faceţi niciodată acest lucru!
Putem simplifica expresia de mai sus şi prin întreruperea complementului scurt în primă instanţă, şi apoi a complementului lung:
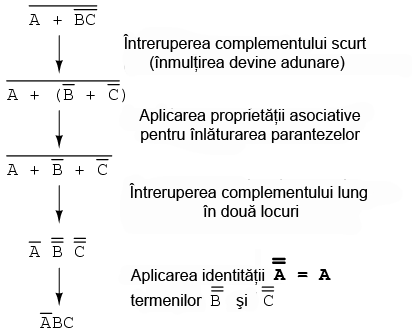
Desigur, rezultatul final este acelaşi şi în acest caz. Paşii necesari pentru simplificare sunt însă mai numeroşi faţa de exemplul precedent (întreruperea complementului lung la primul pas). La pasul al treilea, în exemplul de mai sus, întreruperea complementului lung se realizează în două locuri simultat. Această operaţie matematică este permisă, şi nu este identică cu întreruperea a două complemente deodată! Interidicţia întreruperii mai multor complemente deodată nu interzice întreruperea complementului în mai multe locuri.
Poate vă întrebaţi de ce am folosit paranteze în jurul sub-expresiei B'C din moment ce oricum le-am îndepărtat la pasul următor. Am făcut acest lucru pentru a sublinia un aspect important dar neglijat al teoremei lui DeMorgan. Din moment ce o linie orizontală lungă funcţionează ca şi simbol de grup, variabilele incluse sub aceasta trebuie să rămână grupate. În caz contrar, ordinea operaţiilor se pierde. În exemplul anterior, nu contează dacă am fi pus sau nu aceste paranteze, dar în alte cazuri s-ar putea să conteze. Să luăm un alt exemplu, meţinând parantezele:
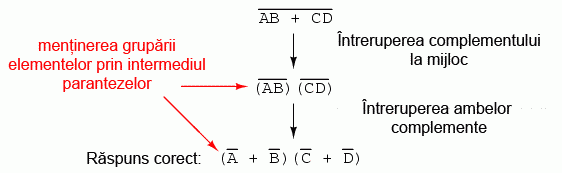
În cazul în care nu menţinem parantezele, riscăm să obţinem un răspuns greşit:
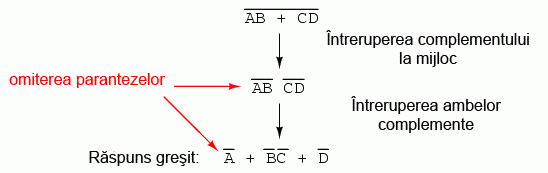
După cum se poate observa, menţinerea grupării realizate implicit prin liniile de complementare, este cruciale pentru obţinerea răspunsului corect.
7.8.1 Simplificarea unui circuit logic - exemplu
Să aplicăm acum principiile teoremelor lui DeMorgan pentru simplificarea unui circuit cu porţi logice:
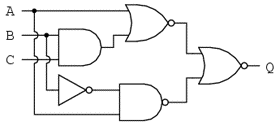
Expresia booleeană echivalentă
Ca de obicei, primul pas al simplificării circuitului constă în găsirea expresiei booleene echivalente. Putem face acest lucru prin notarea sub-expresiilor la ieşirea fiecărei porţi, pe măsură ce intrările ne sunt cunoscute:
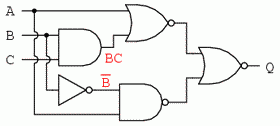
Apoi, notăm ieşirea primei porţi SAU-negat şi ieşirea porţii ŞI-negat. Atunci când aveam de a face cu porţi inversate pe ieşire, este mai uşor să scriem prima dată expresia fără inversarea finală. Observaţi şi de pe figură faptul că săgeata indică ieşirea porţii chiar înaintea inversării (cerculeţul de la ieşire). Expresia finală, după inversare, este complementul expresiei precedente. Astfel, ne putem asigura că nu uităm introducerea complementului în cadrul expresiei:
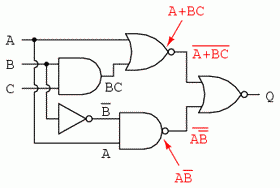
Şi, în sfârşit, ultimul pas constă în scrierea expresiei pentru poarta SAU-negat finală:
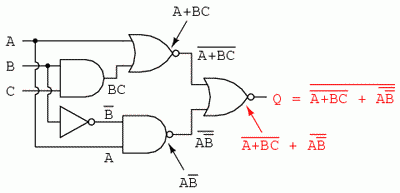
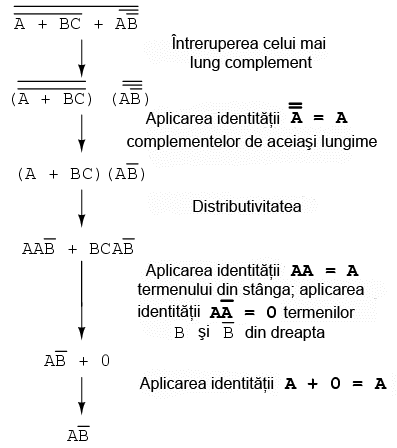
Simplificare expresiei echivalente
Trecem apoi la reducerea acestei expresii folosind identităţile, proprietăţile, regulile si teoremele (lui DeMorgan) algebrei booleene:
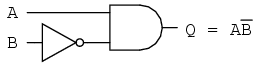
Circuitul echivalent
Circuitul echivalent al expresiei mult simplificate:
7.9 Transformarea tabelelor de adevăr în expresii booleene
Procesul de proiectare al circuitelor digitale începe adesea cu un tabel de adevăr. Acest tabel descrie modul de funcţionare al circuitului, pe scurt, ce funcţii trebuie aceasta să îndeplinească. Partea de proiectare constă în mare parte în determinarea tipului de circuit ce va realiza funcţia propusă în acest tabel de adevăr. Deşii există unii oameni care pot determina circuitul final prin simpla privire a tabelului de adevăr, pentru noi ceilalţi există o serie metode foarte utile. Se va dovedi că algebra booleeană este de un real folos în această situaţie.
Pentru ilustrarea acestor metode, cel mai indicat este să începem cu o problemă de proiectare practică. Să presupunem că trebuie să proiectăm un circuit de detectare a flăcării unui incinerator de deşeuri toxice. Astfel de tehnici de ardere sunt folosite de obicei pentru neutralizarea deşeurilor medicale, ce pot fi infectate cu viruşi sau bacterii periculoase:
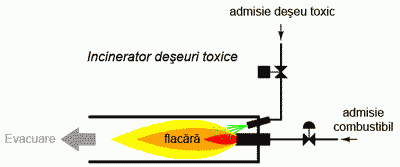
Atâta timp cât flacăra este menţinută în incinerator, injectarea deşeurilor toxice pentru neutralizare este sigură. Dacă în schimb flacăra se stinge, această alimentare a incineratorului se poate dovedi periculoasă. Evacuarea va conţine deşurile toxime ne-neutralizate, reprezentând un pericol de sănătate pentru persoanele aflate în apropiere. Avem nevoie prin urmare de un sistem de detectare a prezenţei flăcării. Injectarea deşeurilor va fi permisă doar atunci când sistemul de detectare ne asigură de prezenţa flăcării.
Există mai multe metode de detectare a flăcării: optic (detectarea luminii), termic (detectarea temperaturii înalte) şi conducţie electrică (detectarea particulelor ionizate). Fiecare din aceste metode prezintă avantaje şi dezavantaje. Să presupunem că, datorită pericolului ridicat al trecerii deşeurilor intacte prin evacuarea sistemului, s-a decis ca sistemul de detectare să fie redundant (senzori multiplii). Astfel că, defectare unuia dintre senzori să nu ducă la o situaţie nedorită. Fiecare senzor este echipat cu un contact normal-deschis (deschis - lipsă flacăra, închis - flacără detectată) necesar activării intrărilor unui sistem logic:
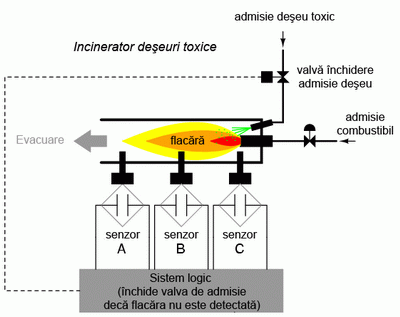
Scopul nostru acum, este să proiectăm circuitul logic astfel încât acesta să deschidă valva de admisie doar dacă există flacără (detectată de senzori). Prima dată trebuie să vedem comportamentul acestui sistem de control. Dorim ca valva să se deschidă în cazul în care doar unul din cei trei senzori detectează flacăra? Probabil că nu. Altfel, nu ar mai avea niciun rost să folosim trei senzori în loc de unul singur. Ceea ce ne dorim de la sistemul logic, este ca acesta să deschidă valva de admisie doar în cazul în care toţi cei trei senzori detectează flacăra. În acest caz, tabelul de adevăr arată astfel:
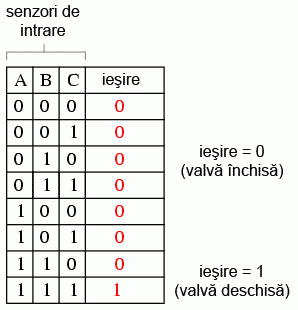
Această funcţionalitate poate fi asigurată folosind o poartă ŞI cu trei intrări: ieşirea circuitului este 1 doar dacă intrarea A ŞI intrarea B ŞI intrarea C este 1:
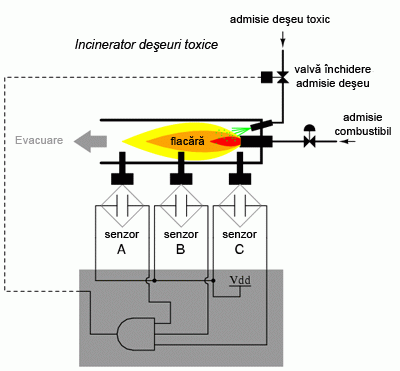
Dacă folosim în schimb relee electromecanice, putem crea această funcţie ŞI prin conectarea celor trei contacte în serie. Sau pur şi simplu conectă cei trei senzori în serie, astfel încât, singura modalitate prin care se poate deschide valva de admisie, este dacă toţi cei trei senzori indică prezenţa flăcării:
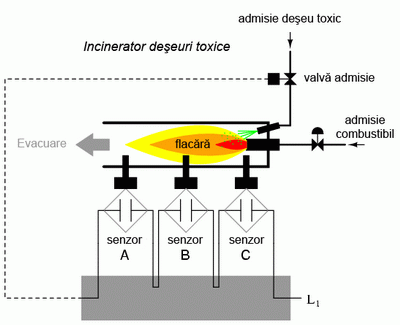
Deşi această strategie maximizează siguranţa sistemului, este totuşi foarte sensibilă la defect. În cazul în care unul din cei trei senzori se defectează, indicând lipsa flăcării din incinerator, întregul sistem se va opri. Asta chiar dacă ceilalţi doi senzori funcţionează şi indică prezenţa flăcării. Această oprire „gratuită” a incineratorului duce la pierderi de producţie şi de combustibil (menţinerea unei flăcări ce nu este folosită pentru incinerarea materialului toxic).
Va trebui să reproiectăm sistemul, astfel încât, un astfel de defect să nu ducă la închiderea întregului sistem. Bazându-ne pe doi senzori în detectarea prezenţei flăcării, sistemul îşi păstrează şi în acest caz redundanţa. O astfel de strategie implică un circuit logic cu trei intrări, a cărui ieşire este 1 în cazul în care cel puţin două din cele trei intrări sunt 1. Tabelul de adevăr arată astfel:
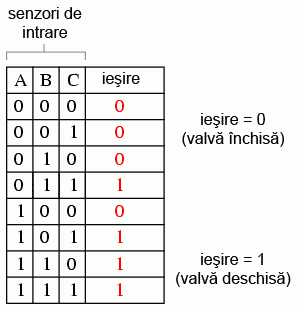
7.9.1 Suma-de-produse
În această situaţie nu este foarte clar ce tip de circuit logic ar satisface tabelul de adevăr. O metodă simplă de realizarea a unui astfel de circuit constă în utilizarea unei forme booleene standard, denumită sumă-de-produse. Ca şi exemplu, o astfel de expresie ar putea arătă astfel: ABC + BC + DF, suma produselor ABC, BC şi DF.
Astfel de expresii sunt relativ uşor de realizat cu ajutorul tabelelor de adevăr. Trebuie doar să găsim acele rânduri din tabel unde ieşirea este 1, şi să scriem apoi un produs boolean a cărui rezultat să fie 1, cunoscând condiţiile de intrare. De exemplu, să luăm al patrulea rând din tabelul de adevăr de mai sus. Ieşirea acestuia este 1 (ceea ce căutăm), iar intrările sunt A = 0, B = 1 şi C = 1. Produsul acestor trei variabile este unu dacă expresia arată astfel: A'BC.
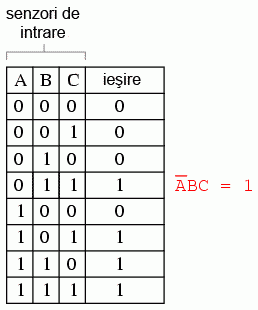
Să completăm şi celelalte rânduri care au o ieşire de 1, cu produsul termenilor:
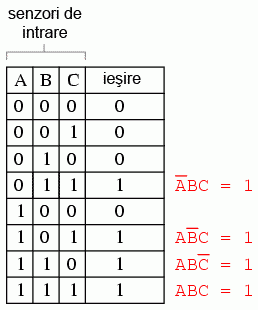
Însumăm toate aceste patru expresii, pentru a crea o singură expresie booleeană ce descrie în întregime tabelul de adevăr:
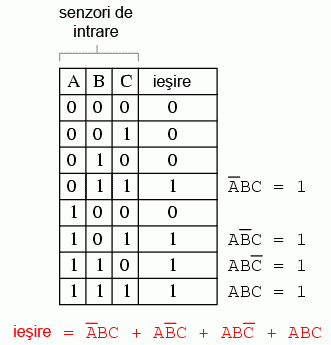
7.9.2 Realizarea circuitului logic
După ce am obţinut expresia booleeană sub formă de sumă-de-produse, putem trece la realizarea circuitului logic bazat pe această expresie, fie cu porţi logice:
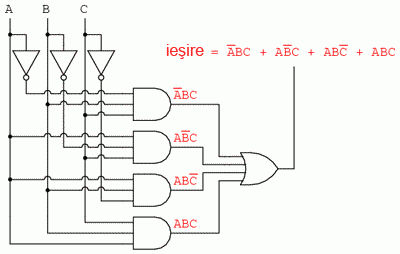
Fie cu relee electromecanice:
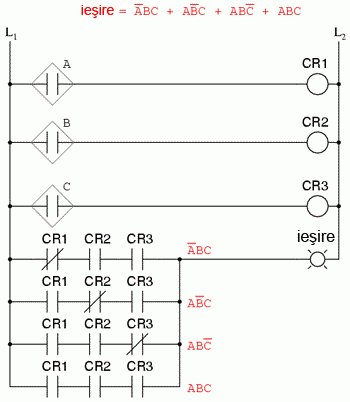 (relee electromecanice
(relee electromecanice
7.9.3 Simplificarea expresiei booleene
Din păcate, ambele variante sunt destul de complexe. Din fericire însă, putem simplifica expresia iniţială folosing regulile simplificării booleene:

Ca şi rezultat al simplificării, putem acum construi un circuit logic mult simplificat, dar care îndeplineşte exact aceiaşi funcţie logică, fie cu porţi logice:
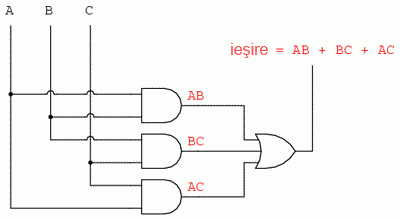
Fie cu relee electromecanice: