< Electronică Digitală

9 Circuite logice combinationale

9.1 Circuite logice combinaţionale - introducere

Termenul „combinaţional” provine din matematică. În matematică, o combinaţie reprezintă o mulţime neordonata. Pe scurt, este un mod de a spune că nimănui nu-i pasă ordinea elementelor mulţimii respective. Majoritatea jocurilor funcţionează exact în acest fel: dacă aruncăm zarurile, pe rând, nu contează dacă am dat un 2 urmat de 3 sau un 3 urmat de 2; rezultatul este acelaşi. Acelaşi lucru este valabil şi pentru circuitele lorgice combinaţionale: ieşirea circuitului este identică indiferent de ordinea intrărilor.

Desigur, există şi circuite a căror ieşire depinde de ordinea intrărilor, iar aceste circuite poartă numele de circuite logice secvenţiale. Deşi nu există un capitol cu acest titlul, următoarele capitole din volumul electronicii digitale se vor ocupa cu aceste circuite secvenţiale.

Circuitele practice sunt realizate dintr-o combinaţie de circuite logice combinaţionale şi secvenţiale. Cele secvenţiale asigură faptul că totul se întâmplă într-o anumita ordine. Cele combinaţionale realizează funcţii artimetice, logice sau de conversie.

Am folosit deja circuite logice combinaţionale. Fiecare dintre porţiloe logice discute este un astfel de circuit. Să urmărim comportamentul a două porţi logice ŞI-negat, atunci când intrările acestora sunt alimentate în diferite combinaţii.

Când ambele intrări sunt 0:

Când una dintre intrări este 1:

Când şi cealaltă intrare este 1:

Prin urmare, porţile ŞI-negat sunt indiferente la ordinea de alimentare a intrărilor. Acelaşi lucru este valabil şi pentru celelalte porţi logice discutate până în acest moment (ŞI, SAU-exclusiv, SAU, SAU-negat, SAU-negat-exclusiv şi NU).

9.2 Half-Adder

Ca şi prim exemplu a unui circuit logic combinaţional util, să realizăm un dispozitiv ce realizează adunarea a două numere binare. Putem calcula rapid care ar trebui să fie răspunsul unui astfel de dispozitiv:

0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 102        

Avem nevoie prin urmare de două intrări (a şi b) şi de două ieşiri. Prima ieşire o denumim Σ, deoarece reprezintă suma. A doua ieşire o numim C_out şi reprezintă bitul de depăşire. Tabelul de adevăr corespunzător este reprezentat mai jos:

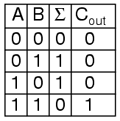
Simplificând ecuaţiile booleene, sau realizând o hartă Karnaugh, vom obţine circuitul de mai jos:

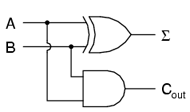
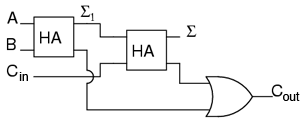
Dar să ne uităm mai atent la rezultate. Coloana Σ nu este altceva decât o poartă logică SAU-exclusiv. Coloana C_out reprezintă o poartă logică ŞI. Acest dispozitiv poartă numele de half-adder (semisumator), din motive pe care le vom vedea în secţiunea următoare.

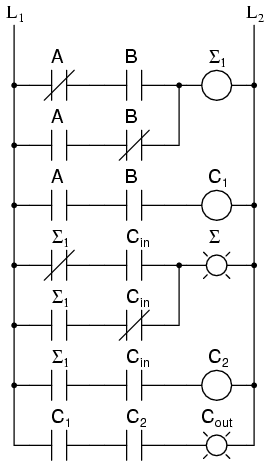
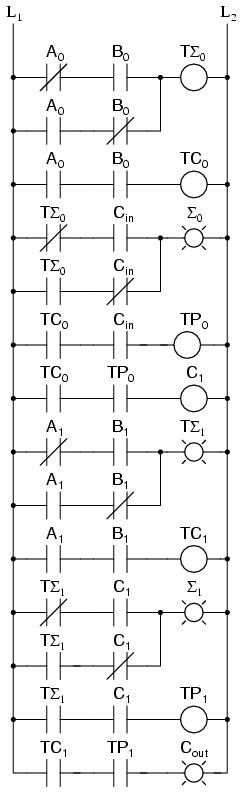
Sub forma unei diagrame ladder, circuitul de mai sus arată astfel:

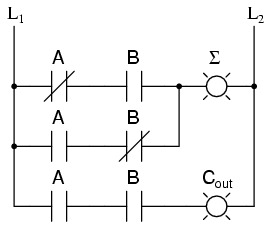
9.3 Full-Adder

Circuitul half-adder (semi-sumator) este extrem de util până în momentul în care dorim adăugarea unor valori ce nu pot fi reprezentate cu un singur bit. Cea mai lentă metodă de realizare a sumatoarelor pe doi biţi constă în realizarea unui tabel de adevăr (şi reducerea acestuia). Dacă avem nevoie de un sumator pe trei biţi, patru biţi, etc., repetăm acest proces. Circuitele vor fi rapide, dar timpul de realizare al lor va fi destul de lung.

Să ne uităm puţin la o sumă dintre două numere pe doi biţi. Putem să ne facem astfel o idee a circuitului ce dorim să-l implementăm:

11
 11
 11
---
110     

Putem observa numărul de intrări necesar coloanei din mijloc. Circuitul nostru sumator are nevoie de trei intrări: a, b şi bit-ul de depăşire. Putem folosi sumatorul cu două intrări pentru construirea unui sumator cu trei intrări.

Termenul Σ este destul de uşor de obţinut. Aritmetica ne spune că în cazul în care Σ = a + b + Cin şi Σ1 = a + b, atunci Σ = Σ1 + Cin:

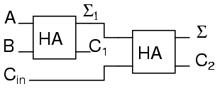
La ce ne ajută însă C₁ şi C₂? Să analizăm rezultatul adunării celor trei intrări:

Cin + a + b = ?
0 + 0 + 0 = 0     0 + 0 + 1 =  1     0 + 1 + 0 =  1     0 + 1 + 1 = 10
1 + 0 + 0 = 1     1 + 0 + 1 = 10     1 + 1 + 0 = 10     1 + 1 + 1 = 11
            

Dacă aveţi nelămuriri legate de bitul de rang inferior, puteţi verifica dacă circuitul şi diagrama ladder l-au calculat corect.

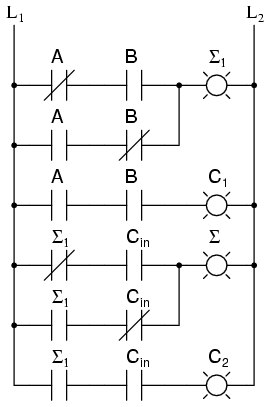
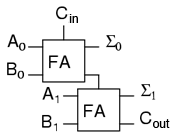
Pentru a calcula bitul de rang superior, putem observa că valoarea acestuia este 1 în ambele cazuri în care a + b produce un C₁. De asemenea, bitul de rang superior este 1 când a + b produce un Σ₁, iar C_in este 1. Prin urmare, vom avea un bit de depăşire ori de câte ori avem C₁ sau (Σ₁ şi C_in). Sumatorul nostru complet (full-adder) cu trei intrări, arată astfel:

Pentru unele circuite, eliminarea uneia sau mai multor tipuri de porţi poate fi importantă. Putem înlocui poarta SAU finală cu o poartă SAU-exclusiv fără a modifica rezultatele. Putem acum conecta două sumatoare pentru realizarea adunării numerelor pe 2 biţi:

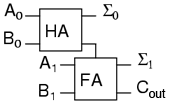
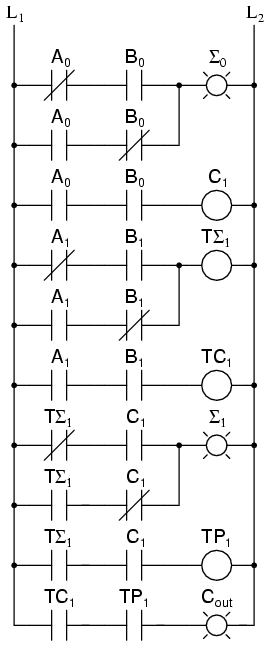
A₀ este bitul de rang inferior a lui A iar A₁ este bitul de rang superior a lui A. Acelaşi lucru este valabil şi pentru B. Σ₀ este bitul de rang inferior al sumei iar Σ₁ este bitul de rang superior al sumeri. C_out este bitul de depăşire.

9.3.1 Sume de numere mai mari de doi biţi

Un sumator pe doi biţi nu va fi realizat niciodată în acest fel. În schimb, biţi de rang inferior vor trece şi ei printr-un sumator complet (full-adder):

Există câteva motive pentru această alegere. Unul dintre ele este că în acest caz, permitem circuitului să determine dacă bitul de depăşire de rang inferior este inclus în sumă. Acest lucru permite însumarea unor numere mai mari.

Să considerăm două moduri diferite de analiză a unei sume de numere pe patru biţi:

111            1<-+  11<+-
 0110             |  01  |  10
 1011             |  10  |  11
-----          -  | —   | ---
10001          1  +-100  +-101
            

Dacă permitem programului însumarea numerelor pe doi biţi, şi reţinem bitul de depăşire, putem folosi acest bit de depăşire în următoarea sumă. În acest fel, programul poate însuma orice număr de biţi, chiar dacă folosim un sumator pe doi biţi.

9.3.2 Conectarea sumatoarelor între ele

Aceste sumatoare complete pot fi extinse pe un număr de biţi oricât de mare. Ca şi exemplu, un sumator pe 8 biţi poate fi realizat astfel:

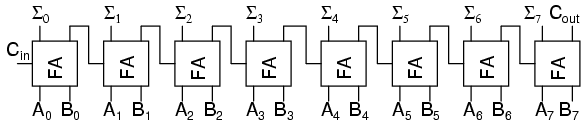
Acest rezultat este identic utilizării sumatoarelor pe doi biţi pentru realizarea unui sumator pe 4 biţi, şi utilizării a două astfel de sumatoare pe 4 biţi pentru realizarea unui sumator pe 8 biţi:

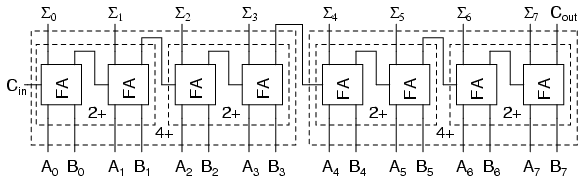
Fiecare „2+” este un sumator pe 2 biţi şi realizat din două sumatoare complete (full-adder). Fiecare „4+” este un sumator pe 4 biţi realizat din două sumatoare pe 2 biţi. Iar rezultatul celor două sumatoare pe 4 biţi este un sumator pe 8 biţi.

9..3 Multiplicarea circuitelor simple sau construirea integrală a dispozitivului

Există două metode principale de realizare a oricărui circuit logic combinaţional mare: putem folosi circuite simple, multiplicându-le; sau putem proiecta întregul circuit complex ca şi un singur dispozitiv. Utilizând circuite simple pentru realizarea circuitelor complexe, timpul petrecut pentru proiectarea lor scade foarte mult. Dezavantajul este că semnalele necesită un timp mai lung de propagare prin tranzistori. Sumatorul pe 8 biţi de mai sus trebuie să aştepte ca toate semnalele Cxout să treacă de la A0 + B0 spre intrările A7 + B7.

Dacă în schimb, proiectăm sumatorul pe 8 biţi ca şi dispozitiv complet, simplificat la o sumă de produse, atunci fiecare semnal trece printr-o singură poartă logică NU, o poartă logică ŞI şi o poartă logică SAU. Un dispozitiv cu 17 intrări are un tabel de adevăr cu 131.072 de intrări, iar reducerea acestor intrări la o sumă de produse va lua ceva timp.

Atunci când proiectăm circuite pentru sisteme ce au un timp de răspuns maxim pentru obţinerea rezultatului final, putem începe partea de proiectare prin utilizarea circuitelor sdimple. Putem încerca apoi înlocuirea porţiunilor de circuit ce sunt prea „lente”. În acest fel, ne putem concentra pe porţiunile de circuit care contează cel mai mult.