< Electronică Digitală
3 Porti logice
3.1 Semnale digitale şi porţi
Deşi sistemul de numeraţie binar reprezintă un concept matematic abstract interesant, încă nu am spus nimic despre aplicaţiile practice în electronică. Acest capitol este dedicat prin urmare aplicării conceptelor binare circuitelor electronice. Importanţa sistemului binar de numeraţie în electronica digitală este importantă datorită uşurinţei cu care putem reprezenta biţii sub formă fizică. Deoarece un bit poate avea doar două stăi diferite, fie 0 fie 1, orice mediu fizic ce poate funcţiona în două stări saturate diferite, poate fi folosit pentru reprezentarea unui bit. În consecinţă, orice sistem fizic ce este capabil să reprezinte biţi sub formă binară, poate reprezenta de asemenea şi valori numerice. Prin urmare, are potenţialul de a manipula aceste numere. Acesta este principiul de bază al circuitelor digitale.
Circuitele electronice sunt perfecte pentru reprezentarea numerelor binare. Tranzistorii, atunci când funcţionează la limită, se pot afla într-un din cele două stări: fie în stare blocată (curent de control zero), fie în stare de saturaţie (curent de control maxim). Dacă un circuit cu tranzistor este proiectat pentru maximizarea probabilităţii de funcţionare într-una din cele două stări (evitarea funcţionării tranzistorului în zona activă de funcţionare), acesta poate fi folosit ca şi reprezentare fizică a unui bit. Căderea de tensiune măsurată la ieşirea unui astfel de circuit poate fi folosită pentru reprezentarea unui singur bit. O tensiune joasă reprezentând „0”, şi o tensiune (relativ) înaltă reprezentând „1”.
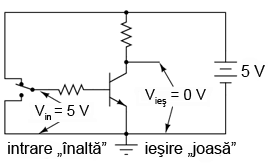
În figura alăturată, tranzistorul este saturat datorită tensiunii de intrare de 5 V (prin intermediul comutatorului cu două poziţii). Deoarece este saturat, căderea de tensiune dintre colector şi emitor este foarte mică, rezultând o tensiune de ieşire de practic 0 V. Dacă am folosit acest circuit pentru reprezentarea numerelor binare, am spune că semnalul de intrare este „1” binar, iar semnalul de ieşire este „0” binar. Orice tensiune apropiată de tensiunea de alimentare (având ca referinţă masa), este considerată a fi „1”, iar o lipsă de tensiune este considerată a fi „0”. Alternativ, se folosesc termenii de „înalt” (1 binar) sau jos (0 binar). Termenul general pentru reprezentarea unui bit prin intermediul unei tensiuni poartă numele de „nivel logic”.

Trecând comunatorul pe cealalţă poziţie, aplicăm o intrare de 0 binar si obţinem la ieşire 1 binar.
Ceea ce am creat mai sus poartă numele de poartă logică, sau simplu, poartă. O poartă nu este altceva decât un circuit amplificator special conceput pentru acceptarea şi generarea semnalelor de tensiune. Aceste semnale corespund numerelor binare 0 si 1. Prin urmare, porţile nu sunt concepute pentru amplificarea semnalelor analogice (semnale de tensiune între 0 şi tensiunea maximă). Mai multe porţi conectate împreună se pot folosi pentru stocare (circuite de memorare) sau manipulare (circuite de calcul). Ieşirea fiecărei porţi reprezintă în acest caz un singur bit dintr-un număr binar compus din mai mulţi biţi.
3.1.1 Poarta inversoare (NU sau NOT)
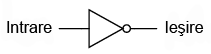
Alăturat este simbolul folosit pentru reprezentarea unei porţi inversoare (NOT). Aceasta se comportă identic cu circuitul analizat mai sus, şi anume: ieşirea porţii este inversă faţa de intrare (intrare 0, ieşire 1 sau intrare 1, ieşire 0). Aceste porţi sunt de fapt circuite cu tranzistoare de genul celui prezentat mai sus, dar, pentru simplificarea analizei circuitelor, se vor folosi aceste simboluri specifice fiecărei porţi.
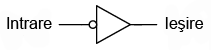
Un simbol alternativ pentru o poartă inversoare este cel din figura alăturată.
Forma triunghiulară este asemănătoare simbolului amplificatorului operaţional. După cum am spus mai sus, porţile sunt de fapt amplificatoare. Metoda standard de reprezentare a unei funcţii inversoare este prin intermediul acelui mic cerc desenat pe terminalul de intrare sau de ieşire. Dacă îndepărtăm acest cerc din simbolul porţii, lăsând doar triunghiul, acest simbol nu ar mai indica o inversare, ci o amplificare. Un astfel de simbol, şi o astfel de poartă chiar există, şi poartă numele de poarta ne-inversoare, sau buffer.
3.1.2 Poarta ne-inversoare (buffer)
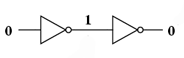
Dacă ar fi să conectăm două porţi inversoare, una în continuarea celeilalte, cele două funcţii de inversare s-ar „anula” reciproc. În acest caz, semnalul de ieşire va fi acelaşi cu cel de intrare.
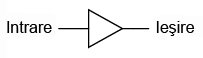
Pentru acest scop, există o poartă logică separată, denumită buffer (sau poartă ne-inversoare). Simbolul este un triunghiu simplu, precum în figura alăturată.
3.1.3 Reprezentarea conexiunilor
Asemănător simbolului amplificatorului operational, conexiunile de intrare şi de ieşire sunt reprezentate printr-un singur fir, punct de referinţă implicit pentru fiecare cădere de tensiune fiind masa. În circuitele logice, masa este aproape tot timpul reprezentată de către conexiunea negativă a sursei de alimentare. Sursele de alimentare duale sunt rareori folosite în astfel de circuite. Datorită faptului că circuitele logice (cu porţi) sunt de fapt nişte amplficatoare, acestea necesită o sursă de putere pentru funcţionare. La fel ca în cazul AO, conexiunile surselor de alimentare sunt omise pentru simplitate.
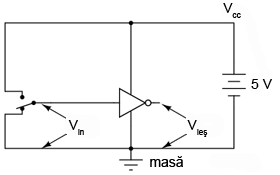
Dacă ar fi să reprezentăm toate conexiunile necesare pentru utilizarea acestei porţi, circuitul ar arăta precum cel din figura alăturată.
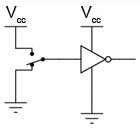
Conductorii surselor de alimentare sunt rareori reprezentaţi în circuitele electronice, chiar şi atunci când sunt reprezentate conexiunile pe fiecare poartă. Astfel, eliminând liniile ce nu sunt necesare, obţinem rezultatul alăturat.
Vcc reprezintă tensiunea constantă de alimentare a colectorului din circuitul cu tranzistor bipolar. Punctul de referintă este, desigur, masa. Punctele marcate cu Vcc sunt toate conectate la acelaşi punct, iar acel punct este borna pozitivă a sursei de alimentare de curent continuu. Valoarea acesteia este de obicei de 5 V.
3.1.4 Tabelul de adevăr
| Intrare | Ieşire |
|---|---|
| 0 | 1 |
| 1 | 0 |
O modalitate de exprimare a funcţiei unei porţi logice, poartă numele de tabel de adevăr. Aceste tabele descriu toate combinaţiile posibile ale intrărilor şi rezultatul ieşirilor. Pentru poarta inversoare, sau NOT, prezentată mai sus, tabelul de adevăr este cel alăturat.
| Intrare | Ieşire |
|---|---|
| 0 | 0 |
| 1 | 1 |
Pentru poarta ne-inversoare, tabelul de adevăr este puţin diferit.
Pentru porţi mai complexe, tabelele de adevăr sunt mai mari decât acesta. Numărul liniilor unui astfel de tabel trebuie să fie egal cu 2n, unde n reprezintă numărul intrărilor porţii logice considerate.
3.2 Porţi logice cu două intrări
Având doar o intrare, singurele porţi „disponibile” sunt cele inversoare şi cele ne-inversoare. Pentru a lucra cu mai multe posibilităţi, trebuie să mărim numărul de intrări.
O poartă cu o singură intrare prezintă doar două posibilităţi: fie intrarea este „înaltă” (1), fie este „joasă” (0). În schimb, o poartă cu doua intrări are patru posibilităţi (00, 01, 10, 11). O poartă cu trei intrări are opt combinaţii posibile (000, 001, 010, 011, 100, 101, 110 şi 111). După cum am mai spus, numărul combinaţiilor posible este egal cu 2n, unde n este numărul de intrări.
Datorită faptului că există aşa de multe posibilităţi folosind doar două terminale, există mai multe tipuri de porţi logice cu două intrări. Vom prezenta mai jos fiecare tip.
3.2.1 Poarta logică ŞI (AND)

Una dintre cele mai uşor de înţeles porţi este poarta ŞI. Denumirea vine de la faptul că ieşirea porţii va fi 1 dacă şi numai dacă toate intrările sunt 1. Asemenea, ieşirea va fi 0, dacă si numai dacă toate intrările sunt 0. Alăturat este prezentat simbolul porţii ŞI cu două, respectiv trei intrări.
| A | B | Ieşire |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Tabelul de adevăr pentru poarta ŞI cu două intrări este conform tabelului alăturat.
Practic, ceea ce se înţelege din tabelul de adevăr de mai sus poate fi ilustrat în cele ce urmează. Poarta logică ŞI este supusă tuturor posibilităţilor de intrare. Pentru determinarea nivelului logic de ieşire, se foloseşte un LED:
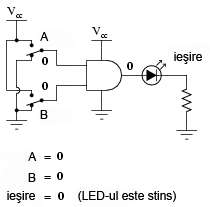
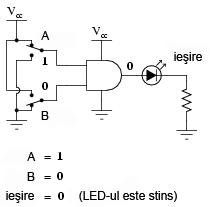
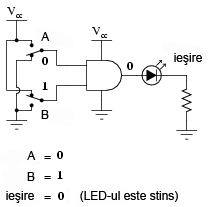
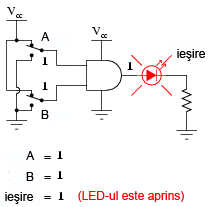
LED-ul este alimentat cu energie electrică doar atunci când ambele intrări logice sunt 1.
3.2.2 Poarta logică ŞI-negat (NAND)
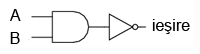
Poarta ŞI negat este o variaţie a porţii ŞI. Practic, comportamentul porţii este acelaşi ca al porţii ŞI, doar că la ieşire este conectată o poartă NU (inversoare).
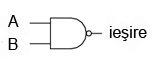
Pentru simbolizarea acestui lucru se trece un mic cerculeţ pe terminalul de ieşire.
| A | B | Ieşire |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Tabelul de adevăr este exact invers faţă de cel prezentat anterior pentru poarta ŞI.
După câte se poate observa, principiul este asemănător: ieşirea este 1 dacă toate intrările sunt 0 şi invers.
3.2.3 Poarta logică SAU (OR)
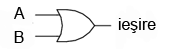
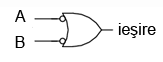
Ieşirea unei porţi logice SAU este 1 dacă oricare dintre intrări este 1. Ieşirea este 0 doar dacă toate intrările sunt 0.
| A | B | Ieşire |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Tabelul de adevăr este cel alăturat.
Următoarele ilustraţii redau modul de funcţionare a porţii SAU, atunci când cele două intrări foarmează toate combinaţiile posibile. Indicaţia vizuală a ieşirii este furnizată de un LED:
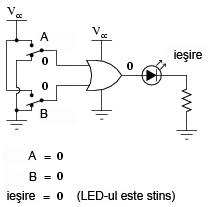
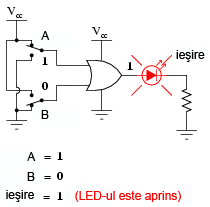
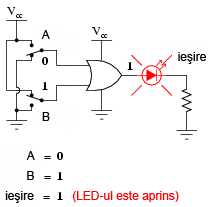
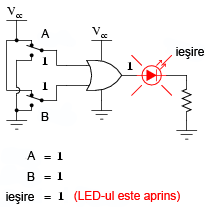
Dacă oricare dintre intrări se află în poziţia 1, LED-ul va fi alimentat cu energie electrică.
3.2.4 Poarta logică SAU negat (NOR)
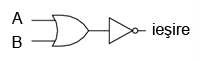
După cum probabil v-aţi dat seama, poarta SAU negată este o partă SAU cu valoarea de ieşire negată (0 negat este 1, iar 1 negat este 0). Schema echivalentă este cea din figura alăturată.
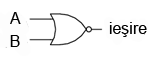
Pentru simplificarea reprezentării însă, există desigur un simbol special, conform figurii alăturate.
| A | B | Ieşire |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Tabelul de adevăr este exact invers faţă de cel al porţii SAU.
Principiul de bază este următorul: ieşirea este zero dacă cel puţin una dintre intrări este 1 şi este 1 doar atunci când ambele intrări sunt 0.
3.2.5 Poarta logică ŞI negativă
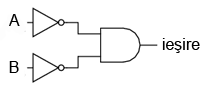
O poartă logică ŞI negativă funcţionează la fel ca o poartă ŞI având toate intrările inversate (conectate la porţi NU).
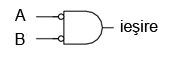
Conform standardului de notare, aceste intrări sunt simbolizate cu ajutorul unor cerculeţe.
| A | B | Ieşire |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Contrar intuiţiei, comportamentul logic al unei porţi ŞI negative nu este acelaşi cu al unei porţi ŞI negate. De fapt, tabelul său de adevăr este identic cu al unei porţi logic SAU negate.
3.2.6 Poarta logică SAU negativă
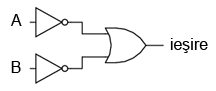
Conform aceluiaşi principiu, o poartă logică SAU negativă se comportă asemenea unei porţi SAU cu toate intrările inversate.
Conform standardului de notare, aceste intrări inversate sunt simbolizate prin cerculeţe.
| A | B | Ieşire |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Comportamentul logic şi tabelul de adevăr este exact acelaşi cu al unei porţi logice ŞI-negat.
3.2.7 Poarta logică SAU-exlusiv (XOR)
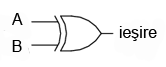
Ultimele şase variante de porţi logice au fost variaţii directe ale celor trei funcţii de bază: ŞI, SAU şi NU. Poarta SAU-exclusiv este însă diferită.
| A | B | Ieşire |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Ieşirea este 1 doar dacă intrările se alfă la nivele logice diferite, fie 0 şi 1, fie 1 şi 0. Altfel, ieşirea este 0 dacă toate intrările se află la acelaşi nivel logic.
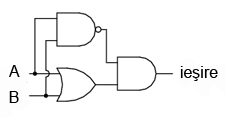
Circuitele echivalente pentru o poartă SAU-exclusiv sunt formate din porţi ŞI, SAU şi NU. O metodă directă de simularea a unei porţi SAU-exclusiv este prin introducerea în circuit pentru început a unei porţi SAU. Apoi adăugăm porţi astfel încât să impiedicăm o valoare de 1 pe ieşire atunci când ambele intrări sunt 1.
Putem verifica faptul că tabelul de adevăr al circuitului echivalent de mai sus este acelaşi cu tabelul de adevăr prezentat iniţial.
În acest circuit, poarta ŞI de ieşire se comportă ca un repetor (memorie) pentru poarta SAU atunci când ieşirea porţii ŞI-negat este 1. Acest lucru se întâmplă pentru primele trei combinaţii (00, 01 şi 10). Totuşi, atunci când ambele intrări sunt 1, ieşirea porţii SAU-negat este 0, forţând o valoare de 0 pe ieşirea porţii SAU.
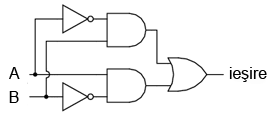
Un alt circuit echivalent pentru o poartă SAU-exclusiv este format din două porţi ŞI negate (cu ajutorul unei porţi NU). Acestea generează la ieşire o valoare de 1 dacă intrările sunt 01, respectiv 10. O poartă finală SAU permite o ieşire de 1 dacă cel puţin o poartă ŞI are o ieşire de 1.
Porţile SAU-exclusiv sunt utilizate în circuitele unde este necesară o comparaţie bit cu bine a două sau mai multe numere binare.
3.2.8 Poarta logică SAU-negat-exclusiv (XNOR)
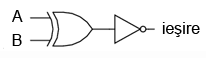
Ultima poartă pe care o vom analiza este poarta SAU-negat-exclusiv. Aceasta este echivalentă cu poarta SAU-exclusiv, doar că ieşirea este inversată.
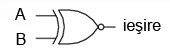
Desigur, şi pentru această poartă există un simbol special.
| A | B | Ieşire |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Şi, în sfârşit, să vedem cum arată tabelul de adevăr pentru această poartă.
Aşa cum reiese din acest tabel, scopul unei porţi logice SAU-negat-exclusiv este de a genera un nivel logic 1 atunci când ambele intrări sunt la acelaşi nivel (fie 00, fie 11).
3.3 Principiul universalităţii
Porţile logice ŞI-negat şi SAU-negat posedă o proprietate specială: sunt universale. Cu alte cuvinte, având un număr suficient de astfel de porţi, fiecare din ele poate simula modul de funcţionare al oricărei alte porţi. De exemplu, putem construi un circuit care să se comporte precum o poartă SAU, folosind trei porţi ŞI-negat interconectate. Această abilitate este caracteristică doar acestor două tipuri de porţi. Practic, multe sisteme de control digital sunt construite doar cu ajutorul porţilor ŞI-negat şi SAU-negat, toate funcţiile logice necesare fiind derivate prin interconectarea acestor tipuri de porţi.
Vom lua mai jos câteva astfel de exemple.
3.3.1 Realizarea funcţiei NU
Să revedem prima dată simbolul şi tabelul de adevăr pentru poarta NU:
| Intrare | Ieşire |
|---|---|
| 0 | 1 |
| 1 | 0 |

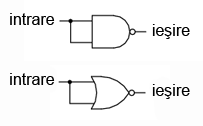
În figura alăturată este prezentat modul de realizare a acestei funcţii folosind porţi logice ŞI-negat şi SAU-negat.
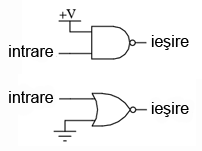
Această metodă de conectare împreună a intrărilor duce la creşterea curentului de intrare. Prin urmare, atât în cazul de faţă, cât şi în exemplele ce urmează, se va folosi conectarea la masă a unuia dintre terminali (celălalt terminal de intrare va fi legat la sursa de alimentare). Funcţional, rezultatul este acelaşi.
3.3.2 Realizarea funcţiei ne-inversoare (buffer)
Să revedem prima dată simbolul şi tabelul de adevăr pentru o poartă ne-inversoare:
| Intrare | Ieşire |
|---|---|
| 0 | 0 |
| 1 | 1 |

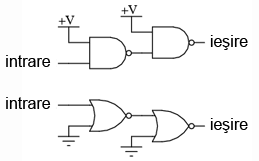
Conform celor spuse mai sus, realizarea acestei funcţii folosind porţi logice ŞI-negat şi SAU-negat se realizează conectând două etaje împreună, conform figurii alăturate.
3.3.3 Realizarea funcţiei ŞI
Simbolul şi tabelul de adevăr al porţii logice ŞI:
| A | B | Ieşire |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
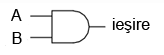
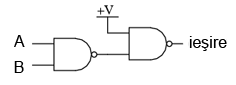
Folosind porţi logice ŞI-negat pentru realizarea funcţiei ŞI, avem nevoie de adăugarea unui etaj inversor (poartă NU) pe ieşirea porţii ŞI-negat. Dar, am văzut mai sus cum se poate realiza o poartă NU folosind o poartă ŞI-negat. Prin urmare, schema finală este cea din figura alăturată.
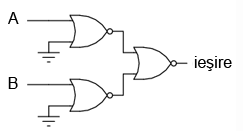
Acelaşi lucru se poate realiza folosind porţi logice SAU-negat, prin inversarea (poartă NU) tuturor intrărilor printr-o poartă SAU-negat. Din nou, am văzut mai sus cum se poate realiza o poartă NU dintr-o poartă SAU-negat.
3.3.4 Realizarea funcţiei ŞI-negat
| A | B | Ieşire |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |

Desigur, nu avem ce „construi” la o funcţie ŞI-negat cu ajutorul porţilor ŞI-negat, pentru că nu este nimic de făcut.
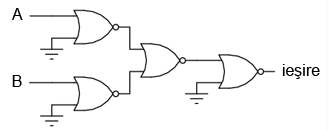
Cu ajutorul porţilor SAU-negat însă, va trebui să inversăm atât intrările cu o poartă SAU-negat, precum şi ieşirea acesteia din urmă (cu o poartă NU). Din nou, am văzut mai sus cum se poate realiza o poartă NU cu ajutorul porţii SAU-negat.
3.3.5 Realizarea funcţiei SAU
| A | B | Ieşire |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |

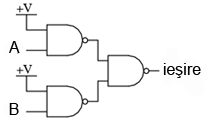
Inversarea ieşirii unei porţi SAU-negat (cu ajutorul unei alte porţi SAU-negat conectată ca şi poartă NU) are ca rezultat funcţia SAU.
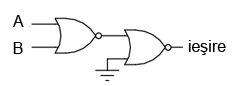
Folosind porţi SAU-negat, trebuie să inversăm toate intrările pentru simularea funcţiei SAU, la fel cum a trebui să inversăm toate intrările unei porţi SAU-negat pentru a obţine funcţie ŞI.
Ţineţi minte că inversarea tuturor intrărilor unei porţi rezultă în schimbarea funcţiei esenţiale ale acesteia. Astfel, poarta ŞI devine SAU, iar poarta SAU devine ŞI, plus o ieşire inversată. Astfel, cu toate intrările inversate, o poartă ŞI-negat se comportă precum o poartă SAU; o poartă SAU-negat se comportă precum o poartă ŞI; o poartă ŞI se comportă precum o poartă SAU-negat; şi, în fine, o poartă SAU se comportă precum o poartă ŞI-negat. În cadrul algebrei booleene, aceste transformări sunt cunoscute sub numele de „teorema lui DeMorgan”.
3.3.6 Realizarea funcţiei SAU-negat
| A | B | Ieşire |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |

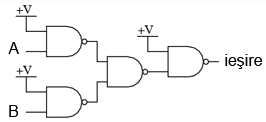
Pentru realizarea acestei fucţii folosind porţi ŞI-negat, trebuie să inversăm toate intrările şi ieşirea. Procedeul este asemănător cu cel prin care am realizat funcţia ŞI-negat folosind porţi logice SAU-negat.
3.4 Modul de împachetare
Circuitele digitale cu porţi logice sunt confecţionate ca şi circuite integrate: toţi tranzistori şi rezistorii ce intră în componenţa circuitului sunt construiţi pe o singură bucată de material semiconductor. Prin urmare, dacă avem nevoie de un număr relativ de porţi logice, putem folosi circuite integrate sub forma capsulelor DIP. Aceste circuite integrate sunt disponibile cu un număr par de pini, cele mai comune fiind cu 8, 14, 16, 18 sau 24 de pini
Numărul de catalog al acestor capsule indică numărul şi tipul porţilor conţinute în pachet. Aceste numere de catalog sunt standardizate, ceea ce înseamnă că un circuit „74LS02” produs de Motorola este indentic ca şi funcţionalitate cu un circuit „74LS02” produs de Fairchild sau de oricare alt producător. Codul de litere ce precedă aceste numere de catalog sunt însă unice fiecărui producător în parte. De exemplu „SN74LS02” reprezintă o capsulă cu patru porţi logice SAU-negat, produsă de Motorola. Un „DM74LS02” este acelaşi circuit din punct de vedere funcţional, dar produs de Fairchild.
Mai jos sunt date ca şi referinţă câteva capsule DIP dintre cele mai utilizate: