< Curent continuu

7 Circuite combinate

7.1 Ce este un circuit serie-paralel

În cazul circuitelor serie simple, toate componentele sunt legate cap la cap şi formează o singură cale pentru curgerea electronilor prin circuit:

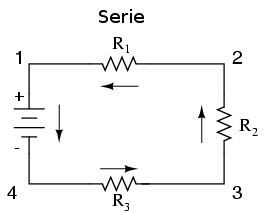
În cazul circuitelor parale simple, toate conponentele sunt legate legate între acelaşi set de puncte comune din punct de vedere electric, formându-se asfel mai multe căi pentru curgerea electronilor de la un capăt la celălalt al bateriei:

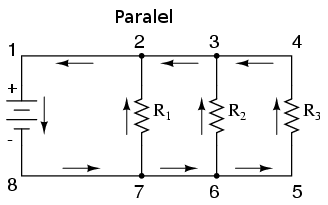
În ambele cazuri, avem de a face cu anumite seturi specifice de reguli pentru relaţiile dintre tesiune, curent şi rezistenţă. (notă: vezi circuitele serie şi circuitele paralel)

Dar, în cazul în care o parte dintre componente sunt legate în serie şi o altă parte a componentelor în paralel, nu este posibilă aplicarea unei singure reguli pentru întreg circuitul, sau pentru fiecare parte constituentă. În schimb, vom încerca identificarea părţilor serie din circuit şi a părţilor paralele, ca mai apoi să aplicăm regulile necesare în funcţie de tipul circuitului. Să vedem un exemplu:

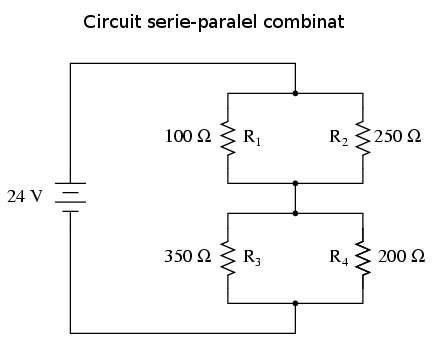
Acesta nu este nici un circuit serie simplu nici unul paralel simplu, ci conţine elementele din ambele tipuri. Curentul iese prin partea de jos a bateriei, se împarte (ramifică) pe cele două ramuri spre R₃ şi R₄, se re-întâlneşte, se ramifică încă odată spre R₁ şi R₂, se re-întânleşte din nou şi se re-întoarce la baterie. Există mai mult de un singur drum pentru circulaţia curentului (nu este serie), dar totuşi, există mai mult decât două seturi de puncte electric comune (nu este paralel).

Deoarece circuitul este o combinaţie între serie şi paralel, nu putem aplica relaţiile de tensiune, curent sau rezistenţă direct în tabel precum a fost cazul circuitelor serie şi paralel simple. De exemplu, dacă circuitul de mai sus ar fi fost serie simplu, am putea pur şi simplu să adunăm cele patru rezistenţe şi să obţinem rezistenţa finală, să calculăm apoi curentul total, şi apoi căderile de tensiune pe fiecare rezistor. Asemănător, dacă circuitul ar fi fost paralel simplu, am fi putut afla curenţii prin fiecare ramură, suma lor ne-ar fi dat curentul total iar de acolo puteam calcula rezistenţa totală. Totuşi, soluţia acestui circuit este puţin mai complexă de atât.

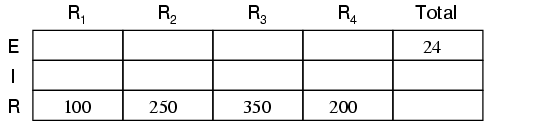
Tabelul este folositor pentru aflarea diferitelor valori într-un circuit serie-paralel, dar trebuie să fim atent cum şi unde aplicăm regulile pentru fiecare tip de circuit în parte (serie şi paralel).

Dacă putem distinge care părţi din circuit sunt serie şi care paralel, putem analiza circuitul în mai multe etape, fiecare etapă pe rând, folosind regulile corecte pentru determinarea relaţiilor dintre tensiune, curent şi rezistenţă. Restul capitolului va fi dedicat acestor tehnici.

7.2 Tehnici de analiză a circuitelor

Scopul analizei circuitului serie-paralel este determinarea tuturor căderilor de tensiune, curenţilor şi puterilor disipate în circuit. Strategia generală pentru atingerea acestui scop este următoarea:

1. Determinăm conexiunile existente din circuit: care rezistori sunt legaţi în serie şi care în paralel
2. Redesenăm circuitul, înlocuind fiecare din combinaţiile serie sau parelel din circuit identificate la primul punct, cu un singur rezistor echivalent. Dacă folosim un tabel pentru scrierea valorilor, atunci vom realiza o nouă coloană în tabel pentru fiecare rezistenţă echivalentă
3. Repetăm paşii 1 şi 2 până ce întreg circuitul este redus la un singur rezistor echivalent
4. Calculăm curentul total cunoscând tensiunea şi rezistenţa totală folosind legea lui Ohm (I=E/R)
5. Folosind valorile totale ale tensiunii şi ale curentului, mergem un pas înapoi, spre ultima reducere echivalentă din circuit şi inserăm valorile în locurile necesare
6. Cunoscând rezistenţele şi tensiunea totală / curentul total de la pasul 5, folosim legeal lui Ohm pentru calcularea valorilor necunoscute (tensiuni sau curenţi) (E=IR sau I=E/R)
7. Repetăm paşii 5 şi 6 până când toate valorile tensiunii şi ale curentului sunt cunoscute în configuraţia iniţială a circuitului. Practic, mergem pas cu pas de la versiunea simplificată a circuitului spre versiunea originală, complexă a acestuia, introducând valorile tensiunii şi ale curentului acolo unde este necesare până când toate valorile tensiunilor şi curenţilor sunt cunoscute
8. Calculăm puterile disipate în circuit din valorile cunoscute ale tensiunilor, curenţilor şi/sau rezistenţelor.

Deşi sună destul de complicat, vom înţelege întreg procesul mult mai uşor dacă luăm un exemplu practic:

În exemplul de mai sus, rezistorii R₁ şi R₂ sunt conectaţi în paralel; la fel şi R₃ cu R₄. Pentru că am identificat aceast tip de conecţiune ca fiind una paralelă, putem înlocui fiecare din cele două combinaţii printr-o singură rezistenţă echivalentă. Circuitul redesenat arată asfel:

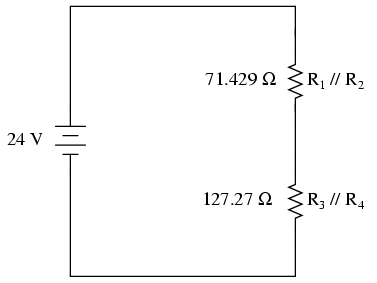
Simbolul (//) este folosit pentru a reprezentă faptul că valoarea celor două rezistoare a fost obţinută cu ajutorul formule 1/(1/R). Rezistorul de 71.429 Ω de sus este echivalentul celor doi rezistori R₁ şi R₂ legaţi în paralel. Rezistorul de 127.27 Ω de jos este echivalentul celor doi rezistori R₃ şi R₄ legaţi în paralel.

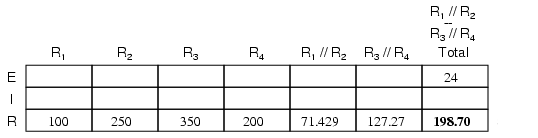
Tabelul valorilor poate fi mărit cu două coloane pentru a include şi valorile acestori doi rezistori echivalenţi:

Ar trebui să devină aparent că circuitul a fost redus la o configuraţie serie simplă ce conţine doar doi rezistori (echivalenţi). Pasul final în reducerea circuitului este adunarea acestor două rezistenţe şi aflarea rezistenţei totale a circuitului. Rezultatul acestei adunări este 198.70 Ω. Acum putem re-desena circuitul cu o singură rezistenţă echivalentă. Adăugăm, de asemenea, încă o coloană în tabel. Notaţia coloanei este (R₁//R₂–R₃//R₄) pentru a indica modul iniţial de conectare al rezistenţelor în circuit. Simbolul „–” reprezintă conexiune „serie”, iar simbolul „//” reprezintă conexiune „paralel”.

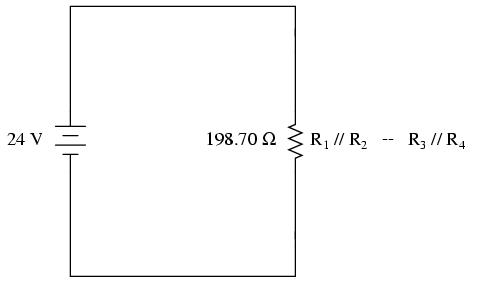
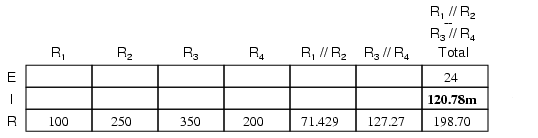
În acest moment putem folosi legea lui Ohm (I=E/R) pentru determinarea curentului total prin circuit şi completarea coloanei corespunzătoare din tabel:

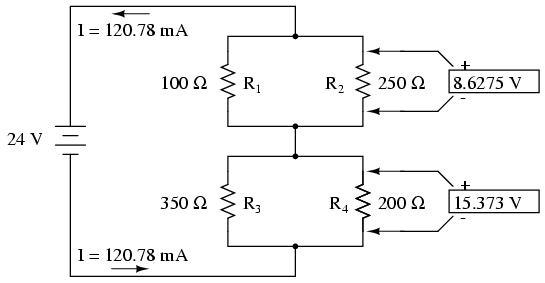
Reîntorcându-ne la diagrama circuitului, valoarea totală a curentului este momentan singura ce apare pe desen:

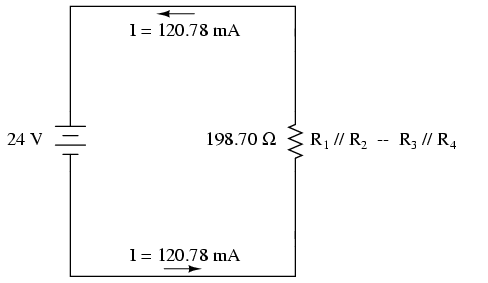
Acum putem începe să ne re-întoarcem la paşii anteriori în simplificarea circuitului spre configuraţia originală. Pasul următor este să ne întoarcem la circuitul în care R₁//R₂ şi R₃//R₄ sunt în serie:

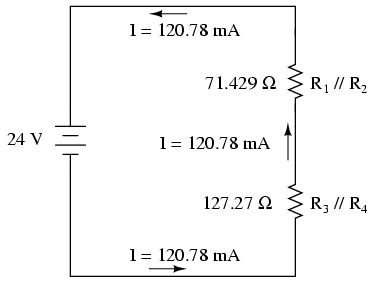
Din moment ce R₁//R₂ şi R₃//R₄ sunt în serie, curentul prin ambele seturi de rezistenţe echivalente este acelaşi. Mai mult decât atât, valoarea curentului prin ele trebuie să fie egală valorii curentului total; putem completa coloana curent total din tabel cu valoarea curentului total pentru fiecare din cele două grupuri de rezistenţe echivalente:

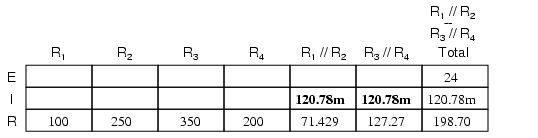
Cunoscând curentul prin rezistenţele echivalente R₁//R₂ şi R₃//R₄, putem aplica legea lui Ohm (E=IR) pentru aflarea căderilor de tensiune pentru fiecare grup în parte, completând şi tabelul:

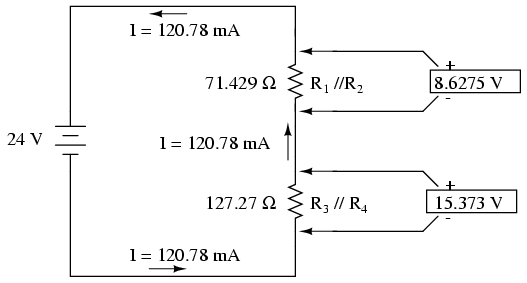
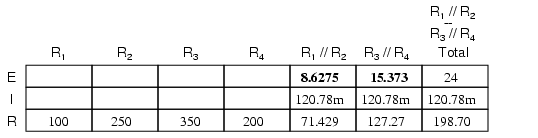
Deoarece ştim că R₁//R₂ şi R₃//R₄ sunt defapt conexiuni echivalente paralele, iar căderile de tensiune în circuitele paralele sunt egale. Cu alte cuvinte, putem să mai facem un pas înapoi spre configuraţia iniţială a circuitului şi să completăm tabelul cu valorile calculate:

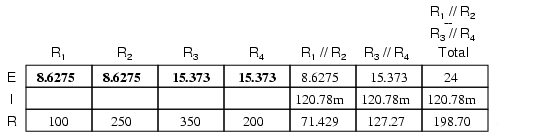
Secţiune originală a tabelului pentru rezistori este acum completată (coloana R₁ la R₄). Aplicând legea lui Ohm pentru celelalte valori rămase necompletate (I=E/R), putem determina valorile prin R₁, R₂, R₃ şi R₄:

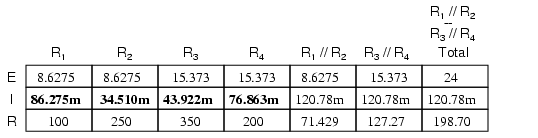
Circuitul iniţial cu toate valorile tensiunilor, curenţilor şi a rezistenţelor arată asfel:

mg src="../poze/00130.png" alt="00130.png" title="circuit electric"/>