Introducere in circuite electrice si electronice

< Electronică Digitală

8 Hărţi Karnaugh

8.1 De ce hărţi Karnaugh

La ce ne folosesc hărţile Karnaugh? Harta Karnaugh, asemenea algebrei booleene, este o metodă de simplificare a circuitelor logice digitale. Vedeţi exemplul „incineratorului de deşeuri toxice” ca şi exemplu de simplificare booleană a unui circuit logic. Harta Karnaugh va simplifica circuitul mult mai rapid şi mai uşor în majoritatea cazurile.

Simplificarea booleană este de fapt mai rapidă în cazul în care avem maxim două variabile booleene. Putem folosi această metodă chiar şi în situaţia în care avem trei variabile, dar metoda booleană este mai greoaie în acest caz. Cu patru variabile de intrare, algebra booleeană devine „imposibilă”. Hărţile Karnaugh sunt mai rapide şi mai uşor de implementat. Acestea pot fi folosite cu succes în situaţiile în care avem până la şase variabile de intrare. Între şase şi opt, mai putem încă folosi aceste hărţi. Peste această valoare, este indicat să folosim un program software specializat pentru realizarea simplificărilor logice.

8.2 Diagrame Venn

Matematicienii utilizează diagramele Venn pentru reprezentarea relaţiilor logice dintre mulţimi (colecţii de obiecte). Ne vom folosi de diagramele Venn pentru a face tranziţia dintre algebra booleană şi hărţile Karnaugh.

8.2.1 Mulţimi şi submulţimi

O mulţime este o colecţie de obiecte dintr-un univers dat. Elementele mulţimii sunt obiecte ce aparţin mulţimii. Elementele unei mulţimi au de obicei ceva în comun, deşi acest lucru nu este neapărat necesar. Din universul numerelor reale, de exemplu, mulţimea tuturor numerelor întregi pozitive {1, 2, 3 …}, este o mulţime. Mulţimea {3, 4, 5} este o mulţime mai mică, sau o submulţime a mulţimii numerelor întregi pozitive. Un alt exemplu este mulţimea tuturor băieţilor dintr-o clasă (reprezentând universul discuţiei). Vă puteţi gândi şi la alte mulţimi?

8.2.2 Diagrame Venn - exemple

Diagrama Venn din figura de mai jos stânga, reprezintă mulţimea A (în interiorul cercului) din universul U (aria dreptunghiulară). Dacă tot ceea ce se află în interiorul cercului este A, atunci tot ceea ce se află în exteriorul cercului nu este A (A-negat). Prin urmare, in figura de mai jos centru, denumit aria dreptunghiulară din afara cercului A cu A-negat în loc de U. B şi B-negat se reprezintă similar (figura de mai jos dreapta).

Ce se întâmplă dacă şi A şi B se află în acelaşi univers? Există patru posibilităţi:

Să reluăm fiecare din cele patru posibilităţi în parte:

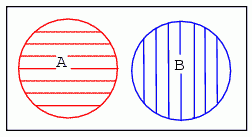
Primul exemplu indică faptul că mulţimile A şi B nu au niciun element comun, conform diagramei Venn. Regiunile celor două mulţimi nu se suprapun în niciun punc. De exemplu, să presupunem că mulţimile A şi B ar conţine următoarele elemente: A = {1, 2, 3, 4}, B = {5, 6, 7, 8}. Niciunul dintre elementele mulţimii A nu este inclus în mulţimea B şi invers. Prin urmare, cele două cercuri nu se suprapun.

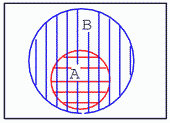
În cel de al doilea exemplu, mulţimea A este inclusă total în mulţimea B. Cum putem explica această situaţie? Să presupunem că mulţimile A şi B conţin următoarele elemente: A = {1, 2}, B = {1, 2, 3, 4, 5, 6, 7, 8}. Toate elementele din A se regăsesc şi în B. Prin urmare, mulţimea A este o submulţime a mulţimii B, iar cercul A este inclus în cercul B.

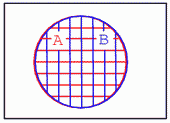
În cel de al treilea caz, mulţimile A şi B se suprapun perfect. Din diagrama Venn, putem deduce că cele două mulţimi conţin exact aceleaşi elemente. Să presupunem că mulţimile arată astfel: A = {1, 2, 3, 4} şi B = {1, 2, 3, 4}. Prin urmare A = B. Cele două mulţimi sunt identic egale deoarece conţin exact aceleaşi elemente.

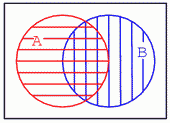
În ultimul caz, cele două mulţimi se suprapun, dar nu complet ci doar parţial. Acest lucru ne spune că există elemente comune celor două mulţimi, dar fiecare mulţime are si elemente unice. Să presupunem că cele două mulţimi ar arăta astfel: A = {1, 2, 3, 4} şi B = {3, 4, 5, 6}. Ambele mulţimi conţin elementele 3 şi 4. Acesta este şi motivul pentru care cele două cercuri sunt suprapuse.

8.3 Relaţii booleene cu diagrame Venn

8.3.1 Funcţia logică SAU (adunarea booleană)

În ultimul exemplu din secţiunea precedentă, mulţimile A şi B s-au suprapus parţial. Iniţial, ne vom concentra atenţia asupra întregii regiuni haşurate de mai jos, abia apoi vom trece la analizarea regiunii comune celor două mulţimi. Să utilizăm expresii booleene pentru desemnarea reginilor diagramelor Venn, conform figurii de mai jos:

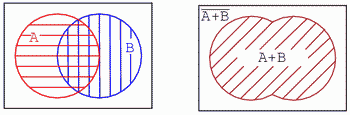
Aria mulţimii A este haşurată cu roşu, iar cea a mulţimii B cu albastru. Dacă analizăm întreaga aria haşurată (suma totală a tuturor ariilor haşurate), indiferent de culoare sau stil, obţinem figura din dreapta sus. Aceasta corespunde funcţiei logice SAU, iar expresia booleană este A + B, aria fiind cea haşurată cu linii diagonale. Tot ceea ce se află în afară ariei haşurate reprezintă (A + B)-negat.

8.3.2 Funcţia logică ŞI (înmulţirea booleană)

O altă metodă de interpretare a diagramei Venn cu regiuni suprapuse, este analizarea regiunii comune atât mulţimii A cât şi mulţimii B, aria dublu haşurată de mai jos (stânga). Această arie corespunde funcţiei logice ŞI, iar expresia booleană este AB (jos dreapta). Tot ceea ce se află în afara ariei dublu haşurate AB reprezintă AB-negat:

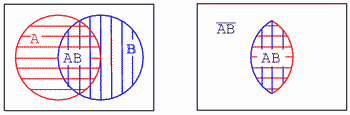
Observaţii că unele elemente ale mulţimilor A şi B de sus, sunt elemente ale mulţimii (AB)-negat, dar niciunul dintre elementele mulţimii (AB)-negat nu se află în interiorul ariei dublu haşurate AB.

8.3.3 Expresii booleene

Diagrama Venn pentru A'B

Vom trece acum la dezvoltarea unei expresii booleene. De exemplu, să presupunem că dorim reprezentarea prin diagrame Venn a expresiei booleene A'B (A-negat ŞI B).

Paşii sunt următorii: haşurarea ariei A' (A-negat); haşurarea ariei B; realizarea funcţiei ŞI (A'B) prin suprapunerea celor două regiuni precedente. Am putea să ne oprim aici, dar, pentru claritate, putem păstra doar aria dublu haşurată:

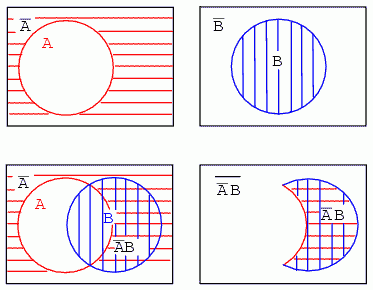
Expresia A'B reprezintă regiunea în care A' şi B se suprapun. Regiunea nehaşurată din afara ariei A'B este (A'B)'.

Diagrama Venn pentru B' + A

Putem încerca acelaşi lucru cu expresia booleană SAU. De exemplu, să presupunem că dorim să reprezentăm prin diagrame Venn expresia B' + A.

Paşii sunt următorii: începem cu haşurarea lui B, şi apoi a regiunii B'; suprapunem A peste B'. Din moment ce suntem interesaţi de realizarea funcţiei SAU, vom căuta să reprezentăm întreaga arie formată de cele două mulţimi, indiferent de stilul haşurării. Prin urmare A + B' reprezintă întreaga arie haşurată:

Pentru claritate, putem reprezenta întreaga regiune printr-o singură haşurare (jos stânga):

Diagrama Venn pentru (A + B')'

Aria haşurată cu verde de mai sus este rezultatul expresiei A + B'. Trecând la (A + B')', căutam complementul expresiei A + B', reprezentat prin aria nehaşurată din figura de mai sus stânga. Aplicând teorema lui DeMorgan şi negarea dublă (A'' = A), ajungem la rezultatul (A + B')' = AB'. Prin urmare, cele două regiuni sunt identice.

Putem face acum observaţia că diagramele Venn nu demonstrează nimic. Avem nevoie de algebra booleană pentru acest lucru. Totuşi, diagramele Venn pot fi utilizate pentru verificare şi vizualizare. În exemplul de mai sus, am verificat şi vizualizat teorema lui DeMorgan cu ajutorului unei diagrame Venn.

Diagrama Venn pentru A' + B' şi (A' + B')'

Arătaţi că A' + B' = AB

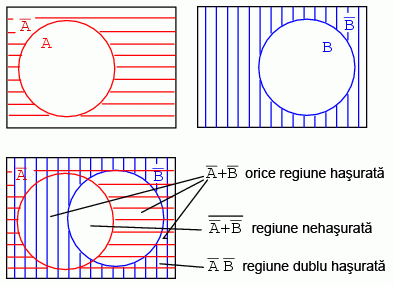
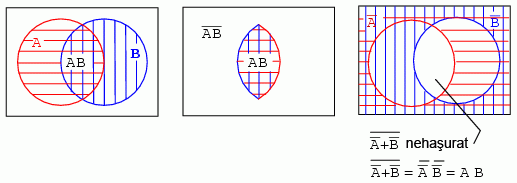
8.3.4 Diagrame Venn cu 3 variabile

Diagrama Venn de mai jos conţine trei regiuni haşurate, A (roşu), B (albastru) si C (verde). Interescţie tuturor regiunilor în centru reprezintă epxresia booleană ABC. Există o altă regiune unde A şi B se intersectează, reprezentând expresia booleană AB. Similar, interescţia ariei A cu C şi B cu C reprezintă expresia booleană AC, reprectiv BC.

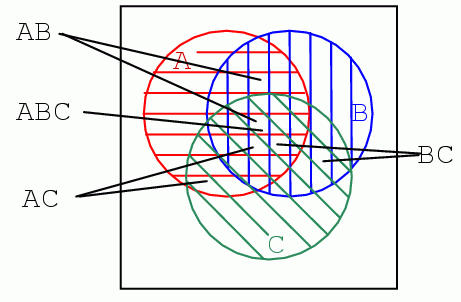
Observând mărimea regiunilor descrise de functia ŞI de mai sus, putem vedea că mărimea regiunii variază cu numărul variabilelor asociate expresiei ŞI.

8.4 Transformarea diagramelor Venn în hărţi Karnaugh

8.4.1 Hărţi Karnaigh cu două variabile

Începem transformarea unei diagrame Venn într-o hartă Karnaugh prin desenarea unei mulţimi A în universul A' (figura de mai jos, a):

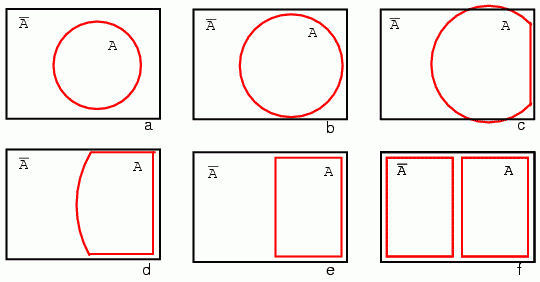
Extindem apoi cercul A (b şi c), modificăm forma lui la punctul (d), şi transformăm A într-un dreptunghi (e). Tot ceea ce nu se află în A este A'. Desenăm un dreptunghi şi pentru A' la punctul (f). De asemenea, nu folosim haşuri pentru hărţile Karnaugh. Ceea ce avem până în acest moment este o hartă Karnaugh cu o singură variabilă. Acest lucru nu ne ajută însă. Avem nevoie de variabile multiple.

Figura (a) de mai jos este identică diagramei Venn precedente, cu diferenţa că notaţiile A şi A' se afla deasupra diagramei şi nu în interior. Urmând un proces similar, putem construi „o diagramă Venn dreptunghiulară” pentru B şi B' (b). Vom trece acum la suprapunerea diagramelor de la (a) şi (b) pentru obţinerea rezultatului (c), la fel cum am facut pentru diagramele Venn. Motivul pentru care realizăm acest lucru este pentru a observa ceea ce este comun celor două regiuni suprapuse - de exemplu, locul în care A se suprapune cu B. Pătratul din dreapta jos (c) corespunde relaţiei AB, unde A se suprapune cu B:

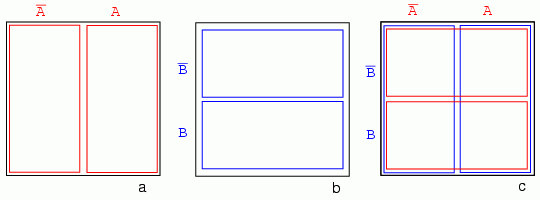
Totuşi, nu vom pierde vremea desenând hărţi Karnaugh precum cea de mai sus (c), ci vom folosi o versiune simplificată:

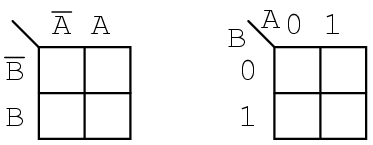
Coloana formată din cele două celule de sub A' este asociată mulţimii A' (stânga); similar pentru celelalte mulţimi. Pentru simplitate, regiunile nu vor fi delimitate atât de clar precum în cazul diagramelor Venn.

Harta Karnaugh din dreapta este o formă alternativă utilizată în majoritatea textelor. Numele variabilelor sunt trecute lângă linia diagonală. A-ul de deasupra diagonalei indică faptul că variabila A (şi A') aparţine coloanelor. 0 este folosit pentru A' iar 1 pentru A. B-ul de sub diagonală este asociat cu liniile: 0 pentru B' şi 1 pentru B.

Exemplu

Marcaţi căsuţele corespunzătoare expresiei booleene AB în diagrama Karnaugh de mai sus cu 1. Soluţie: haşurăm sau încercuim regiunea corespunzătoare lui A; marcăm apoi regiunea corspunzătoare lui B. Intersecţia celor două regiuni reprezintă AB; trecem un 1 în această căsuţă. Nu este însă necesar să încercuim propriu-zis regiunile A şi B:

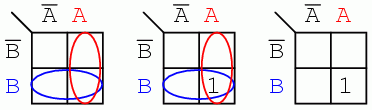
8.4.2 Hărţi Karnaigh cu trei variabile

Trecem acum la dezvoltarea unei hărţi Karnaugh pornind de la diagrame Venn. Universul (interiorul dreptunghiului negru) este împărţit în două regiuni înguste A' şi A. B şi B' împart universul în două regiuni pătrate. C-ul ocupă o regiune pătrată în mijlocul dreptunghiului, iar C' este împărţit în două dreptunghiuri verticale de fiecare parte a pătratului C:

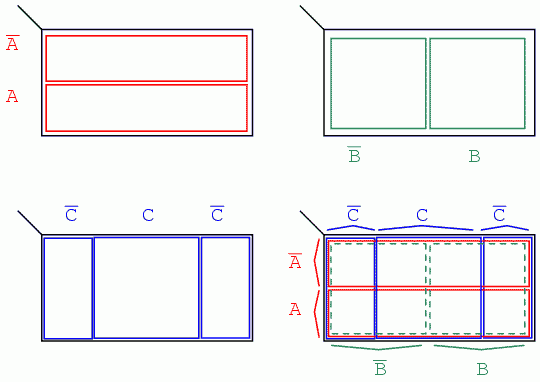
În figura finală suprapunem toate cele trei variabile, încercând să delimităm clar fiecare regiune. Această hartă Karnaugh cu 3 variabile are 2³ = 8 regiuni, căsuţele din interiorul hărţii. Fiecare regiune este unic determinată prin intermediul celor trei variabile booleene (A, B şi C). De exemplu ABC' reprezintă regiunea din dreapta jos (*), iar A'B'C' reprezintă regiunea din stânga sus (x):

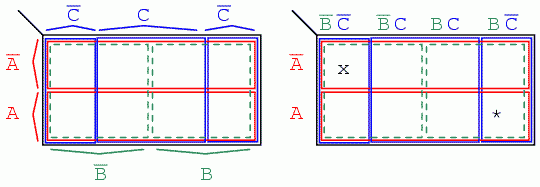
Totuşi, în mod normal nu vom nota o hartă Karnaugh conform figurii de mai sus stânga. Notarea hărţilor Karnaugh se va face conform figurii din dreapta. Fiecare regiune este unic determinată printr-un produs de 3 variabile, o expresie booleană ŞI.

Cele două forme diferite de mai jos sunt echivalente, şi reprezintă forma finală a acestora. Versiunea din dreapta este puţin mai uşor de folosit, din moment ce nu suntem nevoiţi să scriem toate variabilele de fiecare dată, ci doar 1 şi 0. Noaţia B'C', B'C, BC şi BC' din stânga este echivalentă cu 00, 01, 11 respectiv 10 din dreapta. A şi A' sunt echivalente cu 0 respectiv 1.

8.5 Hărţi Karnaugh, tabele de adevăr şi expresii booleene

Hărţile Karnaugh simplifică funcţiile logice mult mai rapid şi mai uşor în comparaţie cu algebra booleană. Dorim simplificarea circuitelor logic spre cel mai mic cost posibil prin eliminarea componentelor. Definim cel mai mic cost ca fiind cel mai mic număr de porţi cu cel mai mic număr de intrări pe poarta.

Mai jos am reprezentat cinci metode diferite de reprezentare a aceluiaşi lucru: o funcţie logică aleatoare cu două intrări. Metodele sunt: logica ladder, porţi logice, tabel de adevăr, hartă Karnaugh şi ecuatie booleană. Ceea ce vrem să sublinem este că toate acestea sunt echivalente. Două intrări A şi B pot lua valori de 0 sau 1, înalt sau jos, deschis sau închis, adevărat sau fals, în funcţie de caz. Există 2² = 4 combinaţii pentru generarea unei ieşiri. Acest lucru se aplică tuturor celor cinci exemple.

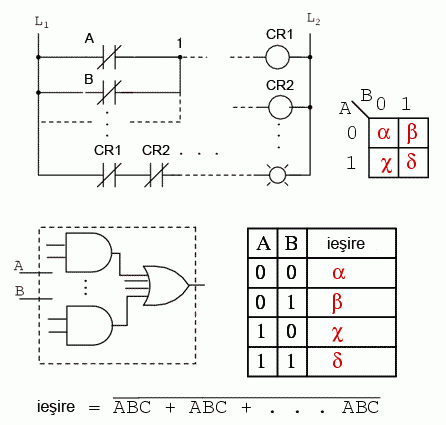
Aceste patru ieşiri pot fi observate prin intermediul unei lampi la ieşirea circuitului ce utilizează logica ladder. Aceste ieşiri pot fi înregistrate într-un tabel de adevăr sau într-o hartă Karnaugh. Priviţi harta Karnaugh ca şi un tabel de adevăr „cosmetizat”. Ieşirea ecuaţiei booleene poate fi obţinută cu ajutorul legilor algebrei booleene şi transferată tabelului de adevăr sau hărţii Karnaugh. Care din cele cinci metode echivalente de reprezentare ar trebui să o folosim? Cea mai folositoare pentru situaţia în cauză.

Ieşirile unui tabel de adevăr corspund unu-la-unu elementelor unei hărţi Karnaugh. Începând cu partea de sus a tabelului de adevăr, intrările A = 0 şi B = 0 produc ieşirea α. Observă că aceeiaşi ieşire, α, se regăseşte pe harta Karnaugh la adresa A = 0, B = 0, în partea de sus stânga, la intersecţia coloanei B = 0 cu rândul A = 0. Celelalte ieşiri ale tabelului de adevăr, β, χ respectiv δ, corespunzătoare intrărilor AB = 01, 10 respectiv 11 au de asemenea corespondent pe harta Karnaugh:

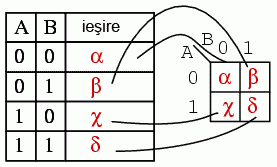
Pentru uşurinţa expunerii, prezentăm mai jos regiunule adiacente ale hărţii Karnaugh cu două variabile folosind metoda dreptunghiulară a diagramei Venn din secţiunea precedentă:

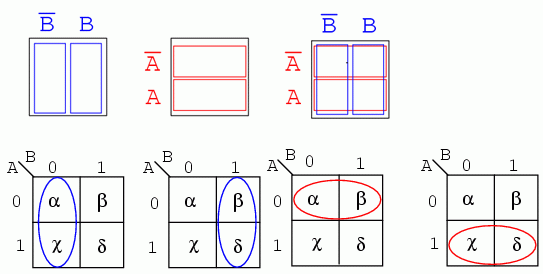
Regiunile α şi χ sunt adiacente pe harta Karnaugh. Nu putem spune acelaşi lucru despre tabelul de adevăr precedent, întrucât există o altă valoare (β) între ele. Acesta este si motivul organizării hărţilor Karnaugh sub formă de matrice pătrată. Regiunile cu variabile booleene comune trebuie să se afla una lângă cealaltă. Această structură este şi trebuie să fie uşor de recunoscut când privim o astfel de hartă, din moment ce α şi χ au variabila B' în comun. Ştim acest lucru deoarece B este 0 (identic cu B') pentru coloana de deasupra celor două regiuni. Comparaţi acest lucru cu diagrama Venn de deasupra hărţii Karnaugh.

În aceiaşi ordine de idei, putem observa că β şi δ au ca şi variabilă comună B (B = 1). Prin urmare, α şi β au în comun variabila booleană A' (A = 0), iar χ şi δ variabila A (A = 1).

Pe scurt, am încercat să grupăm variabilele booleene pe regiuni astfel încât să reiasă elementele lor comune. Hărţile Karnaugh sunt organizate pentru a ne oferi exact această „imagine”.

8.5.1 Exemple de utilizare a hărţilor Karnaugh

Exemplul 1

Tabelul de adevăr de mai jos conţine două valori de 1. Harta Karnaugh trebuie să conţină şi ea tot două valori de 1. Luăm prima valoare de 1 din rândul al doilea al tabelului de adevăr: observaţi adresa AB a tabelului de adevăr; localizaţi regiunea hărţii Karnaugh ce conţine aceiaşi adresă; scrieţi un 1 în acea regiune; repetaţi procesul pentru valoarea 1 din ultima linie a tabelului de adevăr.

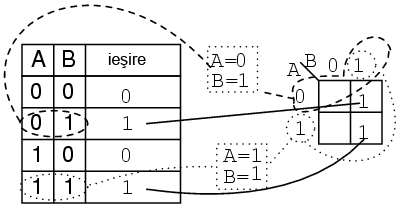
Să încercăm să scriem acum pentru harta Karnaugh de mai sus şi expresia booleană. Soluţia este prezentată mai jos:

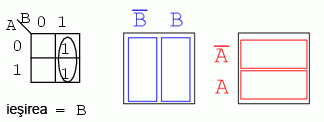
Căutam regiuni adiacente (regiunile diagonale nu sunt adiacente), întrucât acestea vor avea una sau mai multe variabile booleene în comun: grupăm cele două valori de 1 din coloană; căutăm acea sau acele variabile ce sunt comune pentru grup şi scriem acest lucru ca şi rezultat boolean (în cazul nostru acesta este B); ignorăm variabilele ce nu sunt identice pentru un grup de regiuni (în cazul nostru, A variază, este atât 1 cât şi 0, prin urmare, ignorăm A); ignorăm de asemenea orice variabilă ce nu este asociată cu regiunile ce conţin 1 (B' nu conţine niciun 1, prin urmare, ignorăm B'); rezultatul final şi prin urmare expresia booleană asociată hărţii Karnaugh precedente este B. Acest lucru poate fi observa mai uşor comparând diagramele Venn din dreapta, în mod special coloana B.

Exemplul 2

Scrieţi expresia booleană asociată hărţii Karnaugh de mai jos:

Urmând o logică asemănătoare celei de mai sus, grupăm toate valorile de 1 şi găsim variabila comună întregului grup astfel format; rezultatul este A'.

Exemplul 3

Pentru tabelul de adevăr de mai jos, găsiţi harta Karnaugh corespunzătoare şi scrieţi apoi expresia booleană folosind rezultatul obţinut:

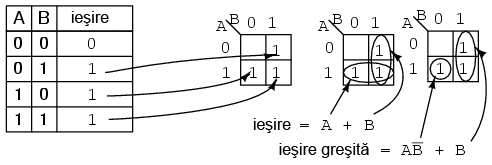
Soluţie: transferăm valorile de 1 din tabelul de adevăr în locaţiile corespunzătoare pe harta Karnaugh; grupăm cele două valori de 1 pe coloana de sub B = 1; grupăm cele două valori de 1 de pe rândul A = 1; scriem rezultatul produsului primului grup (B); scriem rezultatul produsului celui de al doilea grup (A); scriem suma produselor celor doi termeni de mai sus (A + B).

Soluţia din mijloc este cea mai simplă şi prezintă cel mai mic cost. O soluţie mai puţin dorită este cea din dreapta. După gruparea valorilor 1, facem greşeala de a forma un grup cu o singură regiune. Motivul pentru care acest lucru nu este de dorit este următorul: aceast grup ce conţine o singură reziune are termenul produsului egal cu AB'; soluţia întregii hărţii este în aces caz AB' + B, iar aceasta nu reprezintă cea mai simplă soluţie.

Metoda corectă constă în gruparea acestui 1 singur cu regiunea din dreapta lui, regiune ce conţine la rândul ei o valoare de 1, chiar dacă aceasta a fost deja inclusă într-un alt grup. (coloana B). Putem refolosi regiuni pentru a forma grupuri mai mari. De fapt, este chiar indicat să facem acest lucru întrucât conduce la rezultate mai simple.

Trebuie să facem observaţia că oricare dintre soluţiile de mai sus, atât cea corectă cât şi cea „greşită” sunt de fapt corecte din punct de vedere logic. Ambele circuite vor genera aceiaşi ieşire. Pur şi simplu, circuitul corect presupune un cost mai redus de implementare fizică.

Exemplul 4

Completaţi o hartă Karnaugh folosind expresia booleană de mai jos. Scrieţi apoi expresia booleană a rezultatului:

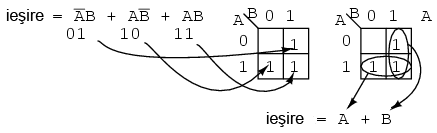
Expresia booleană conţine trei sume de produse. Va exista câte o valoare de 1 pe harta Karnaugh pentru fiecare produs. Deşi, în general, numărul valorilor de 1 pe produs variază cu numărul variabilelor produsului în comparaţie cu mărimea hărţii Karnaugh. Termenul produsului reprezintă adresa regiunii unde vom introduce valoare de 1. Primul termen este A'B şi corespunde adresei 01 a hărţii. Inotroducem un 1 în această regiune. Similar, introducem şi ceilalţi doi termeni de 1.

Trecem apoi la gruparea termenilor şi simplificarea rezultatului conform exemplului precedent.

Exemplul 5

Simplificaţi circuitul logic de mai jos:

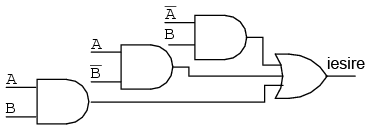
Scriem expresia booleană pentru circuitul logic iniţial; transferăm expresia booleană rezultată într-o hartă Karnaugh; grupăm regiunile precum în exemplele precedente; scriem expresii booleene pentru fiecare grup, conform exemplelor precedente; redesenăm circuitul logic simplificat:

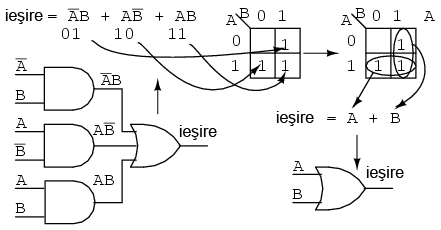
Exemplul 6

Simplificaţi circuitul logic de mai jos:

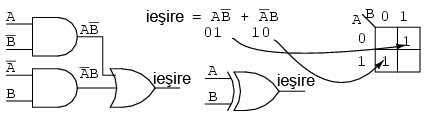
Scriem expresia booleană pentru circuitul logic iniţial; completăm harta Karnaugh; obervăm că nu putem forma niciun grup care să conţină mai mult de două regiuni 1; prin urmare, simplificarea nu este posibilă, iar expresia finală este identică cu cea iniţială (SAU-exclusiv).

8.6 Simplificarea circuitelor logice cu hărţi Karnaugh

Exemplele de simplificare a circuitelor logice de până acum puteau fi realizate la fel de bine şi cu ajutorul algebrei booleene. Problemele de simplificare logică reale implică însă utilizarea unor hărţi Karnaugh mai mari. În această secţiune vom concepe câteva exemple imaginare, lăsând aplicaţiile practice pentru capitolul de logică combinaţională. Aceste exemple sunt concepute doar pentru a ilustra tehnicile de simplificare.

Vom folosi harta Karnaugh dezvoltată anterior, mai exact forma din dreapta:

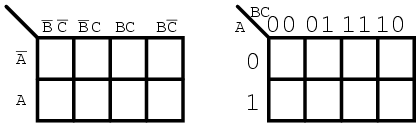
8.6.1 Codul Gray

Observaţi secvenţa numerelor din partea superioară a harţii. Aceasta nu este o secvenţa binară (00, 01, 10, 11), ci este o secvenţă de tipul 00, 01, 11, 10. Această secvenţă este cunoscută sub numele de cod Gray. Secvenţa de tip cod Gray modifică doar un singur bit pe măsură ce trecem de la un număr la următorul număr din secvenţă. Acest lucru nu este valabil într-o secvenţa binară. Regiunile adiacente diferă doar printr-un singur bit, sau variabilă booleană. Acest lucru este necesar dacă dorim organizarea ieşirilor unei funcţii logice pentru observarea elementelor lor comune.

Mai mult, antetul coloanelor şi rândurilor trebuie să fie în ordinea codului Gray, altfel, harta nu se va comporta precum o hartă Karnaugh. Regiunile ce au în comun variabile booleene nu vor mai fi adiacente şi nu vom mai putea identifica carcateristicile specifice funcţiei pe cale vizuală. Regiunile adiacente variază cu un singur bit, deoarece secvenţa de cod Gray variază la rândul ei doar cu un singur bit.

8.6.2 Hărţi Karnaugh cu 3 variabile - exemple de simplificare

Să folosim în continuare hărţile Karnaugh cu 3 variabile pentru simplificarea unor expresii booleene. Vom arăta cum să trecem termenii produs ai ecuaţiei nesimplificate în harta Karnaugh. Vom ilustra şi modul de identificare a grupurilor de regiuni adiacente ce duc la formarea sumei de produse simplificate a circuitului logic (expresiei booleene).

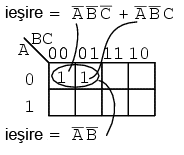
Dându-se expresia (A'B'C' + A'B'C), primul pas este introducerea valorilor de 1 pe harta Karnaugh corespunzător poziţiei fiecărui produs al sumei (A'B'C' este echivalent cu 000, iar A'B'C este echivalent cu 001). Identificăm apoi un grup de regiuni alăturate ce conţin valori de 1 (în cazul de faţă, avem doar două astfel de regiuni). Scriem apoi produsul de termeni pentru acest grup, ceea ce reprezintă rezultatul simplificat.

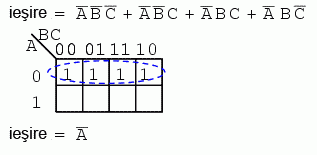
Grupând cei patru termeni de 1 pe harta Karnaugh, rezultatul este asigurat de expresia A'.

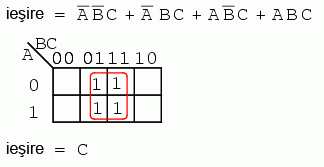
Identic, grupând ce patru termeni de 1, putem foarte uşor observa că singura variabilă ce acoperă toate cele patru regiuni este C.

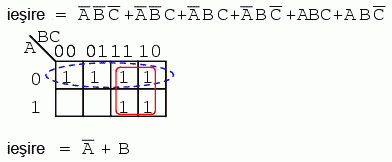
Din moment ce avem două grupuri pe harta Karnaugh de mai sus, rezultatul va fi o sumă de produse, şi anume, A' + B.

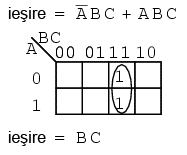
Cele două produse de mai sus formează un grup de doi termeni ce se simplifică la BC.

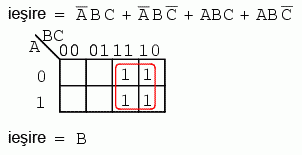
Variabila comună celor patru termeni grupaţi mai sus este B

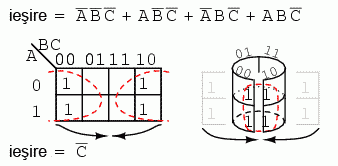
Cei patru termeni de mai sus formează un singur grup. Putem vizualiza acest grup dacă îndoim extremităţile hărţii pentru a forma un cilindru. În acest caz, regiunile sunt adiacente. În mod normal, un astfel de grup se notează conform figurii din stânga. Din întregul set de variabile (A, B, C), singura variabilă comună este C'. C' este zero în toate cele patru regiuni. Acesta este atunci rezultatul final al simplificării.

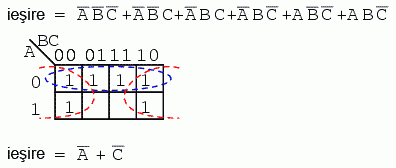
Cele şase regiuni rezultate din ecuaţia nesimplificată pot fi organizate în două grupuri de câte patru. Aceste grupuri trebuie să rezulte într-o sumă de două produse, şi anume A' + C'.

8.6.3 Incinerator deşeuri toxice - reconsiderare

Să reluăm mai jos exemplul incineratorului de deşeuri toxice studiat într-un capitol precedent. Vom încerca simplificarea circuitului logic folosind o hartă Karnaugh:

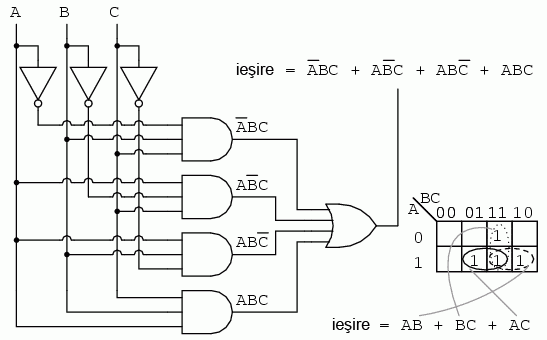
Ecuaţia booleană de iesire este o sumă de patru produse. Prin urmare, vom avea patru regiuni de 1 pe harta Karnaugh. Grupând regiunile adiacente, avem trei grupuri de câte doi termeni. Vom avea prin urmare o sumă de trei produse, fiecare produs conţinând doi termeni. Circuitul logic simplificat, identic cu cel obţinut cu ajutorul regulilor de simlificare booleană, este redat mai jos:

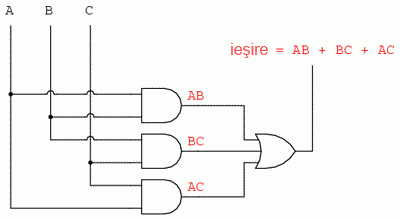
Făcând o comparaţie între regulile boolene folosite pentru simplificarea circuitului logic al incineratorului…

…şi harta Karnaugh, care duce la exact acelaşi rezultat…

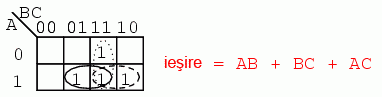
Putem lesne vedea motivul pentru care hărţile Karnaugh sunt preferate pentru simplificarea circuitelor logice în detrimentul simplificării booleene.

8.7 Hărţi Karnaugh de patru variabile

Folosindu-ne de codul Gray, putem construi hărţi Karnaugh mai mari. O hartă Karnaugh cu patru variabile arată precum cea de mai jos:

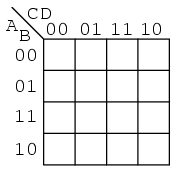
Exemplele de mai jos ilustrează simplificarea expresiilor booleene ce sunt prea greu de realizat prin intermediul regulilor de simplificare booleană. Aceste expresii pot fi simplificate cu algebra booleană. Totuşi, utilizarea hărţilor Karnaugh este un procedeu mult mai rapid si mai uşor, mai ales dacă există multe simplificări logice de realizat.

8.7.1 Exemple de simplificare logică cu hărţi Karnaugh de patru variabile

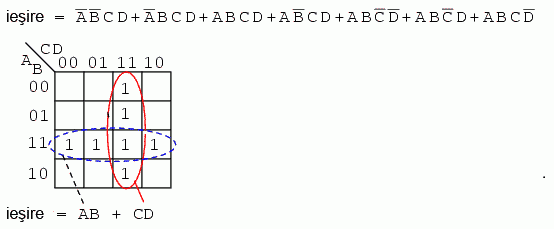
Expresia booleană de mai sus conţine 7 produse. Aceşti termeni sunt grupaţi de sus în jos şi de la stânga la dreapta pe harta Karnaugh de mai sus. De exemplu, primul termen, A'B'CD, se regăseşte pe rândul 1, căsuţa a 3-a, şi corespunde locaţiei A = 0, B = 0, C = 1, D = 1. Ceilalţi termeni sunt poziţionaţi într-o manieră similară. Grupul orizontal (albastru) corespunde termenului AB, iar grupul vertical (roşu) corespunde expresiei booleene CD. Din moment ce avem două grupuri, rezultatul trebuie să fie o sumă de două produse, prin urmare, AB + CD.

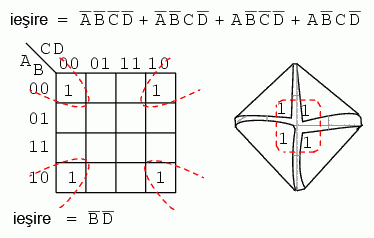
În cazul de mai sus, „împăturim” cele patru colţuri ale hărţii Karnaugh, precum un şerveţel, pentru a observa mai bine adiacenţa celor patru regiuni. B = 0 şi D = 0 pentru toate regiunile. Celelalte variabile, A şi B, sunt 0 în unele cazuri şi 1 în altele. Prin urmare, aceste variabile nu se vor regăsi în rezultatul final al expresiei simplificate.

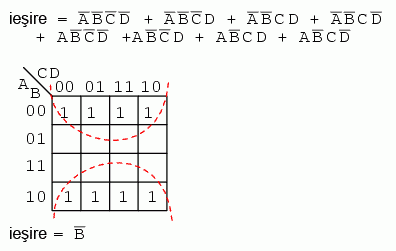
Pentru o vizualizare mai bună, ne putem imagina că îndoim marginile de jos şi de sus a hărţii sub forma unui cilindru. În acest caz, ambele grupuri sunt adiacente şi formează practic un singur grup. Acest lucru ne spune că rezultatul este un singur termen. Singura variabilă comună a acestui grup de 8 variabile este B = 0. Rezultatul simplificării este prin urmare B'.

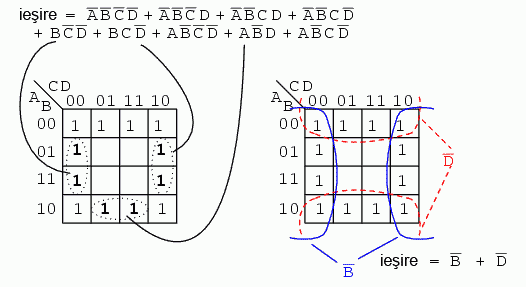
Expresia booleană de mai sus conţine 9 termeni de produse, dintre care trei au doar trei variabile booleene în loc de patru. Diferenţa constă în faptul că, deşi termenii ce conţin patru variabile booleene acoperă o singură regiune, termenii cu trei variabile booleene acoperă o pereche de regiuni fiecare.

Trecând la simplificare, formăm două grupuri de câte opt termeni. Regiunle ce se regăsesc în colţ sunt comune ambelor grupuri. Acest lucru este corect. De fapt, această strategie conduce la o soluţie mai bună decât dacă am fi format un grup de opt şi un grup de patru regiuni, fără nicio regiune comună celor două. Soluţia finală este B' + D'.

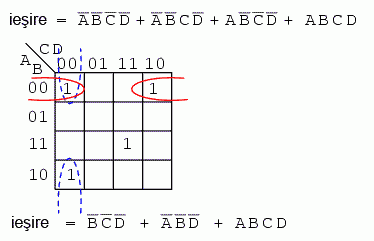
În exemplul de mai sus, trei regiuni formează două grupuri de câte două. O a patra regiune nu poate fi combinată cu nicio altă regiune, ceea ce se întâmplă frecvenţe în situaţiile reale. În acest caz, termenul ABCD rămâne neschimbat în cadrul procesului de simplificare a expresiei booleene iniţiale. Rezultatul este B'C'D' + A'B'D' + ABCD.

Adeseori, există mai mult de o singură soluţie cu cost minim pentru expresia nesimplificată. Un astfel de caz este cel de mai jos:

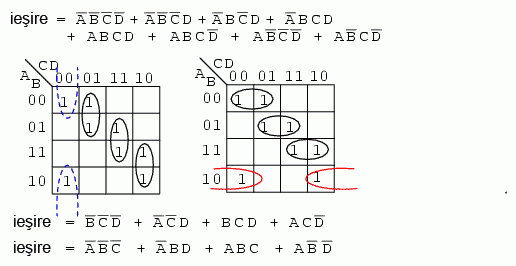
Ambele rezultate de mai sus conţin patru termeni, cu trei variabile booleene fiecare. Ambele soluţii sunt valide din punct de vedere al minimizării costurilor. Diferenţa dintre cele două soluţii finale constă în modul de grupare al regiunilor. Reamintim faptul că o soluţie cu cost minim este acea soluţie ce permite o implementare fizică a circuitului logic cu un număr cât mai mic de porţi logice şi număr de intrări.

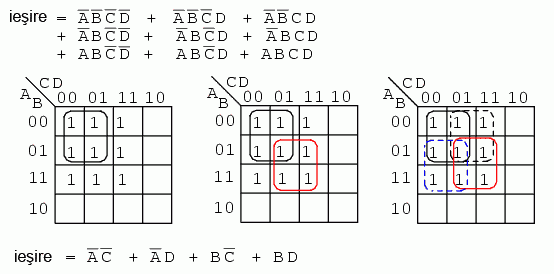
În următorul exemplu, cel de mai sus, după ce trecem toate valorile de 1 pe hartă Karnaugh, realizăm primul pas al simplificării, şi anume, gruparea primelor patru regiuni (stânga). În acest punct, s-ar putea să nu fie foarte evident cum am putea grupa regiunile rămase.

La pasul al doilea (centru), grupăm încă patru regiuni. Mai rămân în acest moment încă două regiuni negrupate. Soluţia cu cost minim este să grupă aceste două regiuni, ca şi grupuri de patru, conform figurii din dreapta.

Atenţie, nu încercaţi să realizaţi grupuri de câte trei. Grupările trebuie să fie sub forma puterilor lui 2, şi anume, 1, 2, 4, 8, etc.

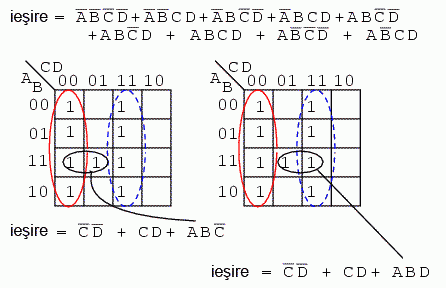
Avem din nou mai sus un exemplu ce suportă două soluţi cu cost minim. Formăm iniţial cele două grupuri de câte patru regiuni (roşu şi albastru). Soluţia finală depinde de modul în care grupăm regiunea rămasă liberă. Dacă o introducem în grupul din stânga (roşu), soluţia este ABC'. Dacă o întroducem în grupul din dreapta (albastru), soluţia este ABD. Indiferent de alegerea făcută, ambele soluţii sunt corecte din punct de vedere al minimizării costurilor de implementare.

Mai sus este un exemplu de simplificare cu hărţi Karnaugh (stânga) precum şi cu regulile algebrei booleene (dreapta). C' (C = 0) reprezintă aria formată de cele opt regiuni din stânga. Regiunea rămasă negrupată este echivalentă cu expresia ABCD. Grupând această regiune cu cea din stânga ei, simplifă termenul ABCD la ABD. Rezultatul final este prin urmare C' + ABD.

Cazul de mai sus este un exemplu rar a unei probleme cu patru variabile ce poate fi redusă destul de uşor şi cu algebra booleană. Asta în cazul în care vă amintiţi teoremele de simplificare booleană.

8.8 Mintermeni şi maxtermeni

Până în acest moment am căutat soluţii sub forma unei sume de produse la problemele de simplificare booleană. Pentru fiecare dintre aceste soluţii există o altă soluţie sub forma unui produs de sume. Acest tip de soluţie se poate dovedi a fi mai practică, în funcţie de aplicaţie. Dar, înainte de a scrie soluţiile sub forma unui produs de sume, trebuie să introducem câteva concepte noi. Procedura de mai jos pentru extragerea termenilor sub formă de produs nu este nouă. Vrem doar să stabilim o procedură formală pentru mintermeni, ca mai apoi, să putem face o comparaţie cu noua procedură pentru maxtermeni.

8.8.1 Analiza regiunilor ce conţin valori de 1 - mintermeni

Un mintermen este o expresie booleană rezultând într-o valoare de 1 pentru ieşirea unei singure regiuni dintr-o hartă Karnaugh. Toate celelalte regiuni ale hărţii Karnaugh sau ale tabelului de adevăr fiind 0 în acest caz. Dacă un mintermen conţine un singur 1, iar regiunile rămase sunt toate 0, aria minimă pe care acest minterm o acoperă este 1.

Figura de mai jos (stânga) prezintă mintermenul ABC, un singur termen sub formă de produs, ca şi o singură valoare de 1 pe o hartă Karnaugh unde toate celelalte regiuni sunt 0. Până în acest moment, nu am prezentat valorile de 0 pe hărţile Karnaugh considerate. Acestea se omit de obicei, excepţie făcând cazurile speciale. Un alt mintermen, A'BC' este cel din dreapta. Ceea ce vrem să subliniem este faptul că adresa regiunii corespunde direct cu mintermenul extras de pe hartă. Regiunea 111 corespunde mintermenului ABC din stânga. Regiunea 010 corespunde la rândul ei mintermenului A'BC'. O expresie booleană sau o hartă poate avea mai mulţi mintermeni.

Referindu-ne la figura de mai sus, putem scrie procedura introducerii unui mintermen pe harta Karnaugh:

Identificăm mintermenul (produsul) ce vrem să-l introducem pe hartă
Scriem valoarea numerică corespunzătoare
Ne folosim de valoarea binară ca şi adresă pe hartă
Introducem un 1 la adresa respectivă
Repetăm paşii de mai sus pentru un nou mintermen (termenii produs dintr-o sumă de produse)

O expresie booleană este formată de cele mai multe ori din mai mulţi mintermeni, corespunzând mai multor regiuni pe o hartă Karnaugh, precum în exemplul de mai jos:

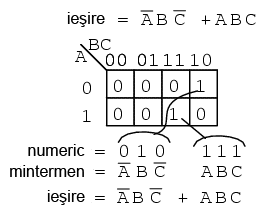
Mintermenii multiplii de pe această hartă sunt mintermenii individuali ce i-am analizat mai sus. Ceea ce vrem să reamintim este faptul că valorile de 1 sunt „traduse” de pe harta Karnaugh ca şi o adresă binară transformată direct într-unul sau mai mulţi termeni sub formă de produs. Prin direct, ne referim la faptul că 0 corespunde unei variabile negate, iar 1 corespunde unei variabile „pure”. De exemplu, 010 se transformă direct în A'BC'. În acest exemplu nu a existat nicio simplificare. Totuşi, avem ca şi rezultat o sumă de produse prin intermediul mintermenilor.

Referindu-ne la figura de mai sus, putem rezuma pe scurt procedura de urmat în cazul simplificării expresiei booleene sub forma unei sume de produse dintr-o hartă Karnaugh:

Formăm grupuri de 1 cât mai mari posibile, acoperind toţi mintermenii de pe hartă. Grupurile trebuie să conţină un număr de regiuni sub forma puterii lui 2 (1, 2, 4, 8, etc.)
Scriem valori numerice binare pentru fiecare grup
Transformăm valoarea binară sub forma unui produs
Repetăm paşii de mai sus pentru toate grupurile formate. Din fiecare grup va rezulta un termen sub formă de produs
Expresia simplificată reprezintă suma acestor termeni sub formă de produs

Nimic nou până în acest moment. Am scris doar paşii de urmat în cazul mintermenilor. Acelaşi lucru îl vom face şi în cazul maxtermenilor.

8.8.2 Analiza regiunilor ce conţin valori de 0 - maxtermeni

Să considerăm acum o funcţie booleană ce este 0 pentru o singură regiune şi 1 în rest:

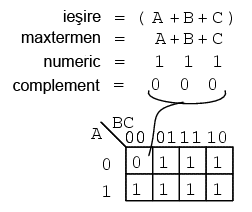
Un maxtermen este o expresie booleană a cărei valori este 0 pentru o singură regiune, toate celelalte regiunii ale hărţii Karnaugh sau ale tabelului de adevăr fiind 0. Vedeţi şi explicaţia de la mintermen. Figura de sus stânga prezintă un maxtermen (A + B + C), o sumă de trei termeni simplii. Pe hartă, această sumă este reprezentată printr-un singur 0, toate celelalte regiunii ale hărţii fiind 1. Dacă un maxtermen are un singur 0, iar celelalte regiuni sunt 1, aria maximă pe care o acoperă este 1.

Există câteva diferenţe acum că am introdus şi maxtermenii. Maxtermenul este un 0, nu un 1 pe harta Karnaugh. Un maxterm este un termen sub formă de sumă, A + B + C în cazul nostru, şi nu termen sub formă de produs (ABC, de exemplu).

Pare ciudat că locaţia expresiei (termenului) (A + B + C) pe hartă este

Pentru ecuaţia „ieşire = (A + B + C) = 0, toate cele trei variabile

(A, B, C) trebuie să fie egale cu 0. Doar expresia (0 + 0 + 0) = 0 va fi egală cu 0. Prin urmare, trecem singurul nostru maxtermen (A + B + C) în regiunea ce se află la adresa A,B,C = 000 pe harta Karnaugh, unde toate intrările sunt egale cu 0. Aceasta este singura posibilitate pentru a obţine valoarea de 0 pentru maxtermen. Toate celelalte regiuni conţin valori de 1 pentru că orice alte valori de intrare diferite de (0, 0, 0) pentru expresia (A + B + C) au ca şi rezultat 1.

Luând în considerare figura de mai sus, paşii care trebuiesc urmaţii pentru introducerea unui maxtermen pe harta Karnaugh, sunt următorii:

Identificăm termenul sub formă de sumă (maxtermenul) ce-l vom introduce pe hartă
Scriem valoarea numerică binară corespunzătoare
Formăm complementul
Utilizăm complementul ca şi adresă pentru introducerea valorii de 0 pe harta Karnaugh
Repetăm paşii de mai sus pentru toţi ceilalţi maxtermeni (termeni-sumă dintr-o expresie sub forma de produs de sume)

Un alt maxtermen este prezentat în figura de mai jos. Valoarea numerică 000 corespunde termenului A' + B' + C'. Complementul este 111. Introducem o valoare de 0 pentru maxtermenul (A' + B' + C') la această adresă (1, 1, 1) a hărţii Karnaugh de mai jos:

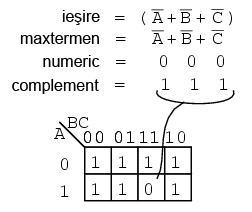
8.8.3 Scrierea expresiei booleene simplificate ca şi produs de sume

O expresie booleană sub formă produsului de sume poate avea mai mulţi maxtermeni, conform figurii de mai jos:

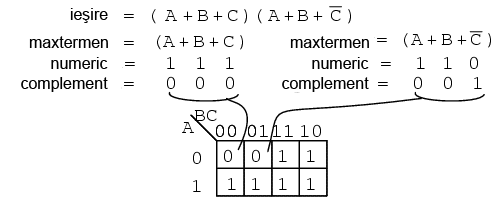
Maxtermenul (A + B + C) sub formă numerică este 111, iar complementat este 000. Plasăm prin urmare un 0 la adresa (0, 0, 0). Maxtermenul (A + B + C') sub formă numerică este 110, iar complementat este 001. Plasăm prin urmare un zero la adresa (0, 0, 1).

Acum că am construit harta Karnaugh, suntem interesaţi de modul în care putem scrie o formă simplificată a expresiei booleene iniţiale sub formă de produs de sume. Primul pas este gruparea termenilor de 0, precum grupul de mai jos:

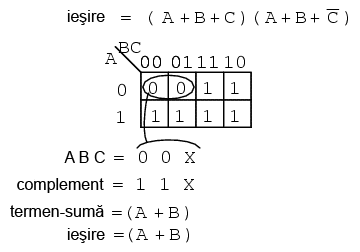
Scriem apoi valoarea binară corespunzătoare termenului-sumă, ce arată astfel: (0, 0, X). Pentru grupul format, atât A cât şi B sunt 0. Dar C este atât 0 cât şi 1. Prin urmare, scriem un X în locul valorii lui C. Formăm complementul: (1, 1, X). Scriem termenul sumă (A + B) ignorând C-ul si X-ul ce l-a înlocuit.

Să reluăm paşii necesari pentru reducerea unei expresii booleene la un produs de sume:

Formăm grupuri de 0 cât mai mari posibile, incluzând toţi maxtermenii. Numărul termenilor trebuie să fie puteri ale lui 2
Screim valoarea numerică a grupului
Complementăm această valoare numerică a grupului
Transformăm valoarea complementată într-un termen sub formă de sumă
Repetăm paşii de mai sus pentru toate grupurile rămase pe hartă. Rezultatul fiecărui grup este un termen sub formă de sumă, iar rezultatul final este produsul acestor termeni-sumă

Exemplul 1

Simplificaţi expresia booleană sub forma produsului de sume de mai jos. Scrieţi rezultatul final sub forma unui produs de sume:

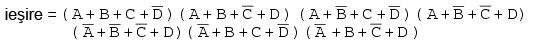
Soluţie: completăm o hartă Karnaugh cu cei şapte maxtermeni de mai sus (introducem valori de 0). Reţineţi să complementaţi variabile de intrare pentru găsirea adresei corespunzătoare:

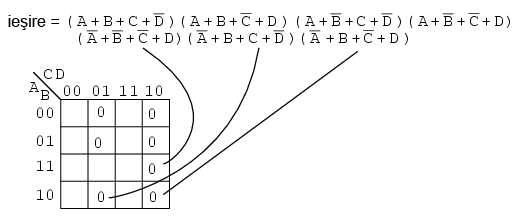
După ce am introdus toţi maxtermenii în tabel, trecem la gruparea regiunilor, precum în figura de mai jos. Grupurile mai mari se traduc printr-un termen-sumă cu mai puţine intrări. Cu cât avem mai puţine grupuri, cu atât vom avea mai puţin termeni-sumă în expresia finală:

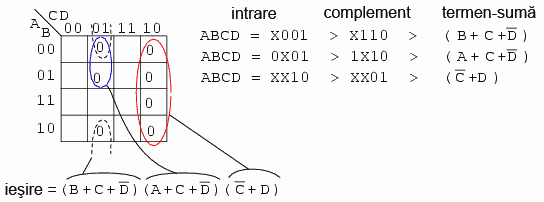
Avem trei grupuri, prin urmare, trebuie să avem trei termeni-sumă în rezultatul final. Detaliile simplificării sunt prezentate în figura de mai sus. Pentru oricare grup, scriem mai întâi adresa de intrare, o comlementăm şi o transformăm într-un termen boolean sub formă de sumă. Rezultatul final este produsul acestor trei termeni-sumă.

Exemplul 2

Simplificaţi expresia booleană sub formă de produs de sume de mai jos, exprimând rezultatul sub forma unei sume de produse:

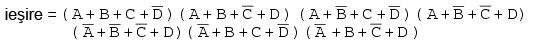
Această problemă este identică cu cea anterioară, cu diferenţa că expresia simplificată se cere sub formă de sumă de produse şi nu sub formă de produs de sume.

Trecem maxtermenii (0) din expresia iniţială pe harta Karnaugh de mai jos (stânga), exact ca în exemplul precedent:

Completăm apoi toate celelalte regiuni rămase libere cu valori de 1 (dreapta sus).

Formăm grupuri de 1 pentru toate regiunile ce conţin valori de 1. Scriem apoi rezultatul simplificat sub forma sumei de produse, conform secţiunii precedente a acestui capitol. Acest lucru este identic problemei precedente:

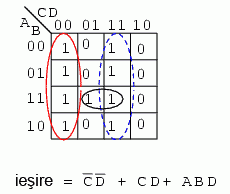
8.8.4 Comparaţie între soluţiile cu mintermeni şi maxtermeni

În figura de mai jos sunt ambele soluţii ale exemplelor de mai sus, pentru comparaţie:

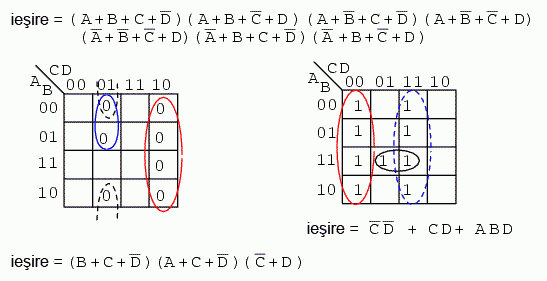
Care soluţie este mai simplă? Dacă ar fi să implementăm fizic rezultatul sub formă de produs de sume, am avea nevoie de trei porţi logice SAU şi o poartă logică ŞI. Invers, darcă ar fi să implementăm rezultatul sub formă de sumă de produse, am avea nevoie de trei porţi ŞI şi o poartă SAU. În ambele situaţii am avea nevoie de patru porţi. Să numărăm atunci şi numărul de intrări ale porţilor. Prima variantă utilizează 8 intrări, iar a doua 7 intrări. Din definiţia costului minim, soluţia sub forma sumei de produse este mai simplă. Acesta este un exemplu tehnic corect, dar care nu ne este de prea mare folos în realitate.

Soluţia „corectă” depinde însă de complexitate şi de familia de porţi logice folosite. Soluţia sumei de produse este mai bună facă folosim circuite TTL, a căror porţi principale sunt porţile ŞI-negat. Acestea sunt foarte bune pentru implementări sub forma de sumă de produse. Pe de altă parte, soluţia produsului de sume este acceptabilă dacă folosim circuite CMOS, deoarece avem astfel la dispoziţie porţi SAU-negat de toate mărimile.

8.8.5 Echivalenţa circuitelor ŞI-SAU cu circuitele ŞI-negat-ŞI-negat

Circuitele cu porţi logice pentru ambele cazuri sunt prezentate mai jos, produsul de sume în stânga şi suma de produse în dreapta:

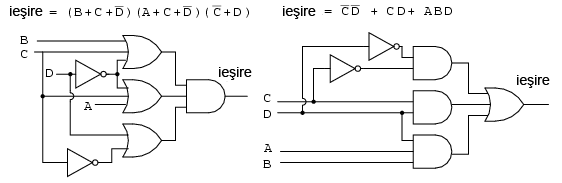
Reluăm mai jos (stânga) circuitul sub forma sumei de produse:

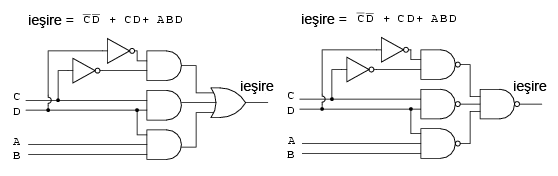
Dacă înlocuim toate porţile logice ŞI din stânga cu porţi logice ŞI-negat, obţinem rezultatu din dreapta sus. Poarta SAU de la intrare este înlocuită de asemenea cu o poartă ŞI-negat. Pentru a demonstra că logica ŞI-SAU este echivalentă cu logică ŞI-negat-ŞI-negat, este suficient să mutăm „cerculeţele” inversoare de la ieşirea celor trei porţi ŞI-negat la intrarea porţii finale ŞI-negat, conform figurii de mai jos:

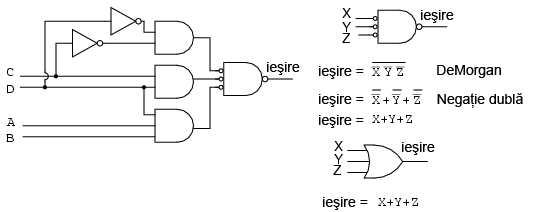
În figura de mai sus (dreapta), putem observa că ieşirea unei porţi SI-negat cu intrări inversate este echivalentă din punct de vedere logic cu o poartă SAU, conform teoremei lui DeMorgan şi a negaţiei duble. Această informaţie ne este de ajutor în implementarea fizică a circuitelor digitale atunci când dispunem de circuite logice TTL cu porţi ŞI-negat.

Paşii necesari construirii logicii ŞI-negat-ŞI-negat în locul logicii ŞI-SAU, sunt următorii:

Realizăm un circuit logic (teoretic) sub formă de sumă de produse
Când desenăm diagrama logică, înlocuim toate porţile logice (ŞI si SAU) cu porţi logice ŞI-negat
Intrările nefolosite trebuie legate la valoarea logică „înalt”
În caz de defect, nodurile interne de la primul nivel de ieşire al porţilor ŞI-negat nu sunt identice cu valorile diagramei ŞI-SAU, ci sunt inversate. Folosim diagrama logică ŞI-negat-ŞI-negat. Intrările şi ieşirile finale sunt identice, totuşi
Notăm fiecare capsulă (circuit integrat) cu U₁, U₂, etc.
Folosim catalogul producătorului pentru conectarea pinilor circuitului integrat la intrările si ieşirile porţilor din circuit

Exemplul 1

Să reluăm o problemă precedentă ce implică o simplificare sub formă sumei de produse. Vom realiza o simplificare sub forma unui produs de sume de această dată. Putem compara cele două soluţii la final.

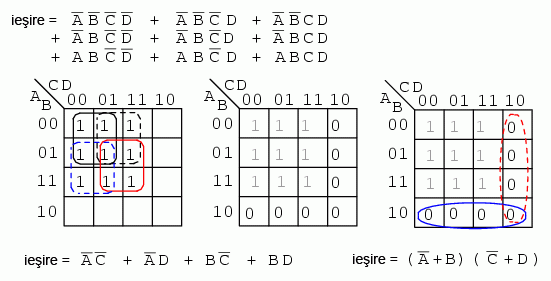
Soluţie: în figura de sus stânga avem problema iniţială, o expresie booleană cu 9 mintermeni nesimplificată. Recapitulând, am format patru grupuri de câte patru regiuni fiecare. Rezultatul a fost o sumă de patru produse (partea din stânga, jos).

În figura din mijloc, completăm regiunile rămase libere cu valori de 0. Formăm două grupuri de câte patru regiuni. Grupul de jos (albastru) este A' + B, iar grupul din dreapta (roşu) este C' + D. Rezultatul este prin urmare un produs de două sume, (A' + B)(C' + D).

Comparând cele două soluţii de mai sus, putem observa că soluţia produsului de sume reprezintă soluţia cu cel mai mic cost. Pentru implementarea primei soluţii am avea nevoie de 5 porţii, iar pentru soluţia produsului de sume am avea nevoie doar de 3. Folosind circuite logice TTL, aceasta din urmă este şi atractivă datorită simplităţii rezultatului. Putem găsim porţi logice ŞI şi SAU cu 2 intrări. Mai jos sunt prezentate circuitele logice pentru ambele soluţii

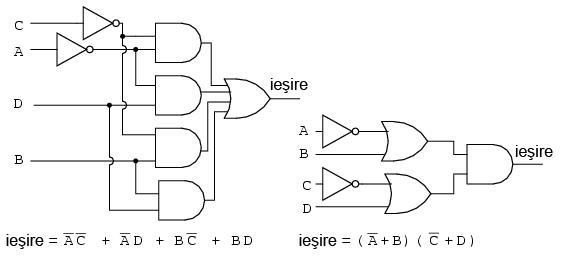
Să presupunem că avem la dispoziţie circuitele logice TTL de mai jos. În acest caz, cunoaştem şi poziţionarea porţilor logice în interiorul acestora, precum în figura de mai jos:

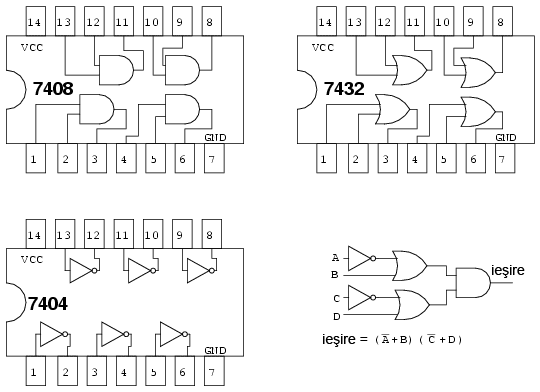
Circuitele integrate folosite (trei la număr) vor fi identificate prin notaţia U1, U2 respectiv U3. Pentru a face distincţie între porţile individuale din fiecare capsulă, acestea vor fi identificate prin a, b, c, d, etc. Circuitul inversor 7404 va fi U₁. Porţile inversoare individuale sunt U1-a, U1-b, U1-c, etc. Circuitul SAU 7432 va fi notat cu U2, iar U3 este notaţie folosită pentru circuitul ŞI 7408.

Luând în considerare piningul circuitelor logice folosite mai sus, vom desemna toate intrările şi ieşirile circuitului logic ce vrem să-l construim, conform figurii de mai jos (intrările porţilor nefolosite se vor lega la masă):

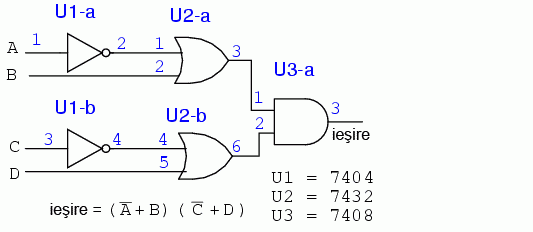
Putem găsi cu uşurinţă porţi logice ŞI cu două intrări (7408, stânga). Totuşi, este mai greu să găsim o poartă logică SAU cu patru intrări. Singurul tip de poartă cu patru intrări este un circuit TTL 7420 cu porţi ŞI-negat (dreapta):

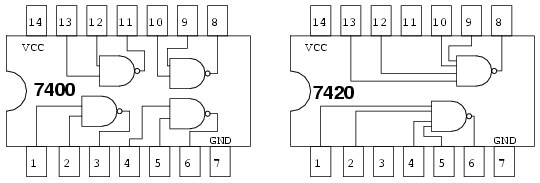
Putem transforma poarta logică ŞI-negat cu patru intrări într-o poartă logică SAU cu patru intrări prin inversarea intrărilor acesteia:

Putem prin urmare folosi circuitul 7420 cu porţi logice ŞI-negat cu patru intrări ca şi poartă SAU prin negarea (inversarea) intrărilor.

Nu vom folosi porţi logice inversoare discrete pentru inversarea intrărilor circuitului 7420. Vom folosi în schimb porţi logice ŞI-negat cu două intrări în locul porţilor ŞI din soluţia booleană cu mintermeni (sumă de produse). Inversarea ieşirii porţilor ŞI-negat cu două intrări este suficientă pentru inversarea necesară realizării porţii logice SAU cu patru intrări:

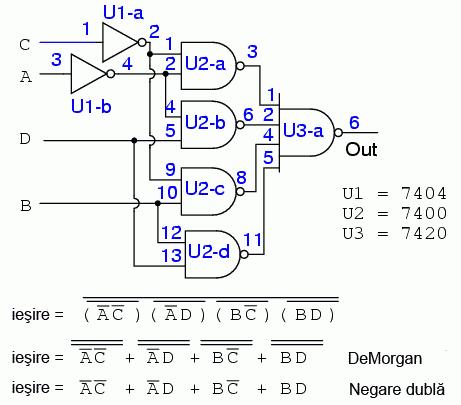
Rezultatul de mai sus este singura modalitate practică de realizarea a circuitului folosind TTL cu porţi logice ŞI-negat-ŞI-negat în locul porţilor ŞI-SAU.

8.9 Notaţia Σ (sumă) şi notaţia Π (produs)

Ca şi referinţa, această secţiune introduce terminologia folosită în unele texte pentru descrierea mintermenilor şi maxtermenilor aparţinând hărţilor Karnaugh. Mai departe de atât, această secţiune nu conţine nimic nou.

8.9.1 Notaţia Σ (sumă) pentru mintermeni

Simbolul Σ (sigma) indică o sumă iar litera „m” indică mintermenii. Prin urmare, Σm reprezintă o sumă de mintermeni. Următorul exemplu ilustrează afirmaţia de mai sus. În loc de ecuaţie booleană, am ales să enumerăm mintermenii:

f(A,B,C,D) = Σ m(1, 2, 3, 4, 5, 7, 8, 9, 11, 12, 13, 15), sau
f(A,B,C,D) = Σ(m1, m2, m3, m4, m5, m7, m8, m9, m11, m12, m13, m15)

Indicii termenilor indică locaţia regiunii, sau adresa, dintr-o hartă Karnaugh. Acesta este cu siguranţa un mod mult mai compact pentru descrierea mintermenilor sau regiunilor unei hărţi Karnaugh.

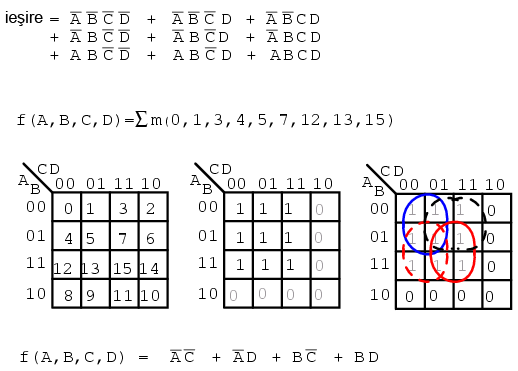
Soluţia exprimată sub formă sumei de produse nu este afectată prin utilizarea acestei terminologii. Mintermenii de pe harta (valorile de 1) sunt grupaţi ca de obicei, iar mai apoi putem scrie o soluţie sub forma sumei de produse.

8.9.2 Notaţia Π (produs) pentru maxtemeni

Mai jos luăm în considerare şi terminologia folosită pentru descrierea unei liste de maxtermeni. Produsul este indicat prin litera Π (pi), iar „M” indică maxtermenii. Prin urmare, ΠP indică un produs de maxtermeni. Putem folosi acelaşi exemplu pentru ilustrarea celor spuse mai sus. Ecuaţia logică booleană nesimplificată este înlocuita cu o listă de maxtermeni:

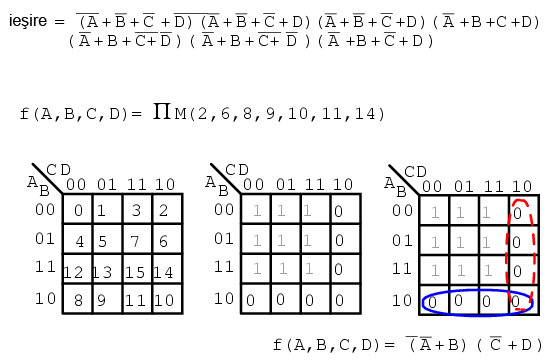
f(A,B,C,D) = Π M(2, 6, 8, 9, 10, 11, 14), sau
f(A,B,C,D) = Π(M2, M6, M8, M9, M10, M11, M14)

Din nou, numerele indică adresa sau locaţia pe harta Karnaugh. Pentru maxtermeni, acestea reprezintă locaţiile valorilor de 0. Soluţia sub forma produsului de sume se scrie ca de obicei.

8.10 Hărţi Karnaugh de 5 şi 6 variabile

Pentru reducerea circuitelor logice mai mari se folosesc, evident, hărţi Karnaugh mai mare. Dar care este mărimea maximă (practică) a unei hărţi Karnaugh? Acest lucru depinde de numărul de intrări a circuitului logic considerat. Practic, se poate constata că această limită este de 6 intrări. Prezentăm mai jos aşadar hărţile Karnaugh de 5 şi 6 variabile.

8.10.1 Harta Karnaugh de 5 variabile

Prima variantă a hărţii Karnaugh de 5 variabile este modelul în oglindă. Desigur, numerotarea se realizează în cod Gray (partea de sus). Acesta se reflectă aproximativ la mijlocul hărţii. Acest stil este folosit de textele mai vechi:

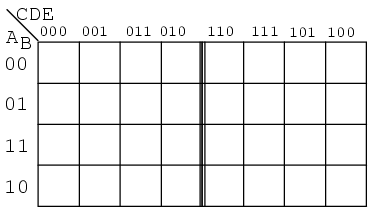
Varianta preferată, cea cu suprapunere, este prezentată mai jos:

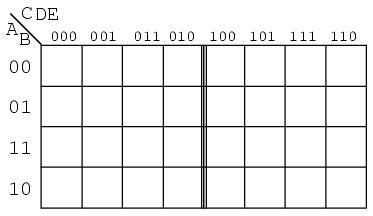
Această variantă constă pur şi simplu din două (patru pentru o hartă Karnaugh de 6 variabile) hărţi identice, cu excepţia bitului cel mai semnificativ din adresa de 3 biţi din partea superioară. Dacă ne uităm în partea de sus a hărţii, observăm că numerotaţia este diferită faţa de harta precedentă (în cod Gray). Dacă ignorăm bitul cel mai semnificativ, precum am spus mai sus, secvenţa 00, 01, 11, 10 se regăseşte în partea superioară a ambelor sub-hărţi. Secvenţa formată din cele opt numere de 3 biţi nu este cod Gray.

Harta Karnaugh cu 5 variabile - exemplu

Să proiectăm un circuit cu 5 intrări binare (A, B, C, D, E), A fiind bit-ul cel mai semnificativ. Circuitul va trebui să producă o ieşire „înaltă” pentru orice număr prim detectat la intrare:

Prezentăm mai jos o soluţie sub forma hărţii Karnaugh de 5 variabile în oglindă, folosind cod Gray:

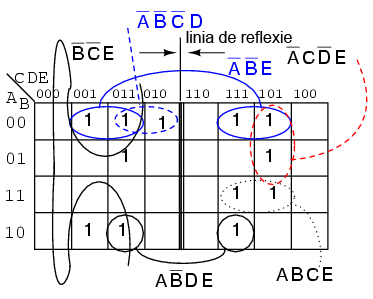
Numerele prime sunt (1,2,3,5,7,11,13,17,19,23,29,31). Introducem o valoare de 1 în fiecare regiune corespunzătoare. Trecem apoi la gruparea regiunilor şi scrierea rezultatului simplificat. Observaţi că grupul de patru regiuni A'B'E conţine două perechi de câte două regiuni aflate de fiecare parte a liniei de reflexie. Acelaşi lucru este valabil şi pentru grupul format din două regiuni AB'DE. Aceste grupuri se formează prin reflexie. Atunci când folosim acest stil de hartă Karnaugh, va trebui să căutăm astfel de grupuri reflectate. Expresia booleană simplificată mai sus este următoarea:

ieşire = A'B'E  +
         B'C'E  +
         A'C'DE +
         A'CD'E +
         ABCE   +
         AB'DE  +
         A'B'C'D

Să considerăm şi varianta hărţii Karnaugh cu 5 variabile, cu suprapunere:

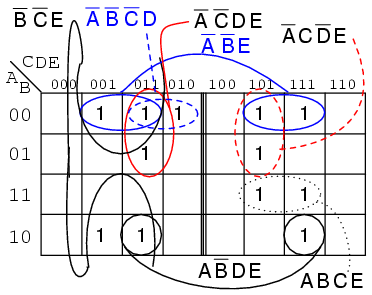
Dacă facem o coparaţie între cele două variante de sus, anumite regiuni din partea dreaptă a hărţii îşi modifică locatie, din moment ce adresele din partea de sus a hărţii s-au modificat. Trebuie de asemenea să găsim o altă modalitate de grupare a termenilor din cele două jumătăţii ale hărţii. Soluţia constă în suprapunerea (imaginară) a celor două jumătăţi. Orice suprapunere a hărţii de deasupra cu harta de dedesupt prezintă o posibilă grupare. Figura de mai jos indică faptul că grupul AB'DE este compus din două regiuni suprapuse. Grupul A'B'E este format din două perechi de regiuni suprapuse:

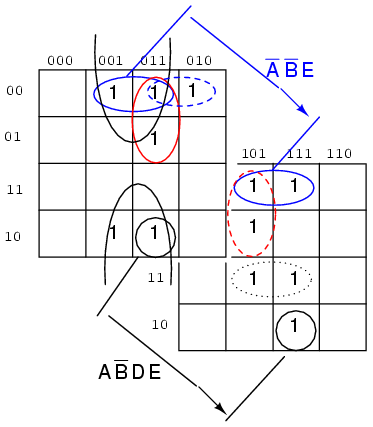
Pentru grupul A'B'E de patru regiuni, ABCDE = 00xx1. Cu alte cuvinte, variabilele A, B şi E sunt aceleaşi (001) pentru grup. Pe de altă parte, CD = xx (acesta variabile nu sunt identice pentru grup). Din moment ce ABCDE = 00xx1, grupul de patru regiuni este acoperit de A'B'XXE = A'B'E.

8.10.2 Hartă Karnaugh de 6 variabile

Luăm acum un exemplu de utilizare a unei hărţi Karnaugh de 6 variabile. Am suprapus (imaginar) cele patru sub-hărţi pentru a putea vizualiza gruparea de patru regiuni corespunzătoare ieşirii C'F':

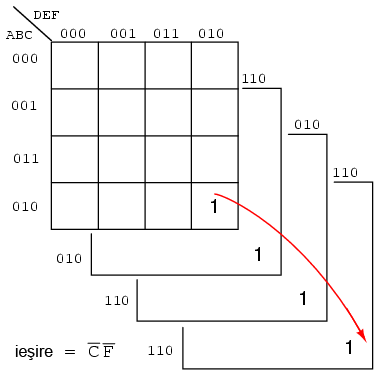
Un comparator de amplitudine (utilizat pentru ilustrarea utilizării hărţii Karnaugh de 6 variabile) compară două numere binare. Acesta indică dacă cele două numere sunt egale, mai mici sau mai mari unul faţă de celălalt. Un astfel de comparator are trei ieşiri:

Un comparator de amplitudine pe trei biţi are două intrări: A₂A₁A₀ şi B₂B₁B₀. Un comparator de amplitudine sub forma unui circuit integrat (7485) are practic patru intrări. Totuşi, harta Karnaugh de mai jos trebuie menţinută la o mărime rezonabilă. Vom rezolva problema doar pentru ieşirea A>B.

Pentru simplificarea logicii comparatorului de amplitudine pe 3 biţi, folosim harta Karnaugh cu 6 variabile de mai jos. Această variantă este cea cu suprapunere. Codul binar folosit nu este cod Gray. Găsim expresiile redundante prin suprapunerea celor patru sub-hărţi, precum am arătat mai sus. Am putea găsi regiuni comune tuturor celor patru hărţi, deşi, în exemplul de mai jos nu este cazul. Putem observa totuşi că există regiuni comune sub-hărţilor:

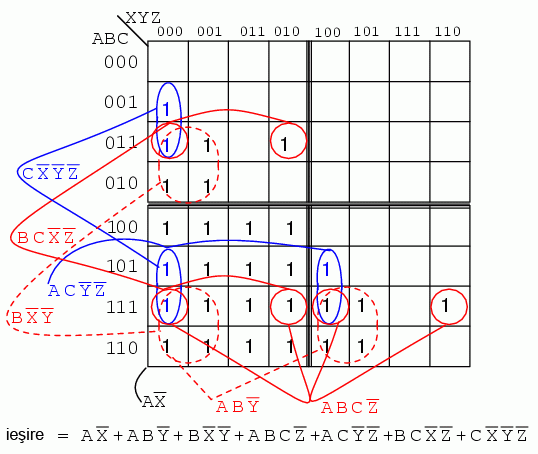
Ieşirea A>B este reprezentată de ABC>XYZ pe harta de mai sus. Ori de căte ori ABC este mai mare decât XYZ, avem o valoare de 1 pe hartă. Pe prima linie, ABC = 000 nu poate fi mai mare decât nicio valoare a lui XYZ. Nu avem nici o valoare de 1 pe această linie. Pe linia a doua, ABC = 001, şi doar în prima regiune, ABCXYZ = 001000, ABC este mai mare decât XYZ. Avem un un singur 1 în prima regiune a celei de a doua linii. Pe linia a patra, ABC = 010, există o pereche de 1. Pe linia a treia, ABC = 011 şi avem trei valori de 1. Prin urmare, harta este completată cu valori de unu ori de câte ori ABC este mai mare decât XYZ.

Pentru gruparea regiunilor, acolo unde este posibil, încercăm să formăm grupuri cu sub-harţile adiacente. Toate grupurile în afară de un grup de 16 regiuni sunt formate cu regiuni aparţinând sub-hărţilor adiacente. Rezultatul este: 1 grup de 16 regiuni; 2 grupuri de 8 regiuni; 4 grupuri de 4 regiuni. Grupul de 16 regiuni, AX', ocupă toată sub-harta din partea de jos-stânga a hărţii Karnaugh, deşi, în figura de mai sus, aceasta nu este încercuită.

Numărând valorile de 1 de pe hartă, ajungem la un total de 16 + 6 + 6 = ...

Înainte de reducerea logică folosind harta Karnaugh de mai sus, soluţia logică sub formă de sumă de produse ar fi avut 28 de termeni, fiecare cu 6 intrări. Simplificarea logică cu ajutorul hărţii Karnaugh de mai sus, a redus numărul termenilor la şapte, fiecare cu un număr de patru sau mai puţin de patru intrări. Acesta este de fapt scopul hărţilor Karnaugh!