< Exemple practice

2 Circuite de curent continuu

2.1 Conectarea bateriilor în serie

2.1.1 Scopul experimentului

Vom vedea mai jos modul de conectare a bateriilor pentru a obţine diferite valori ale tensiunii rezultate. Deşi putem folosi baterii de orice mărime, este recomandat să aveţi cel puţin două baterii cu valori ale tensiunii diferite, pentru a face experimentul mai interesant.

Pe parcurs, vom realiza circuitul de mai jos (schemă + circuit practic):

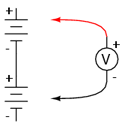
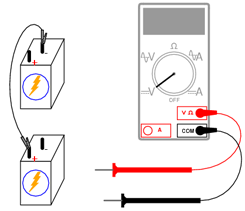
2.1.2 Desfăşurarea experimentului

Conectarea componentelor în serie înseamnă conectarea lor în linie, astfel încât să existe un singur drum pe care să poată circula electronii. Conectaţi aşadar două baterii electrice în serie. Borna pozitivă a unei baterii trebuie să fie conectată la borna negativă a celeilalte. Măsuraţi căderea de tensiune la bornele fiecărei baterii, cu ajutorul unui voltmetru. Măsuraţi apoi căderea de tensiune la bornele celor două baterii conectate în serie. Veţi observa că cele două valori ale tensiunii se adună:

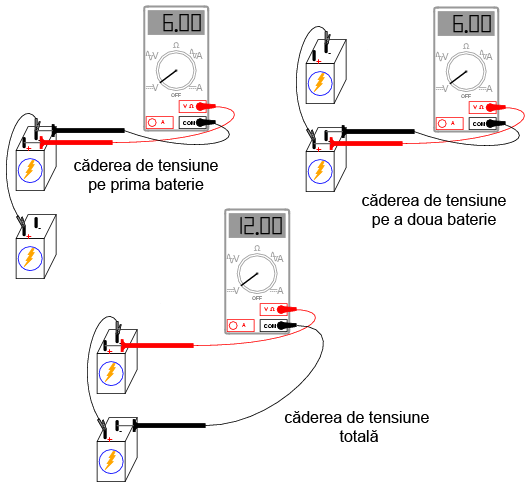
Încercaţi să conectaţi baterii de tensiuni diferite în serie. De exemplu, conectaţi o baterie de 6 V cu una de 9 V. Care este valoarea totală a tensiunii în acest caz?

Inversaţi apoi conexiunile celor două baterii, conectând borna negativă(-) a uneia dintre baterii cu borna negativă(-) a celeilalte. Pe scurt, conectaţi-le în contra-serie, astfel:

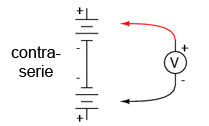
Care este valoarea tensiunii în acest caz. Care este diferenţa faţă de cazul precedent? Puteţi deduce polaritatea căderii de tensiune, cunoscând polarităţile individuale ale bateriilor şi valorile tensiunilor lor?

2.2 Conectarea bateriilor în paralel

2.2.1 Scopul experimentului

Vom realiza circuitele de mai jos (schema teoretică şi circuitul practic), şi vom observa efectul conectării surselor de putere în paralel asupra tensiunii şi a curentului din circuit:

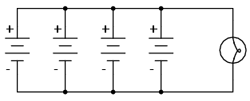
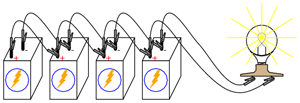
2.2.2 Derularea experimentului

Conectaţi o baterie de 6 V la un bec de 12 V, cu o putere de 25 sau 50 W. Becul va lumina relativ slab în acest caz. Utilizaţi voltmetrul pentru determinarea căderii de tensiune la bornele becului, astfel:

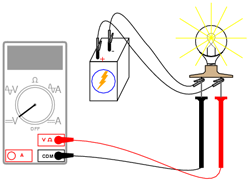
Indicaţia voltmetrului ar trebui să fie mai mică decât tensiunea normală a bateriei. Dacă veţi folosi voltmetrul pentru citirea căderii de tensiune direct la bornele bateriei, veţi observa că şi în acest caz tensiunea este mai mică. De ce se întâplă acest lucru? Valoarea mare a curentului absorbit de bec (putere înaltă) duce la scăderea tensiunii la bornele bateriei. Acest lucru se datorează căderii de tensiune dezvoltate la bornele rezistenţei interne a bateriei.

Putem rezolva această problemă prin conectarea bateriilor în paralel. Astfel, fiecare baterie va fi nevoită să susţină doar o fracţiune din curentul total necesar becului. Conexiunile paralel presupun conectarea tuturor terminalelor pozitive (+) ale bateriilor între ele (terminale electric comune). Acelaşi lucru este valabil şi în cazul terminalelor negative (-).

Adăugaţi pe rând bateriile în paralel, observând tensiunea becului cu fiecare nouă baterie:

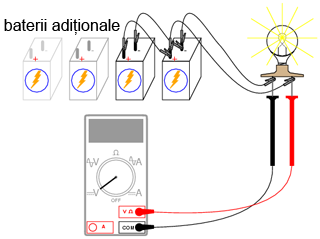
De asemenea, intensitatea luminii becului ar trebui să crească cu fiecare nouă baterie adăugată în paralel. Încercaţi să măsuraţi curentul unei baterii. Comparaţi această valoare cu valoarea curentului total (prin bec). Cea mai uşoară metodă de măsurare a curentului unei singure baterii, este următoarea:

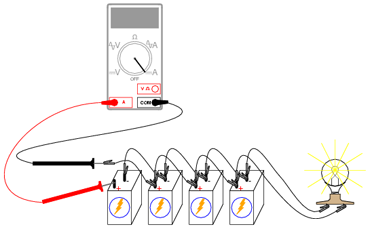
Întrerupem circuitul pentru o singură baterie. Introducem apoi ampermetrul în locul întreruperii, astfel încât circuitul este acum închis, şi putem măsura curentul prin bateria respectivă. Măsurarea curentului total este similară: deschidem circuitul într-un loc prin care circulă curentul total şi conectăm ampermatrul între cei doi conductori liberi:

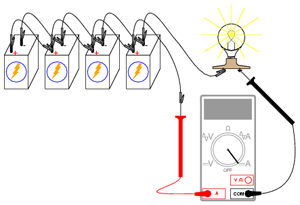
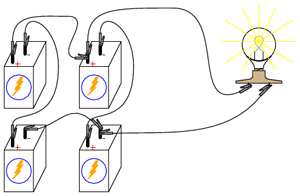
Observaţi diferenţa dintre curentul unei singure baterii şi curentul total. Pentru a obţinea cea mai mare iluminare, avem nevoie însă de o conexiune serie-paralel. Două baterii de 6 V conectate în serie vor genera o tensiune de 12 V. Conectăm apoi două astfel de combinaţii serie în parale. O astfel de combinaţie poate susţine mult mai uşor valoarea curentului necesară alimentării becului. Tensiunea pe fiecare baterie va fi în acest caz mult mai aproape de 6 V:

2.3 Divizor de tensiune

2.3.1 Scopul experimentului

Pentru derularea acestui experiment veţi avea nevoie de diferiţi rezistori cu valori între 1 kΩ şi 100 kΩ. Altfel, s-ar putea să nu obţineţi valori corecte ale tensiunii şi curentului măsurat cu ajutorul multimetrului. În cazul unor rezistenţe mici, rezistenţa internă a ampermetrului are un impact destul de mare asupra acurateţii măsurătorii. Rezistenţele foarte mari pot cauza probleme măsurătorilor de tensiune. Rezistenţa internă a voltmetrului în acest caz modifică rezistenţa circuitului când acesta este conectat în paralel cu un rezistor de valoare mare.

În urma realizării acetui experiment, vă veţi familiariza cu utilizarea legii lui Kirchhoff pentru tensiune, precum şi cu realizarea unui divizor de tensiune. Vom realiza circuitul de mai jos (diagrama):

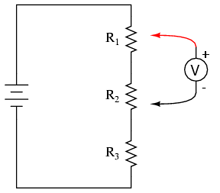
Practic, acest poate fi realizat în oricare din formele de mai jos (care va este mai la îndemână):

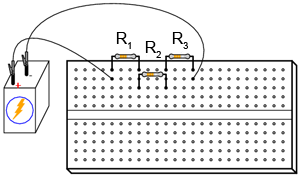
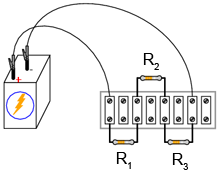
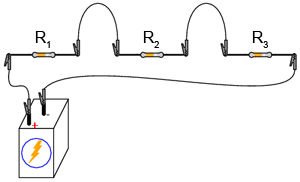
Alternativ, puteţi încerca realizarea tuturor celor trei variante de mai sus. Vă veţi familiariza astfel cu toate cele trei metode. Fiecare are avantajele şi dezavantajele sale. Ultima variantă - în care toate componentele sunt conectate între ele folosind conductori cu crocodili - este cea mai neprofesională, dar perfectă pentru un experiment precum cel de faţă. Construcţia circuitului pe placa de test este cea mai versatilă. Placa de test permite o densitate mare de componente (multe componente pe o suprafaţă mică), dar circuitului este temporar. Regleta de borne oferă un circuit mult mai permanent, dar o densitatea mică de componente.

2.3.2 Desfăşurarea experimentului

Alegeţi trei rezistori şi măsuraţi valoarea rezistenţei fiecăruia cu un ohmmetru. Notaţi-vă aceste valori pentru utilizarea lor ulterioara.

Conectaţi cei trei rezistori în serie. Conectaţi apoi şi bateria, conform figurilor de mai sus. Măsuraţi tensiunea bateriei cu un voltmetru după ce aţi realizat circuitul. Notaţi-vă şi această valoare. Este indicat să măsuraţi tensiunea bateriei în timpul alimentării rezistorilor, deoarece această valoare s-ar putea să difere puţin faţă de tensiunea normală a bateriei. Acest circuit nu ar trebui să prezinte o sarcină suficient de mare (curentul necesar nu este destul de mare) pentru a cauza scăderea tensiunii bateriei. Totuşi, măsurarea tensiunii bateriei sub sarcină este indicată în orice situaţie, întrucât oferă valori de calcul mult mai realiste.

Aplicaţi legea lui Ohm (I = E / R) pentru a calcula curentul din circuit. Verificaţi această valoare calculata prin măsurarea curentului cu un ampermetru astfel (metoda este similară indiferent de varianta circuitului):

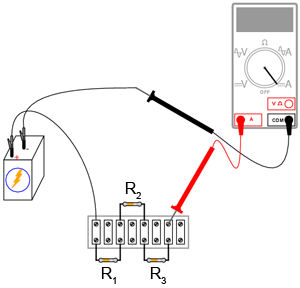
Dacă valorile rezistorilor pe care i-aţi ales se află într-adevăr în intervalul 1 kΩ - 100 kΩ, iar tensiunea bateriei este de aproximativ 6 V, valoarea curentului ar trebui să fie destul de mică (mA sau µA). Fiţi atenţi la prefixul afişat, într-unul din colţuri, în cazul multimetrelor digitale. Este foarte uşor să uităm aceste prefixe când citim valoarea măsurători.

Valoarea măsurată a curentului ar trebui să fie foarte apropiată de valoarea calculată folosind legea lui Ohm. Înmulţiţi acum valoarea calculată pentru curent cu valoarea rezistenţei fiecărui rezistor. Aflaţi astfel valoarea căderilor de tensiune (E = IR). Măsuraţi apoi cu ajutorul voltmetrului căderea de tensiune reală pe fiecare rezistor, verificând astfel acurateţea calculelor. Din nou, cele două valori, cea calculată şi cea măsurată, trebuie să fie extrem de apropiate.

2.3.3 Explicarea divizorului de tensiune

Fiecare cădere de tensiune a rezistorilor este doar o fracţiune din tensiunea totală. De aici şi denumirea de divizor de tensiune a acestui circuit. Această valoare subunitară este determinată de rezistenţa individuală a rezistorului şi de rezistenţa totală a circuitului.

Dacă tensiunea unui rezistor este de 50% din tensiunea totală a bateriei, acest procent va rămâne neschimbat atâta timp cât valorile rezistorilor nu se modifică, indiferent de tensiunea bateriei. Prin urmare, dacă tensiunea totală este de 6 V, tensiunea rezistorului respectiv va fi 50% din această valoare, adică 3 V. Dacă tensiunea totală este 20 V, căderea de tensiune la bornele rezistorului va fi de 10 V, sau 50% din 20 V.

2.3.4 Validarea legii lui Kirchhoff pentru tensiune

Identificaţi fiecare punct din circuit cu un număr. Punctele ce sunt electric comune trebuiesc notate cu acelaşi număr, astfel:

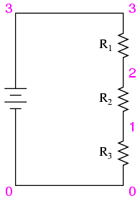
Practic, circuitul se poate realiza prin lipirea unei benzi adezive la capătul conductorilor pe care este scris numărul punctului respectiv de contact din circuit:

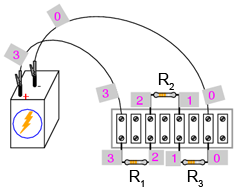
Folosiţi un voltmetru digital (acest lucru este important!). Măsuraţi căderile de tensiune în jurul buclei formate din punctele 0-1-2-3-0. Notaţi-vă fiecare din aceste tensiuni, cât şi semnul indicat de voltmetrul. Cu alte cuvinte, dacă valoarea afişată de voltmetru este -1,325 V, notaţi această valoare cu semnul minus. Nu inversaţi sondele voltmetrului pentru a obţine o citire „corectă” (pozitivă). Semnul matematic este foarte important pentru exemplificarea legii lui Kirchhoff. Paşii pe care trebuie sa-i urmaţii sunt următorii:

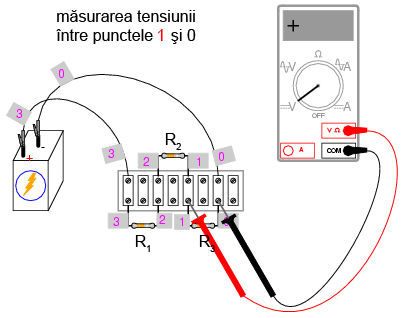
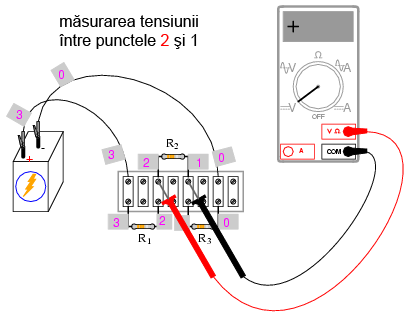
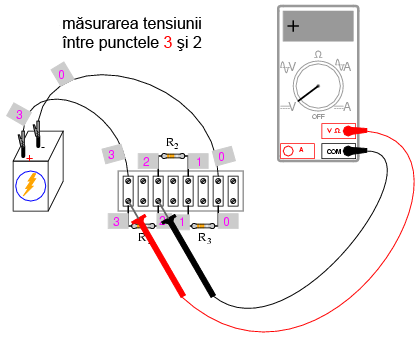
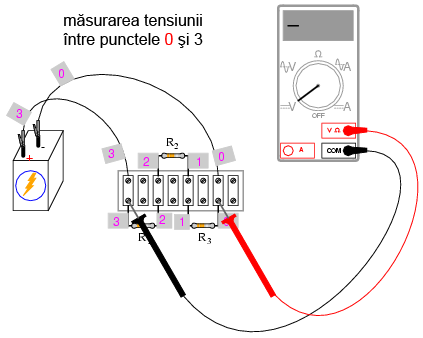
Folosind astfel voltmetrul pentru a „păşi” în jurul circuitului, veţi obţine trei tensiuni pozitive şi o tensiune negativă:

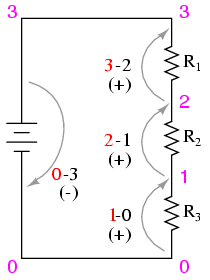
Adunaţi toate aceste valori algebric (respectând semnul). Rezultatul sumei trebuie să fie zero. Acesta este principiul fundamental al legii lui Kirchhoff pentru tensiune: suma algebrică a tutor căderilor de tensiune dintr-o buclă trebuie să fie egală cu zero.

Indiferent de sensul de parcugere al buclei, rezultatul este acelaşi. Încercaţi să realizaţi o buclă închisă între oricare seturi de puncte. Suma algebrică a căderilor de tensiune va fi tot timpul egală cu zero. Această lege este valabilă indiferent de configuraţia circuitului studiat: serie, paralel, serie-paralel sau circuit complex.

2.4 Divizor de curent

2.4.1 Scopul experimentului

Asemănător exemplului precedent, vom avea nevoie de o baterie de 6 V şi o serie de rezistori cu valori cuprinse între 1 kΩ şi 100 kΩ. Faţă de exemplul precedent, ne vom familiariza cu legea lui Kirchhoff pentru curent şi cu funcţionarea unui circuit divizor de curent.

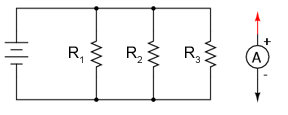
Circuitul se poate realiza practic în mai multe moduri:

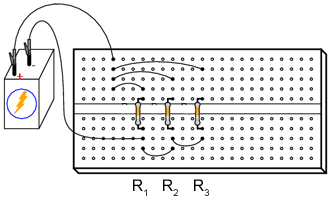
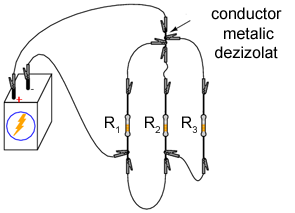
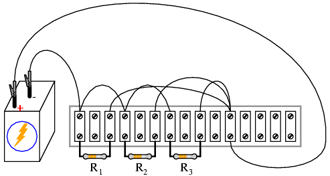
În mod normal, nu este recomandat să conectaţi mai mult de doi conductori sub acelaşi terminal (şurub). În exemplul de mai sus, există trei conductori conectaţi împreună la terminalul din dreapta sus. Am realizat acest lucru doar pentru a demonstra un concept (sumarea curentului la nodul unui circuit), şi nu reprezintă o tehnică profesională de realizare a circuitelor.

Experimentaţi cu toate cele trei variante de realizare a circuitului pentru a vă familiariza cu avantajele şi dezavantajele fiecăruia.

2.4.2 Desfăşurarea experimentului

Alegeţi trei rezistori şi măsuraţi valoarea rezistenţei fiecăruia dintre ei cu ajutorulu unui ohmmetru. Notaţi-vă valoarea acestora pe o hârtie. Conectaţi cei trei rezistori în paralel şi conectaţi apoi şi baterie, precum în figurile de mai sus. Măsuraţi tensiunea bateriei cu un voltmetru, după ce aţi conectat rezistorii la bornele acesteia. Notaţi-vă şi această valoare pe hârtie. Este indicat să măsuraţi tensiunea bateriei în timp ce este alimentată, deoarece valoarea măsurată s-ar putea să difere într-o mică măsura de valoarea normală (fără sarcină).

Măsuraţi tensiunea la bornele fiecărui rezistor. Ce observaţi? Într-un circuit serie, valoarea curentului este aceiaşi prin toate componentele în orice moment. Într-un circuit paralel, tensiunea este variabila comună a tuturor componentelor.

Aplicaţi legea lui Ohm (I = E / R) pentru a calcula curentul prin fiecare rezistor. Verificaţi apoi această valoare calculată măsurând curentul real cu ajutorul unui ampermetru, astfel: conectaţi sonda roşie a ampermetrului în punctul de întâlnire a bornelor pozitive (+) ale rezistorilor; conectaţi borna neagră, pe rând, la capătul celălalt (-) al rezistorilor. Observaţi atât atât valoarea cât şi polaritatea curentului. De exemplu, pentru a calcula curentul prin rezistorul R₁:

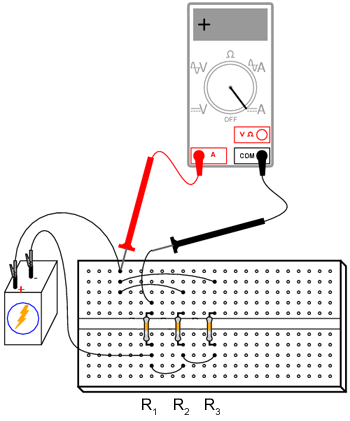
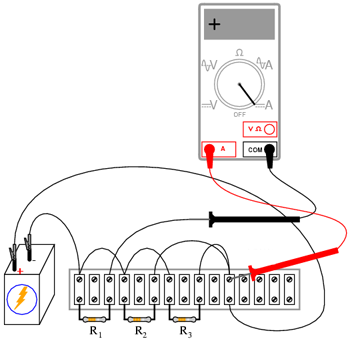
Măsuraţi curentul pentru toţi cei trei rezistori. Comparaţi aceste valori cu rezultatele obţinute anterior. Conectând ampermetrul asemenea figurilor de mai sus, toate cele trei indicaţii trebuie să fie pozitive, nu negative.

2.4.3 Validarea legii lui Kirchhoff pentru curent

Măsuraţi apoi curentul total din circuit, astfel: ţineţi sonda roşie a ampermetrului într-un singur punct din circuit; deconectaţi conductorul ce duce la borna pozitivă (+) a bateriei şi atingeţi-l cu sonda neagră.

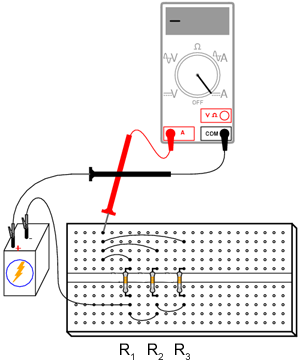
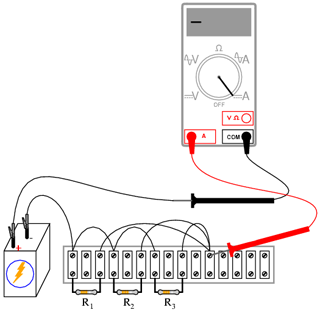
Notaţi-vă atât valoarea cât şi semnul curentului indicat de ampermetru. Faceţi suma algebrică dintre această valoare şi valorile curenţilor pentru cei trei rezistori. Ce observaţi similar legii lui Kirchhoff pentru tensiune? Legea lui Kirchhoff pentru curent spune că suma tuturor curenţilor dintr-un nod trebuie să fie egală cu zero. Această lege este foarte utilă în analiza matematică a circuitelor electrice.

2.4.4 Explicare divizorului de curent

Observaţi cele patru valori ale curenţilor obţinute din măsurători. Consideraţi-le pe toate ca şi valori pozitive. Primele trei reprezintă curentul prin fiecare rezistor. a patra valoare reprezintă curentul total prin circuit ca şi suma pozitivă a celor trei curenţi pe fiecare ramură. Fiecare curent de ramură este o fracţiune, sau un procent, din curentul total. Din acest motiv, acest tip de circuit (cu rezistori conectaţi în paralel) poartă numele de divizor de curent.

2.5 Divizor de tensiune cu potenţiometru

2.5.1 Scopul experimentului

Pentru derularea acestui experiment veţi avea nevoie de două baterii de 6 V, o mină de grafit (creion mecanic), un potenţimetru liniar cu o singură înfăşurare (5 kΩ - 50 kΩ) şi un potenţiometru liniar cu înfăşurări multiple (1 kΩ - 20 kΩ).

Vom experimenta aşadar cu modul de realizare şi de funcţionare a unui divizor de tensiune. Vom vedea, de asemenea, modul în care se însumează tensiunile în serie. Circuitul pe care îl vom realiza, este următorul (schema plus circuite implementate practic):

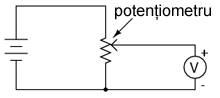
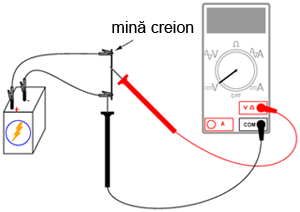
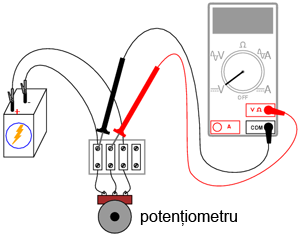
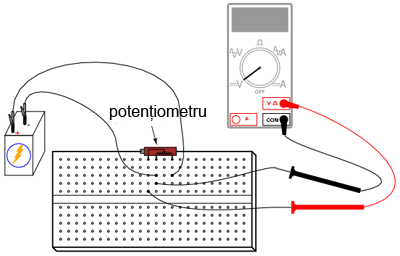
2.5.2 Desfăşurarea experimentului

Începeţi experimentul cu circuitul format din mina de creion. Grafitul din care este realizată mina este un conductor prost de curent electric. Acesta va juca prin urmare rolul unui rezistor conectat la bornele bateriei de 6 V prin intermediul crocodililor. Conectaţi voltmetrul precum în figură şi atingeţi cu sonda roşie mina de grafit. Deplasaţi sonda roşie în lungul minei şi observaţi indicaţia voltmetrului. Care este poziţia sondei pentru care indicaţia voltmetrului este maximă?

Practic, mina de grafit se comportă precum o pereche de rezistori. Raportul dintre cele două rezistenţe este stabilit de poziţia sondei roşii pe lungimea acestuia:

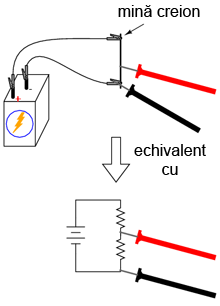
Modificaţi apoi poziţia sondelor voltmetrului, astfel încât să măsuraţi tensiunea pe „rezistorul de sus” a minei, astfel:

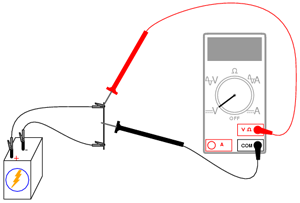
Repoziţionaţi sonda neagră pe lungimea minei şi observaţi indicaţia voltmetrului. Care este poziţia pentru care tensiunea indicată de voltmetru este maximă? Există vreo diferenţă între această situaţie şi cea precedentă? De ce?

2.5.3 Circuitul cu potenţiometru

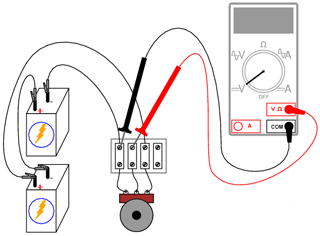
Realizaţi circuitul cu potenţiometru prezentat la începutul capitolului, în locul celui cu mină de creion. Măsuraţi tensiunea bateriei în timp ce potenţiometrul este alimentat. Notaţi-vă această valoare pe o hârtie. Măsuraţi tensiunea dintre perie şi capătul potenţiometrului conectat la borna negativă (-) a bateriei. Ajustaţi mecanismul potenţiometrului până când voltmetrul indică exact 1/3 din tensiunea totală. Pentru o baterie de 6 V, această valoare va fi de aproximativ 2 V.

Conectaţi apoi două baterii în serie, pentru a obţine o tensiune de 12 V pe potenţiometru. Măsuraţi tensiunea totală a bateriei şi măsuraţi apoi tensiunea între aceleaşi două puncte pe potenţiometru (între perie şi borna negativă). Împărţiţi tensiunea măsurată pe potenţiometru cu tensiunea totală măsurată pe baterie. Rezultatul ar trebui să fie 1/3, aceiaşi valoare a divizorului de tensiune ce am găsit-o şi înainte:

2.6 Potenţiometrul ca şi reostat

2.6.1 Scopul experimentului

Vom avea nevoie de o baterie de 6 V, un potenţiometru liniar cu o singură înfăşurare (5 kΩ) şi un motor electric mic cu magneţi permanenţi. Vom învăţă în acest experiment cum să utilizăm un reostat, cum să folosim un potenţiometru pe post de reostat, cum putem controla viteza de rotaţie a unui motor şi cum putem folosi un voltmetru pentru a verifica continuitatea circuitului în locul ampermetrului.

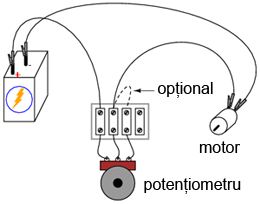
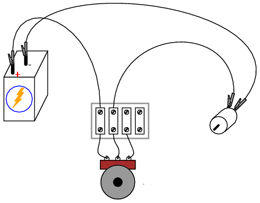
Pe parcursul experimentului vom realiza circuitul de mai jos (diagramă plus implementare practică):

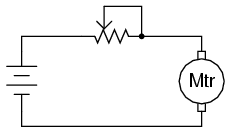
2.6.2 Realizarea reostatului din potenţiometru

Potenţiometrele se utilizează de obicei pe post de divizori de tensiune, poziţia periei determinând raportul de divizare. Totuşi, există aplicaţii în care nu avem nevoie de un divizor de tensiune variabil, ci doar un rezistor variabil: un dispozitiv cu două terminale. Tehnic, un rezistor variabil este cunoscut sub numele de reostat, dar potenţiometrele pot fi utilizate foarte bine pe post de reostat.

În cea mai simplă comfiguraţie, potenţiometrul poate fi folosit pe post de reostat prin simpla utilizare a doi dintre terminalii acestuia. Cel de al treilea terminal este lăsat neconectat şi neutilizat:

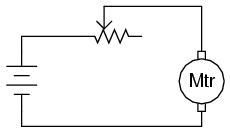
Deplasarea periei potenţiometrului astfel încât aceasta să se apropie de celălalt terminal utilizat rezultă în descreşterea rezistenţei. Direcţia necesară creşterii sau descreşterii rezistenţei poate fi schimbată prin utilizarea unor seturi diferite de terminali:

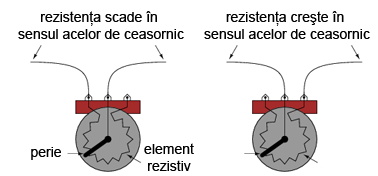
Fiţi atenţi însă să nu folosiţi cei doi terminali externi. Acest lucru nu va duce la modificarea rezistenţei atunci când poziţia periei se schimbă. Cu alte cuvinte, potenţiometrul nu va mai funcţiona ca şi o rezistenţă variabilă:

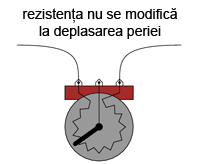
2.6.3 Controlul vitezei motorului

Realizaţi circuitul prezentat la început, utilizând doar doi terminali ai potenţiometrului. Observaţi modul în care poate fi controlată viteza motorului prin ajustarea poziţiei periei potenţiometrului. Experimentaţi cu diferite conexiuni ale terminalilor. Observaţi comportamentul motorului. Dacă potenţiometrul vostru are o rezistenţă mare (măsurată între cei doi terminali externi), s-ar putea ca motorul să nu se rotească deloc până în momentul în care peria este adusă foarte aproape de terminalul extern conectat (rezistenţa mică).

După cum puteţi observa, viteza motorului poate fi variată folosind un reostat conectat în serie cu acesta. Reostatul modifică rezistenţa totală a circuitului şi limitează curentul total. Această metodă de control este însă ineficientă, deoarece puterea disipată (pierdută) de reostat este destul de mare. O metodă mult mai eficientă constă în alimentarea motorului cu o putere pulsatorie, folosind un tranzistor. O metodă similară este folosită şi în cazul dimmer-elor casnice.

2.6.4 Conectarea terminalului liber la terminalul-perie (opţional)

Când folosim potenţiometrul pe post de reostat, adesea, terminalul nefolosit este conectat la terminalul perie, astfel:

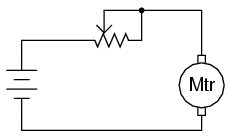
Într-o primă instanţă, acest lucru pare complet inutil, întrucât nu are niciun impact asupra controlului rezistenţei. Puteţi verifica acest lucru prin introducerea unui nou fir în circuitul realizat. Comparati comportamentul motorului înainte şi după această modificare:

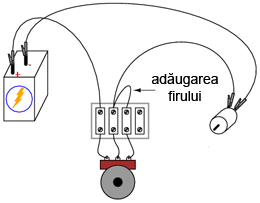
Dacă potenţiometrul este în stare bună de funcţionare, acest conductor adiţional nu are niciun efect asupra funcţionării motorului. Totuşi, dacă peria pierde contactul cu elementul rezistiv din interiorul potenţiometrului, această conexiune adiţională menţine circuitul închis. În unele aplicaţii, acest lucru poate fi important.

Puteţi simula un asemenea „defect” a contactului periei. Deconectaţi terminalul din mijloc al potenţiometrului din circuit. Măsuraţi tensiunea motorului pentru a vă asigura că acesta este încă alimentat:

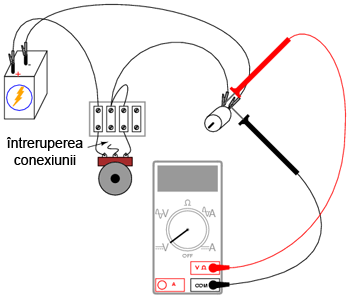
2.6.5 Verificarea circuitelor cu voltmetrul în locui ampermetrului

Ar fi trebuit să măsuraţi curentul din circuit în loc de tensiunea motorului pentru a verifica continuitatea circuitului (circuit închis). Totuşi, această metodă este mult mai sigură deoarece nu implica deschiderea circuitului pentru conectarea în serie a ampermetrului. Ori de câte ori folosim un ampermetru, există riscul unui scurt-circuit prin conectarea acestuia la bornele unei surse substanţiale de tensiune. Rezultatul poate fi distrugerea aparatului de măsură sau chiar accidentarea persoanei respective.

Nu este şi cazul voltmetrelor însă. Prin urmare, ori de câte ori puteţi la fel de bine măsura tensiunea în detrimentul măsurării curentului (utilizarea voltmetrului în detrimentul ampermetrului), pentru a verifica exact acelaşi lucru, varianta tensiunii este cea indicată.

2.7 Termoelectricitate

2.7.1 Scopul experimentului

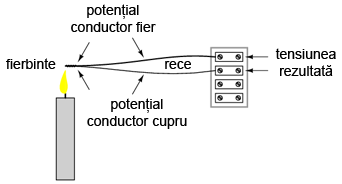
Vom vedea pe parcursul acestui experiment modul de funcţionare şi utilizare a unei termocuple. Veţi avea nevoie de un conductor de cupru şi unul de fier (eventual de aluminiu), ambele dezizolate, o lumânare şi bucăţi de gheaţă. Circuitul electric pe care îl vom realiza este cel de jos:

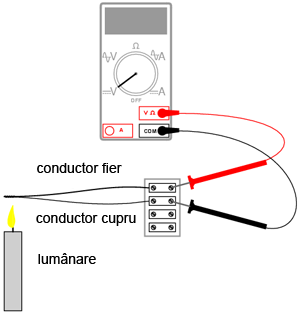
2.7.2 Realizarea termocuplei

Răsuciţi un capăt al conductorului de fier cu un capăt al conductorului de cupru. Conectaţi celelalte capete rămase libere la o bornă de reglete. Setaţi voltmetrul pe cea mai sensibilă scară şi conectaţi-l la borna de regletă, conform figurii de mai sus. Indicaţia voltmetrului ar trebui să fie aproximativ 0 V.

Ceea ce am construit mai sus poartă numele de termocuplă: un dispozitiv folosit pentru generarea unei căderi de tensiune mici. Tensiunea produsă este proporţională cu diferenţa de temperatură dintre punctul de contact al celor doi conductori şi punctul de contact al voltmetrului cu cele două capete rămase libere. Dacă temperatura contactului este egală cu temperatură capetelor libere, tensiunea produsă va fi 0 V. Indicaţia voltmetrului indică exact acest lucru.

2.7.3 Generarea tensiunii cu ajutorul termocuplei create

Aprindeţi o lumânare şi puneţi contactul (vârful) termocuplei în flacără. Observaţi indicaţia voltmetrului. Îndepărtaţi contactul termocuplei din flacără şi lăsaţi-l să se răcească până când indicaţia voltmetrului se apropie din nou de zero.

Atingeti apoi contactul termocuplei cu un cub de gheaţă şi observaţi indicaţia voltmetrului. Ce puteţi spune despre valoare tensiunii generate, este mai mică sau mai mare decât în cazul precedent? Care este diferenţa dintre polaritatea tensinilor generate în cele două cazuri?

După ce aţi îndepărtat cubul de gheaţă, încălziţi contactul termocuplei ţinându-l între degete. Va dura puţin până când temperatura acestuia va atinge temperatura corpului vostru. Aveţi răbdare însă şi observaţi îndicaţia voltmetrului.

Termocuplele sunt folosite pe post de dispozitive de măsurare a temperaturii. Ralaţia matematică dintre diferenţa temperaturii şi tensiunea rezultată este destul de liniară. Prin măsurarea tensiunii, putem determina temperatura la punctul de contact.

2.8 Circuit de mediere

2.8.1 Scopul experimentului

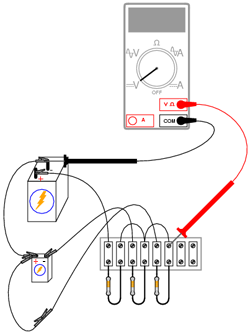
Vom vedea în cele ce urmează cum puem realiza media aritmedică a valorilor tensiunilor cu ajutorul unei reţele de rezistori. Aceasta este de fapt o aplicaţie a teoremei lui Millman. Veţi avea nevoie de 3 baterii (sau surse de alimentare în c.c.), fiecare cu o tensiune diferită şi trei rezistori cu rezistenţe egale (între 10 kΩ şi 47 kΩ fiecare). Practic, vom realiza circuitul de mai jos:

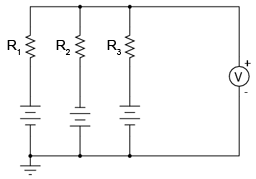
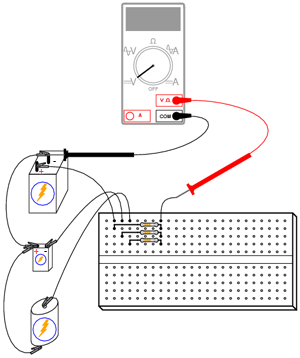
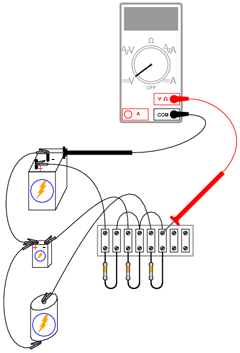
Acest circuit realizează funcţia matematică de mediere. Practic, intrarea circuitului constă din cele trei tensiuni, iar ieşirea din media aritmetică a acestora, astfel:

Vieşire = (V1 + V2 + V3) / 3

2.8.2 Realizarea şi funţionarea circuitului de mediere

Construiţi acest circuit conform figurii de mai sus. Măsuraţi apoi tensiunile celor trei baterii cu ajutorul unui voltmetru. Notaţi-vă aceste valori pe o foaie de hârtie şi calculaţi media lor aritmetică, conform formulei de mai sus. Când măsuraţi tensiunea fiecărei baterii, ţineţi sonda neagră conectată la „masă” (partea bateriei conectată direct la celelalte baterii prin conductorii de legătură). Atingeţi celălalt terminal al bateriei cu sonda roşie. Polaritatea este foarte importantă în această situaţie. Puteţi observa din schema de mai sus, că una din baterii este conectată invers faţă de celelalte două. Tensiunea acestei baterii va trebui să fie negativă atunci când o măsurăm cu un voltmetru digital. Tensiunile celorlalte două baterii vor fi pozitive.

Când voltmetrul este conectat în circuit conform figurii de mai sus, valoarea indicată (V_ieşire) va fi media aritmetică a tensiunilor celor trei baterii. Dacă valorile rezistorilor sunt astfel alese încât să fie foarte apropiate între ele, tensiunea de ieşire a circuitului va fi foarte aproape de valoarea calculată pe hârtie.

Dacă una dintre baterii este deconectată, valoarea tensiunii de ieşire va fi egală cu media aritmetică a celor două tensiuni rămase (baterii). În cazul în care conductorii de legătură conectaţi iniţial la bornele bateriei înlăturate din circuit, sunt conectaţi împreună, circuitul va realia media aritmetică a celor două tensiuni rămase împreună cu valoarea de 0 V. Tensiunea de ieşire va fi prin urmare mai mică:

2.8.3 Concluzii şi notă istorică

Datorită simplităţii acestui circuit, nu-l putem numi un „calculator” în adevăratul sens al cuvântului. Totuşi, acesta realizează foarte funcţia matematică de mediere, şi o realizează mult mai rapid decât sunt capabile calculatoarele digitale. Acestea din urmă realizează operaţiile matematice printr-o succesiune de paşi discreti. Calculatoarele analogice (precum cel de mai sus), realizează calculele într-un mod continuu, valorificând legea lui Ohm şi legile lui Kirchhoff în scop aritmetic. Calcularea răspunsului depinde de viteza de propagare a tensiunii prin întreg circuitul, practic, viteza luminii (aproximativ)!

Prin introducerea circuitelor de amplificare, semnalele de tensiune din reţelele analogice de calculatoare pot fi amplificate şi re-utilizate în alte reţele pentru a realiza o varietate de funcţii matematice. Astfel de calculatoare analogice sunt excelente pentru realizarea funcţiilor de integrare şi diferenţiere. Ele pot fi folosite prin urmare pentru simularea comportamentului unor sisteme mecanice, electrice şi chiar chimice destul de complexe.

La un moment dat, calculatoarele analogice erau considerate instrumentul cel mai important pentru cercetările din domeniul ingineriei. Pe parcurs însă, acestea au fost înlocuite de calculatoarele digitale, ce realizează operaţiile matematice cu o precizie mai bună decât cele analogice, chiar dacă viteza teoretică este mult mai mică. Cu toate acestea, realizarea practică a unor astfel de circuite, pentru începători, duce la o înţelegerea mult mai bună a funcţionării circuitelor electrice în general. Ce alte operaţii matematice credeţi că pot fi realizate cu astfel de circuite analogice?

2.9 Baterie din cartof

2.9.1 Scopul experimentului

Ne propunem să realizăm o baterie din cartof. Deşi acest experiment foloseşte cartoful pe post de baterie, puteţi folosi o varietate de fructe şi legume pe post de potenţiale baterii. Veţi avea nevoie prin urmare, pe lângă cartof (sau lămâie, de exemplu), de o bucată de zinc sau de metal galvanizat şi un conductor de cupru. Pentru electrodul de zinc, puteţi folos un cui galvanizat. Vom vedea importanţa reacţiilor chimice în funcţionarea bateriilor precum şi modul în care suprafaţa electrozilor influenţează funcţionarea bateriei. Ciurcuitul realizat este următorul:

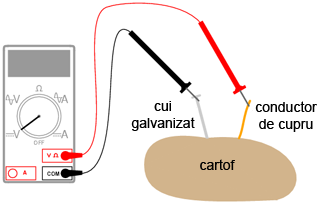
2.9.2 Realizarea bateriei din cartof

Introduceţi atât cuiul cât şi conductorul de cupru în cartof. Măsuraţi tensiunea produsă de baterie cu un voltmetru. Asta e tot!

Experimentaţi însă cu diferite metale, diferite adâncimi şi distanţe între electrozi. Cum puteţi obţine cea mai mare tensiune posibilă cu ajutorul cartofului? Încercaţi alte legume şi comparaţi tensiunile de ieşire pentru metale similare pe post de electrozi.

Desigur, alimentarea unei sarcini cu o astfel de „baterie” este foarte dificilă. Nu vă asteptaţi aşadar să alimentaţi un bec, un motor sau orice altceva. Chiar dacă tensiunea de ieşire este suficient de bună, rezistenţa internă a bateriei este destul de mare. Conectând mai mulţi cartofi în configuraţii serie, paralel sau serie-paralel, putem obţine o tensiune şi un curent destul de mare pentru alimentarea unei sarcini mici. Puteţi realiza acest lucru?

2.10 Încărcarea şi descărcarea condensatorului

2.10.1 Scopul experimentului

Vom observa modul de încărcare şi descărcare al condensatoarelor. Vom calcula constanta de timp a circuitului şi capacitatea rezultată prin conectarea condensatoarelor în serie şi paralel.

2.10.2 Materiale necesare

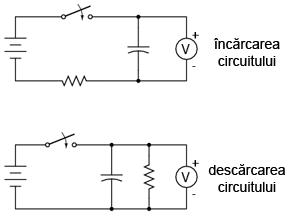
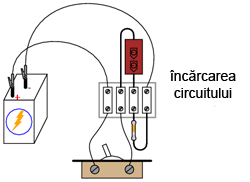
Pentru acest experiment veţi avea nevoie de o baterie de 6 V (sau sursă de tensiune echivalentă), două condensatoare electrolitice mari, de cel puţin 1000 µF, doi rezistori de 1 kΩ şi de un întrerupător. Circuitul realizat arată astfel:

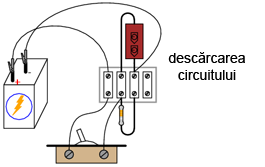
2.10.3 Atenţie la condensatoarele electrolitice

Acest experiment necesită utilizarea unor condensatoare mari pentru producerea unor constante de timp adecvate. Altfel, nu am putea urmări comportamentul circuitului cu ajutorul unui voltmetru şi a unui cronometru. Atenţie însă, majoritatea condensatoarelor de o asemenea capacitate sunt condensatoarele electrolitice. Polaritatea acestora este importantă! Cel puţin unul din terminalele fiecărui condensator este de obicei marcat cu polaritatea respecitvă. De obicei, pentru astfel de mărimi, condensatoarele sunt marcate printr-unul sau mai multe minusuri (-) pe partea terminalului negativ.

Dacă nu respectaţi indicaţia polarităţii, şi prin urmare, modul corect de alimentare al lor, mai mult ca sigur că aceste condensatoare se vor deteriora, chiar şi în cazul unei tensiuni mici de 6 V. Distrugerea condensatoarelor electrolitice constă de obicei în explozia lor şi împrăştierea materialelor chimice din interior. Încercaţi să evitaţi acest lucru !

2.10.4 Realizarea circuitului şi măsurarea constantei de timp

Construiţi circuitul de încărcare a condensatorului, precum în figura de mai sus. Măsuraţi tensiunea la terminalele condensatorului atunci când întrerupătorul este închis. Observaţi cum tensiunea creşte încet, cu timpul, şi nu brusc cum se întâmplă în cazul unui rezistor. Puteţi „reseta” condensatorul înapoi la tensiunea de 0 V prin scurt-circuitarea terminalelor acestuia pe o sarcină (rezistor, de exemplu).

Constanta de timp (τ) a unui circuit rezistor-condensator se calculează prin înmulţirea capacităţii şi a rezistenţei circuitului. Pentru un rezistor de 1 kΩ şi un condensator de 1.000 µF, constanta de timp ar trebui să fie 1 secundă. Aceasta este durata de timp pentru care tensiunea condensatorului creşte de la 0 V la aproximativ 63,2% din tensiunea sa finală: tensiunea bateriei.

Ar fi interesant de realizat un grafic, în care să vedem tensiunea condensatorului cu timpul. Pentru a putea realiza acest grafic totuşi, trebuie să găsim o metodă de încetinire a circuitului. O fereastră de o secundă nu este chiar suficientă pentru a putea măsura tensiuni cu un voltmetru.

Cum putem însă creşte constanta de timp a circuitului. Dacă ne uităm la formulă, există doar două posibilităţi: modificăm rezistenţa totală din circuit sau/si modificăm capacitatea totală a circuitului. Experimentaţi cu diferite combinaţi serie şi parelel, având la dispoziţie o pereche de rezistori identici şi o pereche de condensatori identici. Găsiţi combinaţia pentru care timpul de încărcare este cel mai lung.

Desigur, conectarea rezistorilor în serie formează o rezistenţă şi mai mare. Este valabil acest lucru şi în cazul condensatoarelor? Realizând acest circuit, vă puteti lămuri ce se întâmplă cu capacitatea condensatoarelor conectate în serie, respectiv paralel. Asiguraţi-vă însă de conectarea corectă a condensatoarele în circuit!

Circuitul de descărcare este similar celui de încărcare. Singura deosebire este că de această dată, tensiunea este maximă la închiderea întrerupătorului şi scade treptat după deschiderea acestuia. Experimentaţi şi în acest caz cu diferite combinaţii de rezistori şi condensatoare.

2.11 Circuit de diferenţiere

2.11.1 Scopul experimentului

Experimentul indică modul de realizare a unui circuit de diferenţiere. După realizarea circuitului, veţi putea obţine o înţelegere emipirică a derivatei unei funcţii.

2.11.2 Materiale necesare

Pentru realizarea circuitului veţi avea nevoie de două baterii de 6 volţi, un condensator de 0,1 µF, un rezistor de 1 MΩ şi un potenţiometru liniar, simplu, de 5 kΩ. Valoarea potenţiometrului nu este neapărat critică. Totuşi, teoretic, o valoare mai mică a rezistenţei potenţiometrului conduce la rezultate mai bune în acest experiment. Circuitul final arată astfel:

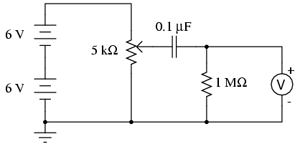
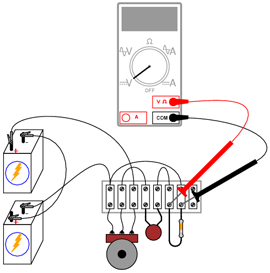
2.11.3 Realizarea circuitului

Măsuraţi tensiune dintre peria potenţiometrului şi punctul de masă reprezentat în figura de mai sus (terminalul negativ al bateriei de 6 V din partea de jos). Aceasta este tensiunea de intrare a circuitului. Puteţi observa cum această tensiune variază continuu între 0 şi 12 V pe măsură ce deplasăm peria potenţiometrului. Din moment ce utilizăm potenţiometrul pe post de divizor de tensiune, acest comportament ar trebui să vă fie deja cunoscut.

Măsuraţi apoi tensiunea la bornele rezistorului de 1 MΩ pe măsură ce învârţiţi potenţiometrul. Setaţi voltmetrul pe cea mai sensibiliă (mV) scară. Ce indică voltmetrul atunci când nu învârtim controlul potenţiometrului? Învârtiţi potenţiometrul încet, în sensul acelor de ceasornic, şi observaţi indicaţia voltmetrului. Realizaţi acelaşi lucru, dar în sens invers acelor de ceasornic. Care este diferenţa dintre cele două direcţii ale deplasării potenţiometrului?

Încercaţi să controlaţi potenţiometrul astfel încât să obţineţi o indicaţie stabilă a tensiunii. Ce tip de deplasare a potenţiometrului oferă cea mai stabilă indicaţie a tensiunii la bornele rezistorului de 1 MΩ?

2.11.4 Derivata unei funcţii în analiza matematică

O funcţie matematică ce reprezintă rata de variaţie a unei variabile faţă de o alta, poartă numele de derivată. Acest circuit simplu ilustrează conceptul de derivare prin producerea unei tensiuni de ieşire proporţionale cu variaţia tensiunii de intrare în raportul cu timpul. Prin urmare, acest circuit mai este cunoscut sub numele de circuit de diferenţiere.

La fel ca circuitul de mediere, circuitul de diferenţiere poste fi considerat un calculator analogic. Diferenţierea este o operaţie matematică mult mai complexă decât medierea, în special când este implementată într-un calculator digital. Acest circuit este aşadar un exemplu excelent al eleganţei circuitelor analogice în realizarea calculelor matematice. Desigur, se pot realiza circuite de diferenţiere mult mai precise prin combinarea reţelelor rezistor-condensator cu circuite electronice de amplificare. p>